В статье анализируется изгиб линейной части трубопровода, возникающий при ударных нагрузках. Предложена модель поперечных перемещений заглубленного трубопровода, которая позволяет оценить параметры импульсной ударной нагрузки.
Ключевые слова: воздействие взрывной нагрузки, нагрузки на трубопровод, поперечные перемещения трубопровода.
При воздействии ударной импульсной нагрузки на заглубленные сооружения (трубопровода) обычно выделяют три типа деформации:
изгиб линейной части;
продольное растяжение;
смятие цилиндрических диаметров линейной части.
В статье анализируется первый тип деформаций, возникающий чаще всего даже при сравнительно малых ударных нагрузках, если эпицентр её приложения попадает в критическую зону. Этот тип деформаций приводит при превышении допустимых нагрузок и достижению пределов текучести материала трубопровода к трещинообразованию в линейной части трубопровода и, как следствие, катастрофическим последствиям.
Рассматривая воздействие ударной волны в среде с преградой, на основе решения волнового уравнения в лагранжевых координатах, при известных начальных условиях получена приближенная формула, определяющая распределение давления по времени и длине заглубленного трубопровода:
, (1)
при начальных условиях:
u(x,0) = 0,
где - давление падающей волны на трубопроводе; — смещение (прогиб) трубопровода на расстоянии x от начала координат в момент времени t (при этом начало координат находится в точке пересечения оси трубопровода с перпендикуляром, опущенным из эпицентра ударной нагрузки на ось трубопровода); А — акустическое сопротивление грунта.
При создании моделипоперечных перемещений под воздействием ударной импульсной нагрузки предположим, что заглубленный трубопровод лежит на Винклеровом основании [1]. Дифференциальное уравнение в частных производных, описывающее вынужденные поперечные колебания (перемещения) трубопровода в грунте, с учетом соотношения (1) имеет вид:
, (2)
где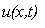 
- прогиб трубопровода на расстоянии 
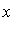от начала координат в момент времени t; I — осевой момент инерции сечения стержня (трубопровода); E — модуль упругости материала трубопровода; m1 — масса единицы длины трубопровода; 
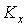- коэффициент постели; Dн — наружный диаметр трубопровода; Py — нагрузка, действующая по нормали к оси трубопровода.
Известно, что плоскостная задача решается проще, чем пространственная, учитывая, что трубопровод заглублен в грунт на 1...2 метра, рассмотрим задачу вычисления прогиба его линейной части на плоскости. Начало координат выберем в точке пересечения оси трубопровода и перпендикуляра, опущенного из эпицентра приложения ударной импульсной нагрузки на трубопровод, и вследствие симметрии будем рассматривать только его половину.
Зная, что на бесконечности функция u(x,t) иее производные до третьего порядка включительно должны обращаться в нуль, запишем граничные условия
, при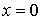 
. (3)
В начальный момент времени t=0 трубопровод находится в состоянии покоя, поэтому начальные условия примут вид:
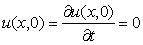
(4)
Для решения уравнения (2) с граничными (3) и начальными (4) условиями воспользуемся интегральным косинус-преобразованием Фурье, для чего слагаемые уравнения умножим на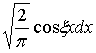
и проинтегрируем от нуля до бесконечности (здесь ξ — частотный коэффициент при переменной х):
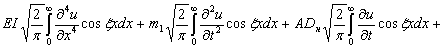
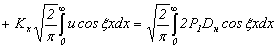
Для удобства последующих вычислений введем обозначения
; 
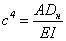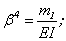
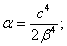
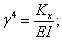
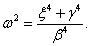
Обозначая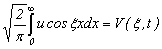 
, введем новую функцию от двух переменных — частотного коэффициента ξ и времени t. Интегрируем первое слагаемое 
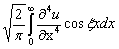последовательно по частям с учётом граничных условий (3). Получим для функции 
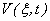обыкновенное дифференциальное уравнение
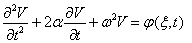, (5)
где
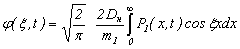(6)
с начальными условиями
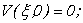
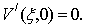(7)
Решение уравнения (5) содержит частное решение неоднородного дифференциального уравнения с постоянными коэффициентами и общее решение однородного линейного дифференциального уравнения:
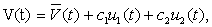
где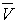 
(t)- некоторое частное решение, 
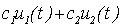— общее решение соответствующего однородного уравнения.
Общее решение однородного уравнения
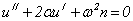(8)
будем искать в виде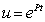 
(здесь P — некоторая постоянная, которую необходимо найти).
Вычислим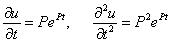 
. После подстановки в (8) и сокращения на неравное нулю 
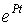, для определения P получим квадратное характеристическое уравнение:
.
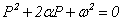Корни квадратного уравнения в зависимости от знака дискриминанта D уравнения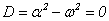 
являются вещественными или комплексными. Обозначим 
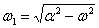. Если трение в грунте при смещении трубопровода большое, что определяется неравенством 
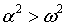, то характеристическое уравнение имеет вещественные корни 
.
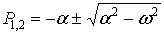Общее решение уравнения (8) имеет вид:
,
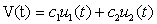где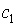 
и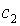 
некоторые постоянные, которые определяются исходя из начальных условий (7), следовательно:
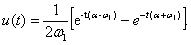
Если трение в грунте при смещении трубопровода незначительно, что определяется неравенством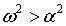 
, характеристическое уравнение имеет мнимые сопряжённые корни 
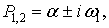где i — мнимая единица (i2 = -1). В этом случае общее решение дифференциального уравнения (8) имеет вид:
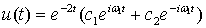
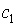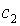Из начальных условий найдем значения констант и , получим:
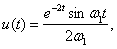
Для нахождения частного решения уравнения (5) применим функцию Грина, для этого нужно при начальных условиях (3) решить уравнение:
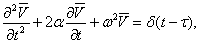(9)
Полагая, что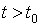 
и находится в следующих пределах 
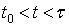, найдем решение однородного уравнения (8) при начальных условиях:
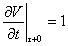(10)
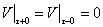(11)
Проинтегрируем (9) по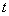 
от 
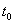до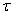 
, учитывая, что интегралы от конечных второго и третьего слагаемых в (9) равны нулю. Для общего решения уравнения (8) с использованием корней характеристического уравнения Р1 иР2 получим:
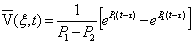
Это решение применимо для любых значений трения в грунте при смещении трубопровода.
Для последующих преобразований получим функцию Грина
.
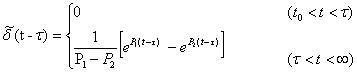Эта функция всюду непрерывна, кроме точки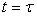 
, в которой происходит скачкообразное изменение. В этом случае решение уравнения (9) примет вид
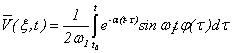(12)
Заметим, что для нагрузок, распределённых по времени и по длине трубопровода в общем случае решение задачи о вычислении его смещения является чрезвычайно сложным.
Экспериментальными исследованиями установлено, что для заглубленных в грунте магистральных трубопроводов имеет место только случай малого трения при смещении трубопровода, т. е.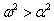 
.
На основе полученного решения (12) дифференциальной модели (2), а также литературных данных [2] можно утверждать, что при кратковременной ударной импульсной нагрузке, характерной для взрывов, имеет значение только величина и продолжительность импульса, что позволяет пренебречь формой импульса:
.
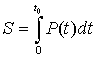Величина ударного импульса S, сообщаемого волной трубопроводу нами принята в качестве критерия разрушительной способности взрывной волны.
Проанализируем напряжения, возникающие от линейного смещения и изгибающих моментов в трубопроводе при действии сосредоточенного ударного импульса на рассматриваемой математической модели.
В начальный момент ударный импульс сообщает трубопроводу скорость u/0), но не вызывает его перемещения u(x,0). Следовательно
,
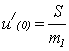где S= P1t0 — величина импульса; to — продолжительность действия импульса; m1 — масса единицы длины трубопровода.
Для анализа воздействия на трубопровод сосредоточенного ударного импульса, применим функцию Дирака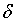 
(x). Тогда для функции давления, действующего на трубопровод, учитывая (6) получим:
.
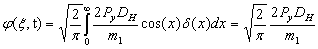Общее решение дифференциального уравнения (5) запишется в виде
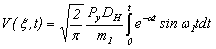. (13)
Обозначим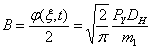 
. Интегрируя (13) от 0 до произвольного момента времени получаем:
при t ≤ t0
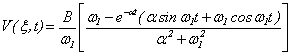; (14)
при t > t0
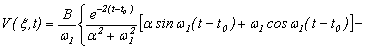
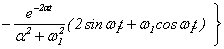. (15)
По формуле обращения косинус-преобразования Фурье получим смещение трубопровода u(x,t) в грунте:
при t ≤ t0
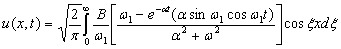(16)
при t > t0
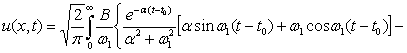
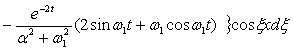. (17)
Вычисление в общем случае интегралов (16) и (17), описывающих прогиб трубопровода, представляет большие трудности. Поэтому рассмотрим решения для сосредоточенного импульса в сечении трубопроводов только в точке x=0 (в ней возникают наибольшие напряжения и деформации), что позволяет получить решение в виде удобных для практических применений формул, с использованием быстро сходящихся степенных рядов.
Для вычисления интегралов (16) и (17) выполним последовательные преобразования, включающие разложение подынтегральных функций в ряды по функциям Бесселя, разложение в ряды Тейлора и интегрирование полученных рядов. Окончательно получим формулу для определения смещения (прогиба) трубопровода в следующем виде:
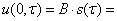
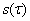
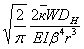. (18)
где s(τ) — функция времени, параметров трубопровода и среды, предварительно вычисляемая по следующей формуле:
,
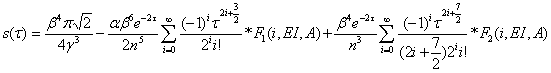здесь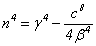 
, 
, 
, 
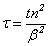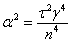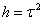— введенные обозначения, Fi — произведения гамма- и гипер-геометрических функций с определенными параметрами, зависящими от индекса суммирования, жесткости трубопровода и акустического сопротивления грунта, r — расстояние от эпицентра приложения взрывного импульса,W — приведенная мощность взрывного импульса, 
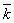- коэффициент, зависящий от свойства грунта.
При известных значениях нагрузки и коэффициентов, описывающих свойства грунтов формула (18) позволяет определить значение прогиба трубопровода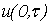 
после воздействия ударной импульсной нагрузки в произвольный момент времени 
.
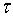Для определения максимальных изгибающих моментов в точке х=0 при взрывном импульсе математические выкладки аналогичны ранее изложенным. Опустив их, приведем соответствующую формулу для вычисления изгибающего момента:
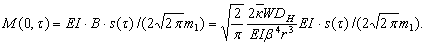(19)
Ряды, необходимые для вычисления выражений (18) и (19) сходятся быстро и для практических расчётов достаточно взять нескольких первых членов ряда. Эти формулы предназначены для вычисления деформаций от воздействия сосредоточенного ударного импульса.
Полученные в результате математического моделирования выражения для вычисления значений прогиба (18) и изгибающих моментов (19) для линейной части заглубленного в грунт трубопровода целесообразно сравнить с результатами натурных экспериментов. Их сопоставление показывает, что расчётные значения прогиба и изгибающих моментов несколько меньше экспериментальных. Это объясняется тем, что значения экспериментальных данных учитывают влияния рассеяния энергии взрыва в материале трубы и инерции основания. Из литературных источников известно, что разница в определении изгибающих моментов с учётом затухания энергии взрыва получается одного порядка с точностью вычислений [4]. Это объясняется тем, что изгибающий момент достигает своего максимума немного раньше смещений, при этом рассеяние энергии взрыва в материале трубопровода практически не влияет на величину его максимального значения.
Для практической оценки реакции линейной части трубопровода на воздействие взрывной нагрузки в зависимости от времени целесообразно ввести динамические коэффициенты изгибающего момента и смещения трубопровода. На рисунке 1 приведены зависимости динамических коэффициентов изгибающего момента (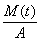
) и смещения трубопровода (
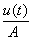) от продолжительности действия взрывной нагрузки (здесь А — акустическое сопротивление грунта). Как видно, поведение временных функций динамических коэффициентов аналогично.
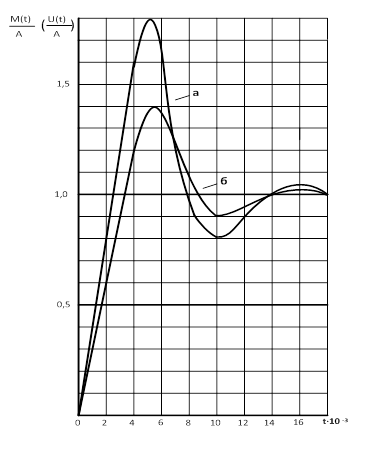
Рис. 1. Зависимости динамических коэффициентов от продолжительности действия взрывной нагрузки: а) для изгибающего момента; б) для смещения трубопровода.
Графики на рисунке 1 построены на основе данных проведенного эксперимента для нефтепродуктопровода диаметром 325 мм с толщиной стенки 9 мм, приведенной мощности взрывного импульса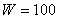 
кг в тротиловом эквиваленте и расстояния от эпицентра взрыва до нефтепродуктопровода 
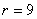м. Для расчетов используются коэффициенты среды 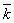= 30 и 
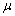= 3, зависящие от свойств грунтов, экспериментально определенные для широко распространенного глинистого песка в работе [3].
Из графика видно, что при мгновенном действии взрывного импульса трубопровод подвергается значительной нагрузке. С увеличением продолжительности действия взрывной нагрузки величина смещения из-за деформации трубопровода растёт и достигает своего максимума, который имеет значение 1,2…1,4, а для изгибающего момента — 1,6…1,8. Затем величины динамических коэффициентов сглаживаются (затухают) и уже при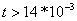 
с быстро приближаются к единице.
На рисунках 2 и 3 приведены графики распределения смещения и изгибающего момента по длине трубопровода для различных временных интервалов.
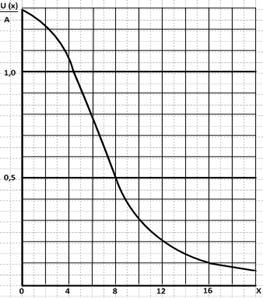
Рис. 2. График распределения динамического коэффициента прогиба (смещения) по длине трубопровода при продолжительности действия ударной нагрузки t0 = 3.10–3c
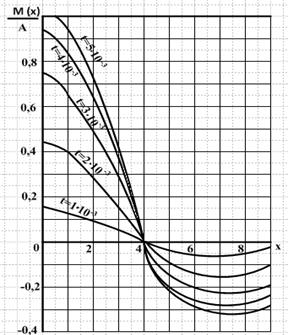
Рис. 3. График распределения динамического коэффициента изгибающего момента по длине трубопровода при различной продолжительности действия нагрузки.
Из графиков на рисунках 2 и 3 видно, что характер распределения изгибающего момента по длине нефтепродуктопровода практически не зависит от продолжительности действия нагрузки, при изменении длительности лишь меняются амплитуды прогибов линейной части и изгибающих моментов нефтепродуктопровода.
Предлагаемая модель поперечных перемещений заглубленного трубопровода является адекватной, результаты расчетов в достаточной степени согласуется с экспериментальными данными. Модель позволяет оценить критические ситуации и параметры импульсной ударной нагрузки, приводящие к значениям смещения (прогиба) линейной части, изгибающих моментов трубопровода и деформациям, при которых достигаются пределы текучести, возникает усталость материала оболочки и трещинообразование в линейной части трубопровода под воздействием импульсных ударных нагрузок.
Литература:
1. Ляхов Г. М. Основы динамики взрывов в грунтах и жидких средах. — М.:Недра, 1964
2. Садовский М. А. Механическое действие воздушных ударных волн по данным экспериментальных исследований// Сб.Физика взрыва. — М.: Изд-во АН СССР, 1952.
3. Мавлютов Р. М. Исследование поражаемости и напряженного состояния магистральных нефтепродуктопроводов при проведении взрывов: дисс. … канд.техн.наук. — Уфа: УГНТУ, 1971.
4. Взрывные явления. Оценка и последствия: в 2 кн./У.Бейкер, П.Кокс, П.Уэстайн [и др.]; пер. с англ. — М.: Мир, 1986.
