Известно, что при решении метрических задач, когда плоскость общего положения задается следами или линиями уровня, поставленные задачи значительно легче, удобнее и понятнее для студентов. Поэтому такие виды заданий плоскости общего положения мы в дальнейшем назовем «Базовым видом задания» плоскости общего положения.
Также известно, что на занятиях по начертательной геометрии, на примерах часто плоскости общего положения задаются в виде треугольника. И когда студенты при выполнении самостоятельных графических работ в задачах сталкиваются с заданием плоскости другого вида, т. е. проекциями трех точек, не лежащих на одной прямой или проекциями точки и (не проходящей через неё) прямой, или проекциями двух пересекающихся прямых или двумя параллельными прямыми, или проекциями плоских фигур (в виде четырех, пяти и шестиугольника или окружности, или кривой (замкнутой или разомкнутой), то у них возникают затруднения и психологический барьер, который они не всегда могут преодолеть самостоятельно. На наш взгляд причина появления такой проблемы у студентов заключается в недостаточности их теоретической базы.
Если проанализировать алгоритмы решения метрических задач, в большинстве случаев первым графическим действием является проведение от данной точки перпендикуляра к плоскости общего положения. И если плоскость задана не в базовом виде, то выполнение этого первого действия сходу невозможно. Когда плоскость задается в базовом виде, первое действие выполняется без проблем при условии перпендикулярности прямой к плоскости, вкратце описываемый следующим образом: р'h', p"f" и РН║h', РV║f".
Наши исследования показали, что причиной затруднения студентов при выполнении первого графического действия, является то, что в нем скрывается проведение горизонтали и фронтали заданной плоскости. Т. е. в алгоритмах при решении метрических задач в первом графическом действии спрятано преобразование вида заданной плоскости в базовый вид.
Поэтому мы считаем, что методологически целесообразно выделить из первого действия алгоритма решения метрических задач приведение заданной плоскости общего положения из произвольного вида задания в удобно решаемый базовый вид, как самостоятельное графическое действие.
В данной статье речь идёт об усовершенствовании алгоритмов решения метрических задач и модернизации различных видов задания плоскости общего положения, преобразуя их чертеж в оптимальный вид, т. е. преобразуя в базовый вид задания плоскости общего положения.
Известно, что метрические задачи (1), как определение расстояния от точки S до плоскости Q(h∩f) решаются алгоритмом c тремя графическими действиями по следующему алгоритму (Рис.1.):
 (1)
(1)

Рис. 1.
На основании этого алгоритма также решаются задачи (2) определения расстояния между двумя параллельными плоскостями и (3) расстояния между скрещивающимися прямыми линиями. Для этого во второй задаче выбирается произвольная точка, лежащая в заданной плоскости, и таким образом задача решается так же как первая с тремя действиями. В третьей задаче через одну из двух скрещивающихся прямых проводится параллельная плоскость к другой прямой и выбирается произвольная точкаво второй прямой. Таким образом, третья задача преобразуется как первая задача и решается также тремя действиями.
Если в задачах плоскость общего положения задается в произвольном виде, то необходимо отдельно выделить выполнение преобразования их в базовый вид, т. е. преобразование их с линиями уровня этих плоскостей (иначе задачи не решаются), как отдельное графическое действие (рис.2).

Рис. 2.
Таким образом, алгоритм решения метрических задач на определение расстояния от точки до плоскости, состоит из трех графических действий. С точки зрения методики студенты затрудняются при выполнении первого графического действия алгоритма. Поэтому мы считаем необходимым усовершенствование алгоритма решения как метрических, так и позиционных задач начертательной геометрии. Чтобы сохранить установившееся за годы количество графических действий алгоритмов, мы будем считать преобразование плоскости общего положения в базовый вид задания 0-нулевым алгоритмом.
Поэтому, когда в задачах плоскость общего положения задаётся в произвольном виде, то целесообразно в начале решения какой-либо задачи начертательной геометрии, преобразить их в базовый вид, т. е. линиями уровня этих плоскостей. В результате этого задачи решаются более простым путем и с минимальным количеством графических манипуляций.
Выше мы упоминали о том, что усовершенствование алгоритма решения также даёт преимущество при решении позиционных задач. В качестве доказательства этого заключения мы рассмотрим пример конкретного решения задачи, как построения следов плоскости, заданной в виде Р(h∩f) базовой (Рис.4), и в виде треугольника АВС (Рис.5).
Известно, что такие задачи решаются по следующему алгоритму:
- Строится горизонтальный след фронтали f плоскости P, М(М',М");
- Через точку М' проводится прямая параллельная горизонтальной проекции горизонтали плоскости h', и тем самым строится горизонтальный след РН плоскости Р.
- Строится фронтальный след горизонтали h плоскости P, N(N',N");
- Через точку N" проводится прямая параллельная фронтальной проекции фронтали плоскости f", и строится фронтальный след РV плоскости Р. Символическими обозначениями этот алгоритм можно перезаписать так:
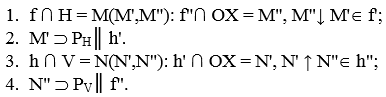 (2)
(2)
Чтобы в дальнейшем ссылаться на этот алгоритм, назовем его вторым алгоритмом. В задачах на построение следов плоскости, если их задать различными способами, т. е. в виде треугольника АВС, то необходимо преобразить её в базовый, как на рисунке 5, с применением второго алгоритма, задача решается значительно более легко и удобно, т. е. с тремя графическими действиями:
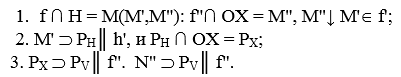
Если эту задачу решать без преобразования, т. е. как в задаче на Рис. 4, то задача решается пятью манипуляциями:
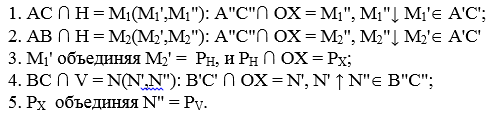

Если точка схода следов окажется за пределами чертежа, то для построения фронтального следа необходимо построить ещё одну точку. В таком случае задача решается шестью манипуляциями.
Такой творческий подход при решении позиционных задач дает следующие преимущества:
- Сравнивая выполненное количество графических манипуляций на рис.4. и рис.5. можно установить, что число манипуляций при решении задач уменьшается на 40 % — 50 %; если плоскость задана как базовая задания (т. е. линиями уровня).
- Для построения следов плоскости достаточно построить следы линий уровня, найти по одной их точек, т. к. вторая их точек является несобственной точкой по направлению линии уровня. Именно поэтому: РН║ h' и РV║ f";
- Не всегда точки следов плоскости находятся в пределах чертежа как на рис.2, и выходят за пределы чертежа, что создаёт некоторое неудобство в построении. Изображая плоскость линиями уровня, мы легко избавимся от таких затруднений;
- Изображая заданный произвольный вид плоскости общего положения в вид базового задания, можно установить первый алгоритм как единый алгоритм решения задач по построению следов плоскости, состоящий из четырех манипуляций.
Таким образом, упрощается и становится более удобным не только решение поставленной выше задачи, но и всех возможных метрических задач, когда искомые точки выходят за пределы чертежа
Применение нулевого алгоритма, т. е. преобразования плоскостей общего положения в вид базового задания, в учебном процессе при решении метрических и позиционных задач, на 16% повысило показатели успеваемости по начертательной геометрии у студентов Ташкентского государственного педагогического университета в 2014–2015 учебном году.
Литература:
- Н. А. Антипина и др. Начертательная геометрия. Часть 1. «Издательство Томского политехнического университета», 2011. стр. 35–36.
- Сайидаҳмедов Н. С., Абдурахимов С. А. “Педагогическая мастерство и технология”. Монография, -Т., 2009,Б. 203–207стр.
- Рихсибаев Т. “Методология преподавания предметов инженерной графики”. –Т., 2011, 30–35 стр.
- Рихсибоаев У. Т. Решение метрических задач новым прямо угольным способом в начертательной геометрии. Кандидатская диссертация, –Т., 2007, 58–69 стр.
- Нурматов Э., Рихсибаев Т. Определение удобного вида задания плоскости общего положения при решении задач. “Инновационные технологии”. Сборник материаллов научно-прктической конференции. –Т., ТДПУ, 2014, 189 стр.







