В настоящей статье определяется положения плоскостей общего положения пересекающих поверхностей 2-го порядка (на примере трёхосного эллипсоида) по эллипсу на перёд заданной площади.
In persisting article is defined positions of the planes of the general provisions crossing surfaces 2-go order (on example of the ellipsoid with three axises) on ellipse on before given area.
В инженерной практике наряду с задачей нахождения положения секущих плоскостей, содержащих конические сечения заданных параметров, нередко может возникнуть необходимость определения на теле, ограниченном поверхностями 2-го порядка, плоских сечений, имеющих наперед заданную площадь.
Как известно, из всех поверхностей 2-го порядка только площадь эллиптических сечений выражается через их параметры. В связи с этим исследуем только положение плоскостей, пересекающих тело, ограниченное поверхностью 2-го порядка, по эллипсу, площадь которого наперед задана и равна S.
Площадь эллипса S через его параметры характеризуется формулой
S=π·an·bn, (1)
где an и bn-полуоси эллипса, которые в данном случае неизвестны.
При изменении значения одной из полуосей вторая изменяется обратно пропорционально первой, удовлетворяя наперед заданному знчению S. При такой постановке вопроса задача остается неопределенной, так как можно построить множество плоскостей, пересекающих тело, ограниченное поверхностью 2-го порядка, по эллипсу наперед заданной площади S.
Исследуем задачу нахождения положения плоскости, пересекающей тело, ограниченное поверхностью 2-го порядка общего вида, по эллипсу наперед заданной площади S, при условии, что искомая плоскость параллельна плоскости Θ общего положения и пересекает заданную поверхность по эллипсу [3.135 ст.]. Следует отметить, что при такой постановке задачи нахождение полуосей вспомогательного эллипса существующими методами усложняется. Поэтому можно допустить следующие упрощения.
Вращаем рассматриваемую систему вокруг оси симметрии заданной поверхности до такого положения, пока плоскость Θ окажется фронтально-проецирующей. Тогда поверхность принимает новый фронтальный очерк.
Если пересечь поверхность ф2 в повернутом положении фронтально-проецирующей плоскостью, параллельной заданной плоскости, то получим сечение в виде эллипса, сопряженными полудиаметрами которого будут аi и bi. Эти полудиаметры можно определить, используя теорему подобия эллипсов. Площадь одного из эллипсов известна, площадь второго эллипса лежит в плоскости, которая параллельна Θ и проходит через специально выбранную точку рассматриваемой поверхности.
Используя теорему об отношении площадей родственных фигур, можно легко доказать, что площадь эллипса равна
Si=πai1bi1sinα1, (2)
где α1-угол между сопряженными диаметрами эллипса. Исходя из этого, для площади данного сечения получим значение [1.18 ст.].
Sn= πan1bn1sinα1, (3)
Совместно решая (2) и (3) относительно an1 и bn1, находим выражение для сопряженных полудиаметров искомого сечения в повернутом положении
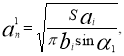
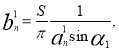 (4)
(4)
По найденным параметрам an1 и bn1 по формулам (4) легко определить положение искомой плоскости, пересекающей тело по заданной площади сечения S.
Для построения фронтального очерка поверхности в повернутом положении проводим касательные к горизонтальному очерку поверхности в повернутом положении по направлению проекционной связи. По фронтальной проекции этих точек и по некоторым неподвижным точкам, используя свойства очерковых кривых, строим фронтальный очерк поверхности в повернутом положении.
На примере трехосного эллипсоида. Чтобы определить положение плоскости, пересекающей трехосный эллипсоид по заданной площади S, вращаем его вокруг вертикальной оси до тех пор, пока заданная плоскость θ не станет фронтально-проецирующей. При таком повороте оси A1B1 и C1D1 займут положение A11B11и С11D11 (рис. 1), соответственно изменится и фронтальный очерк трехосного эллипсоида. Для построения фронтального очерка после поворота достаточно провести касательную прямую по направлению проекционной связи к повернутому положению горизонтального очерка заданного трехосного эллипсоида. При помощи родственного соответствия, не строя горизонтального очерка, находим точки касания. Для этого окружность с радиусом О11В11 и O1D11 принимаем родственной эллипсу с полуосями.
Ось родства является прямая- A11B11, пара родственных точек- D11и111 [2.с.193]. Построим направление прямой O1211, отвечающей направлению касательной. Проведем диаметр O131 окружности, перпендикулярный к O1211. Диаметрам O1211 и O131соответствуют сопряженные диаметры эллипса O121 и O1311. Точка 311, соответствующая точке 31, является точкой касания касательной к горизонтальному очерку эллипса, совпадающей с вертикальной линией связи. Определив фронтальные проекции этих точек и используя точки I2II2, лежащие на оси вращения, получим возможность построить фронтальный очерк трехосного эллипсоида в повернутом положении.
Затем проводим через центр эллипсоида вспомогательную плоскость Г2//θ2. Плоскость Г2 пересечет эллипсоид по эллипсу, сопряженными полудиаметрами которого являются ОЕ1 и OF (рис.1). Натуральную величину ОЕ1 определяем методом вращения, а OF-исходя из родства эллипса и окружности.
Благодаря подобию между вспомогательным и искомым сечениями сопряженные полудиаметры искомого сечения опишем выражением
![]() и
и 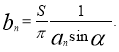 (5)
(5)
Полученные параметры (5) представим графически (рис.2) Проведем две пересекающиеся прямые m0 и n0 под углом α, затем построим следующие отрезки [4.325 ст.]: В0С0, измеряющий OF sin α; C0A0, пропорциональный трем отрезкам, имеющим длину S/π; ОЕ и В0С0; α1= A01D01 как среднее геометрическое отрезков длиной C0A01 и 1. Построим также отрезок b1= A0E0, пропорциональный трем отрезкам длиной S/π, 1 и A01D01, где A01D01= α1sinα.
Для построения положения искомой плоскости от точки О1 отложим на отрезке О1 Е1 величину отрезка а1 и найдем соответствующие проекции 51 и 52 точки 5 (см.рис.1). Построим прямую n2, сопряженную направлению Θ2. Через точки 52 и 521 проведем прямую, параллельную n2 и пересекающуюся с очерком трехосного эллипсоида в повернутом положении, по эллипсу заданной площади S. Обратным поворотом находим искомые плоскости Q и Q1 (плоскость Q1 на рис.1 не показана) общего положения.
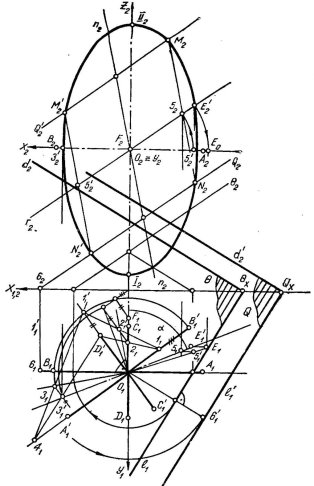
Рис. 1.
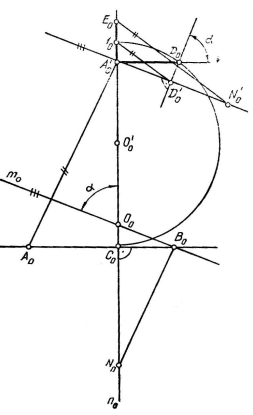
Рис. 2.
Литература:
- Н. Ф. Четверухин «Проективная геометрия» издательство «Просвещение», М.1949
- Н. С. Кузнецов «Начертательная геометрия» издательство «Высшая школа» М.1969
- Ш. К. Муродов «Эллиптическое сечение тел, ограниченных поверхностями 2-го порядка, по заданной площади». В сборнике «Прикладная геометрия и инженерная графика». Вып. V Киев: Будiвельник 1967
- Отажанов Р. К. «Геометрик ясашлар», Ташкент «Ўқитувчи нашриёти»,1965







