Внедрение интеллектуальных систем управления, в частности, предиктивных регуляторов, позволяет существенно снизить энергопотребление за счет оптимизации режимов работы установок на основе математических моделей. Точность таких моделей, особенно их динамической составляющей, становится критическим фактором успеха. Данная работа представляет собой практический этап проекта «Предиктивное управление энергопотреблением на базе ПЛК и ИИ в отечественной среде разработки ALTA IDE», выполняемого в рамках конкурса «Сириус.Лето». Целью этапа являлась экспериментальная идентификация и верификация динамической модели типового элемента системы — апериодического звена первого порядка. Работа актуальна не только в прикладном ключе для конкретного проекта, но и как пример полного цикла получения и обработки реальных данных с использованием доступного отечественного аппаратно-программного комплекса. Экспериментальные исследования проводились на лабораторном стенде с применением программируемого логического контроллера ОВЕН ПЛК-210 и среды разработки ALTA IDE . В ходе пяти опытов снимались кривые разгона по каналу «положение регулирующего органа — расход». Последовательная обработка данных (нормировка, синхронизация, фильтрация) и строгий критерий валидации позволили отобрать три пригодные для анализа переходные характеристики. Для идентификации параметров модели (коэффициента усиления и постоянной времени) к каждой кривой независимо применялся метод наименьших квадратов. Сравнение результатов, полученных для трех различных экспериментов, стало основным методом проверки адекватности модели и воспроизводимости результатов.

Полученные результаты не только формируют надежную основу для синтеза контура управления в среде ALTA IDE, но и демонстрируют эффективную методологию перехода от «сырых» экспериментальных данных к верифицированной математической модели, что представляет ценность для образовательных и прикладных инженерных задач.

Для верификации выбранной модели апериодического звена была выполнена процедура её параметрической идентификации. На Рисунках 1–2 представлены результаты сопоставления расчётной модели с экспериментальными данными для каждого из трёх валидных опытов. Как визуально видно на графиках, теоретические кривые демонстрируют высокую степень соответствия реальным переходным процессам, что является первым свидетельством адекватности модели. Количественная оценка этого соответствия и метод, позволивший его достичь, подробно описаны в следующем разделе.

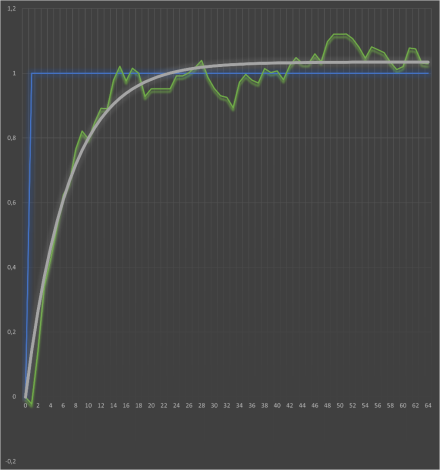
Рис. 1. Опыт 2, модель и данные

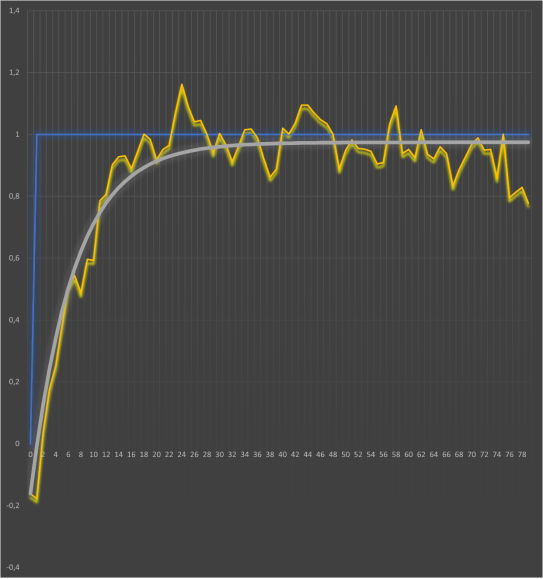
Рис. 2. Опыт 3, модель и данные

Таблица 1

Перемещение РО в экспериментах

В ходе серии из пяти экспериментов фиксировалась реакция расхода (номинальное значение 125 т/ч, максимальное 250 т/ч) на ступенчатое изменение положения РО. Первичный анализ заключался в визуализации всех «сырых» экспериментальных данных на одном графике, что позволило оценить разброс и наличие помех.

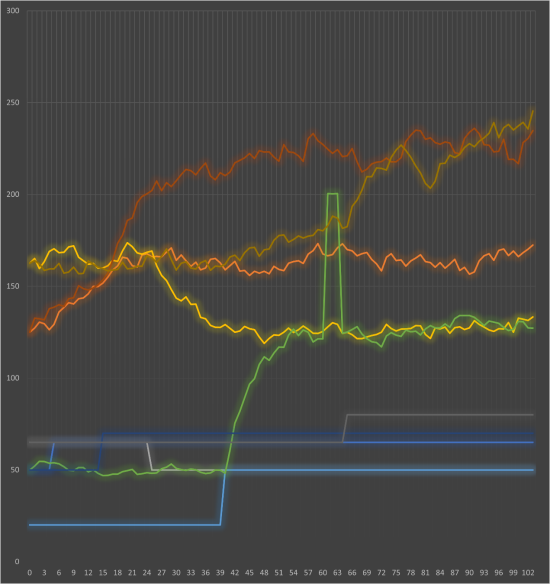
Рис. 3. Сырые экспериментальные данные

Для последующего анализа и сравнения с теоретической моделью данные были подвергнуты процедуре нормировки. Положение РО и значение расхода были приведены к безразмерному виду в диапазоне от 0 до 1. Для этого все значения положения РО были пересчитаны относительно их диапазона изменения, а значения расхода — поделены на максимальную величину (250 т/ч). Кроме того, для преобразования кривых разгона в стандартные переходные характеристики (реакцию на единичное ступенчатое воздействие) показания расхода были отнесены к величине приложенного возмущения (разнице между конечным и начальным положением РО в каждом опыте). Особенностью второго эксперимента было отрицательное возмущение (снижение положения РО). Для удобства сравнения с другими опытами данная кривая была развернута умножением на -1, что позволило работать с однонаправленными переходными процессами.

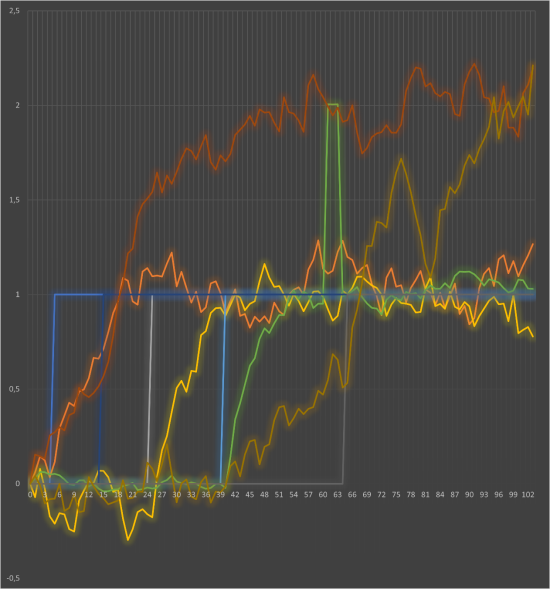
Рис. 4. Нормировка

Для корректного сравнительного анализа и последующего усреднения данные всех экспериментов были синхронизированы по времени. Момент подачи ступенчатого воздействия (изменения положения РО) для каждой кривой был принят за новый нулевой момент времени. Таким образом, все переходные процессы на графике начинаются из одной точки, что позволяет наглядно сопоставлять их динамику, форму и установившиеся значения независимо от реального хронологического порядка проведения опытов. Данная процедура является стандартным этапом подготовки экспериментальных данных при идентификации динамических объектов.

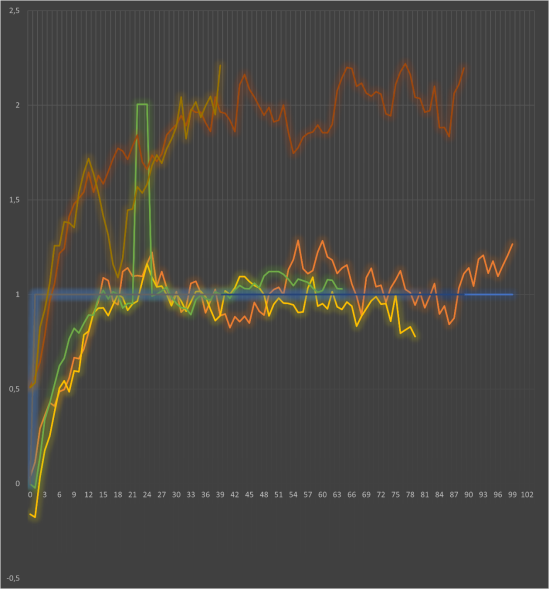
Рис. 5. Синхронизация переходных процессов по времени

Для обеспечения достоверности результатов был проведен критический анализ качества всех пяти полученных кривых разгона на предмет их пригодности для идентификации модели. В результате два эксперимента были исключены из дальнейшего рассмотрения. В первом из них наблюдался значительный дрейф измеряемой величины еще до момента приложения тестового ступенчатого воздействия, что указывало на нестационарное состояние объекта и нарушало базовое условие проведения эксперимента. Второй эксперимент был отбракован, поскольку его динамические характеристики качественно отличались от остальных данных даже в «сыром» виде.

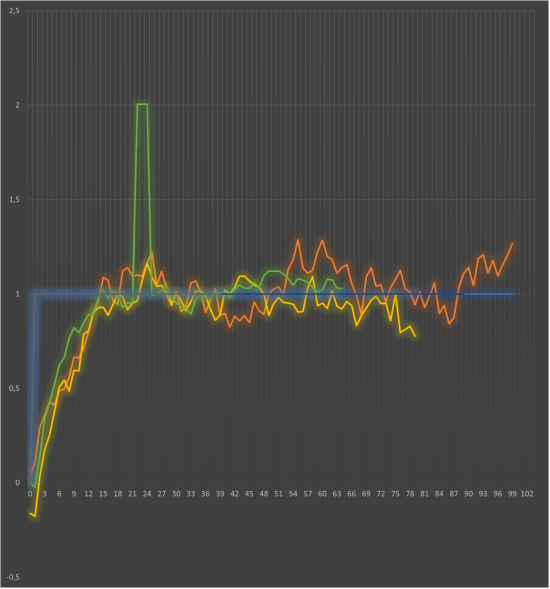
Рис. 6. Оставшиеся три эксперимента

Консультация с персоналом, обслуживающим установку, подтвердила гипотезу о том, что эти данные были ошибочно получены с другого технологического канала и были предоставлены в том числе для проверки корректности методики валидации экспериментальных данных. После исключения этих опытов для анализа остались три кривые, соответствующие одному и тому же объекту.

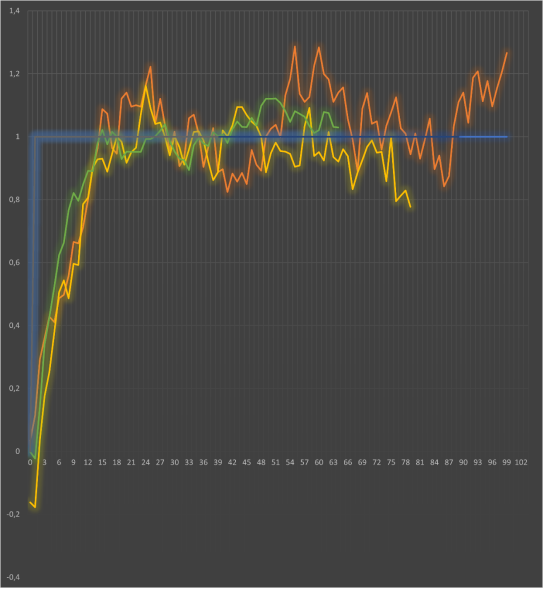
Рис. 7. Устранили выброс в третьем эксперименте

В одном из трех выбранных экспериментов были зафиксированы три аномальных выброса значений. Для сохранения целостности переходного процесса данные в этих точках были скорректированы с помощью линейной интерполяции между соседними достоверными отсчетами. Таким образом, итоговая выборка для построения модели была сформирована на основе трех проверенных и очищенных переходных характеристик. Полученный набор обработанных переходных характеристик служит основой для следующего этапа работы: расчёта передаточных функций, анализа динамических параметров и, что наиболее важно, сравнения результатов, полученных из «зашумлённых» реальных данных, с параметрами эталонной модели объекта.

Качественный анализ очищенных и нормированных переходных характеристик показал, что их форма соответствует реакции стандартного динамического звена — апериодического звена первого порядка . Его математическая модель описывается дифференциальным уравнением, а в терминах передаточной функции характеризуется двумя параметрами: коэффициентом усиления и постоянной времени . Для точного количественного определения этих параметров по экспериментальным данным был применен метод наименьших квадратов [1], Суть метода в данном случае заключалась в подборе таких значений и , при которых расчетная кривая, описываемая уравнением апериодического звена, наилучшим образом аппроксимировала все точки экспериментальных данных. Процедура МНК была последовательно применена к каждой из трех проверенных переходных характеристик.

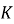
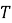
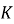
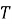
Полученные оценки параметров для всех трех экспериментов показали хорошую сходимость, что свидетельствует о воспроизводимости результатов и корректности выбранной структуры модели.

Таблица 2

Результаты

Обсуждение результатов

Применение метода наименьших квадратов к трём независимым переходным характеристикам позволило получить оценки параметров, представленные в Таблице 2. Незначительный разброс значений (коэффициент усиления K от 0.97 до 1.06, постоянная времени T от 7.26 до 8.47 с) объясняется наличием шума в исходных данных и неидеальностью ступенчатого воздействия. Важно отметить, что оценки, полученные для разных по величине и направлению возмущений, демонстрируют хорошую количественную и качественную сходимость. Это свидетельствует о том, что объект в исследуемом диапазоне может быть адекватно описан линейной моделью. Для построения итоговой модели, удобной для синтеза регулятора, на основании кластера полученных оценок были приняты округлённые значения: коэффициент усиления K = 1 (безразмерный), постоянная времени T = 8 с.

Вывод и дальнейшие планы

Проведённая работа продемонстрировала полный цикл перехода от натурного эксперимента к верифицированной математической модели объекта управления в рамках проекта по созданию системы предиктивного управления. На отечественном программно-аппаратном комплексе (ПЛК ОВЕН ПЛК-210, среда ALTA IDE) были получены кривые разгона, после чего выполнена комплексная обработка данных, включающая нормировку, синхронизацию, валидацию и очистку от аномалий. Ключевым результатом этапа стала успешная идентификация параметров апериодического звена методом наименьших квадратов по трём независимым экспериментальным кривым. Сходимость полученных оценок (K ≈ 1, T ≈ 8 с) подтвердила адекватность выбранной структуры модели и воспроизводимость результатов.

Полученная передаточная функция W(s) = 1/(8s+1) является надёжной основой для синтеза системы управления. На следующем этапе планируется: реализация и настройка ПИД-регулятора в среде ALTA IDE на основе этой модели; проведение испытаний замкнутой системы; сравнение её переходных процессов с исходными экспериментальными данными для окончательной проверки точности идентификации. Таким образом, работа закладывает фундамент для внедрения алгоритмов прогнозирующего управления, демонстрируя эффективность связки отечественного инструментария ALTA IDE с классическими методами теории автоматического управления.

Литература:

1. Андрюшин, А. В. Управление и инноватика в теплоэнергетике: учебное пособие / А. В. Андрюшин, В. Р. Сабанин, Н. И. Смирнов. — Москва: МЭИ, 2016. — 392 с. — ISBN 978–5–383–01037–2.