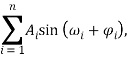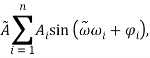Актуальность
Одним из видов сигналов, существующих в природе, является звуковой сигнал, который представляет из себя передачу информации посредством звуковых волн (гудок, свисток арбитра и т. п.). На протяжении изучения звуковых сигналов были выделены следующие их формы: прямоугольная, синусоидная, треугольная и пилообразная. Форма звуковой волны задаётся функцией, значение которой является амплитудой сигнала в определённый момент времени. Различными комбинациями базовых волн возможно получить и другие формы звуковой волны. Так же, чтобы добиться разнообразия, можно использовать различные звуковые фильтры, которые могут изменять сигнал.
Музыка представляет из себя одну из областей, где активно используется генерация звуковых сигналов. Однако существующие синтезаторы не позволяют сгенерировать любую форму звуковой волны, что является определенным барьером на пути освоения мира электронной музыки. Актуальность данной работы в том, что создав универсальный параметр формы звукового сигнала, который позволит получить любую звуковую волну, можно собрать универсальный синтезатор звуковых сигналов. Такой синтезатор сможет значительно обогатить и улучшить мир электронной музыки и не только.
Синтезаторы звука используют множества различных способов получения определённого звука. Самый распространённый метод это «сэмплинг», где звук не синтезируется, а воспроизводится, то есть в синтезаторе заранее хранятся образцы различных звуков. Этот метод не даёт возможности получить любой звук, так как даже если удастся записать почти все нужные звуки, то в памяти синтезатора они могут не уместиться. И даже если со временем и появятся соответствующие объемы памяти для этих звуков, помимо них существует огромное множество тех, что не встречаются в человеческой природе и могут быть воспроизведены только при соответствующем оборудовании, которое на данный момент не всегда удобно в эксплуатации. Чтобы найти подход к разрешению этой проблемы, было принято решение рассмотреть такое явление, как аддитивный синтез.
Аддитивный синтез был основан на теоретических работах математика и физика Жана Батиста Жозефа Фурье. Этот синтез основывается на возможности получения любого звука при помощи смешивания необходимого количества синусоидальных сигналов [1, с. 12].
Аддитивный синтез весьма сложен для реализации из-за необходимости отдельного контроля амплитуды и частоты каждой гармоники, которых даже несложный тембр насчитывает десятки, поэтому этот метод не совсем подходит для генерации любой формы волны. Однако с помощью него можно разложить звуковую волну на необходимые параметры, которые в свою очередь позволят найти для них некую общую функцию.
В настоящий момент для того, чтобы сгенерировать волну с какой-нибудь особой формой, необходимо вручную редактировать профиль волны, использовать комбинации различных звуковых фильтров, изменять параметры каждой гармоники и производить множество других операций. Но даже эти методы не дадут возможность сгенерировать любую звуковую волну искусственного происхождения.
Ранее уже предпринимались попытки создать музыкальный синтезатор, который будет генерировать практически любой звук. Примером такого синтезатора являлся АНС, сконструированным советским инженером Евгением Мурзиным в 1958 году, который также использовал принцип аддитивного синтеза [1, с. 12].
Но для генерации определенных звуковых волн в синтезаторе АНС использовался долгий и многоступенчатый процесс предварительной подготовки. С тех пор достижения в этой области не сильно продвинулись. Несмотря на это, возможности данного синтезатора по-прежнему вызывают интерес среди композиторов.
Целью данной работы является разработка генератора звуковых сигналов аддитивного синтеза с использованием универсального параметра, что позволит сгенерировать любую форму сигнала. Это в свою очередь позволит оптимизировать работу с генерацией звука в рамках аддитивного синтеза.
Для достижения цели были решены следующие задачи:
‒ Найдена универсальная функция для генерации звуковой волны любой формы;
‒ Составлена матрица, каждый столбец, которой является сигналом;
‒ Вынесены в качестве коэффициентов функции такие важные параметры сигнала, как амплитуда и частота.
Разложение сигнала вряд
Любую функцию можно представить в виде суммы синусоид. Т. е. любой сигнал можно разложить в ряд Фурье [3]. В общем виде ряд представлен в формуле (1), где n — количество синусоид; ![]() – амплитуда i-го сигнала;
– амплитуда i-го сигнала; ![]() – частота i-го сигнала, Гц;
– частота i-го сигнала, Гц; ![]() – начальная фаза i-го сигнала.
– начальная фаза i-го сигнала.
|
|
(1) |
Ряд можно представить в виде набора трёхмерных векторов ![]() Каждый вектор будет хранить в себе параметры амплитуды, частоты и начальной фазы синусоиды. Перебирая все возможные варианты наборов таких векторов, можно перебрать все возможные варианты форм сигналов. Но проблема в том, что в этом наборе векторов будут попадаться одинаковые сигналы по своей форме, но с разной частотой или амплитудой. Поэтому запишем ряд Фурье в другом виде, представленном в формуле (2), где
Каждый вектор будет хранить в себе параметры амплитуды, частоты и начальной фазы синусоиды. Перебирая все возможные варианты наборов таких векторов, можно перебрать все возможные варианты форм сигналов. Но проблема в том, что в этом наборе векторов будут попадаться одинаковые сигналы по своей форме, но с разной частотой или амплитудой. Поэтому запишем ряд Фурье в другом виде, представленном в формуле (2), где ![]() – абсолютная амплитуда,
– абсолютная амплитуда, ![]() ;
; ![]() — абсолютная частота,
— абсолютная частота, ![]() , (так как 22кГц предел для человеческого слуха), Гц;
, (так как 22кГц предел для человеческого слуха), Гц; ![]() ;
; ![]() ;
; ![]() .
.
|
|
(2) |
Используя формулу (2) можно избавиться от лишних наборов векторов, ограничив при этом допустимые диапазоны амплитуды и частоты, нужный набор при этом можно будет умножить на вектор ![]() с абсолютными параметрами. Таким образом используя уже три параметра, такие как: амплитуда, частота и набор векторов, отвечающих за форму волны, то есть этот набор можно уже назвать тем самым параметром формы волны, возможно получить любой звуковой сигнал.
с абсолютными параметрами. Таким образом используя уже три параметра, такие как: амплитуда, частота и набор векторов, отвечающих за форму волны, то есть этот набор можно уже назвать тем самым параметром формы волны, возможно получить любой звуковой сигнал.
Генерация всех существующих форм сигналов
Теперь используя формулы, полученные выше, для генерации всех форм сигналов остаётся только перебрать все существующие вектора. Вектора можно представить в виде обычных чисел, например, в диапазоне от 000 000 000 до 999 999 999, где каждые три цифры это один из параметров синуса в ряде Фурье. Массив таких чисел и будет содержать в себе всё нужную информацию о форме волны. Все возможные варианты набора вышеописанных чисел будут нести в себе информацию о всех существующих формах сигнала.
В итоге мы получаем матрицу, где столбец — это сумма синусоид, а элемент каждая отдельно взятая синусоида, составляющая волну. Параметр формы волны представляет из себя номер столбца в этой матрице. Задача сводится к тому, чтобы сгенерировать такую матрицу и упорядочить её элементы. Размер матрицы nxm, где n — количество синусоид в волне (увеличивая n, увеличивается точность формы сигнала и увеличиваются различные варианты форм), m — количество возможных форм сигнала при выбранном n. Эту же матрицу можно представить и как лексикографическую последовательность.
В качестве примера был взят упрощенный диапазон от 0 до 2 (k=2), где количество синусоид в волне равно 3. Перечислим в лексикографическом порядке все последовательности длины n=3, состоящие из чисел 0, 1, 2.
{(0, 0, 0), (0, 0, 1), (0, 0, 2), (0, 1, 0), (0, 1, 1), (0, 1, 2), (0, 2, 0), (0, 2, 1), (0, 2, 2),
(1, 0, 0), (1, 0, 1), (1, 0, 2), (1, 1, 0), (1, 1, 1), (1, 1, 2), (1, 2, 0), (1, 2, 1), (1, 2, 2),
(2, 0, 0), (2, 0, 1), (2, 0, 2), (2, 1, 0), (2, 1, 1), (2, 1, 2), (2, 2, 0), (2, 2, 1), (2, 2, 2)}.
Исключим последовательность, состоящую из одних нулей, а также каждую такую последовательность, элементы которой образуют такое же сочетание с повторениями, как и элементы какой-либо другой последовательности, стоящей слева от нее. В результате имеем следующее упорядоченное множество:
{(0, 0, 1), (0, 0, 2), (0, 1, 1), (0, 1, 2), (0, 2, 2), (1, 1, 1), (1, 1, 2), (1, 2, 2), (2, 2, 2)}.
Можно видеть, что оно является упорядоченным лексикографически множеством последовательностей, представляющих собой все различные лексикографически упорядоченные n-элементные сочетания с повторениями чисел от 0 до k.
Покажем, как, зная номер элемента такого множества, можно найти сам элемент. То есть, увеличив диапазон и задав только лишь номер столбца (параметр формы волны), можно получить любую форму сигнала.
Пусть дан номер N последовательности длины n, состоящей из чисел 0,..., k. В качестве примера рассмотрим случай, когда пусть n=3, k=4, N=10, т. е. нужно найти последовательность длины n=3, состоящую из 0, 1, 2, 3, 4, по его номеру, равному 10.
1. Данному номеру последовательности N сопоставляется последовательность длины n+k, состоящая из n нулей и k единиц. Т. е., в примере номеру N сопоставляется последовательность длины 7, состоящая из 3 нулей и 4 единиц. Это делается следующим образом:
1.1. Номер N сравнивается с С(n+k-1, k) (эта величина считается по формуле: С(a, b) = a! / (b!*(a-b)!)). Если N<С(n+k-1, k), то первым знаком последовательности будет 0; если N>=С(n+k-1, k), то первым знаком последовательности будет 1.
В нашем примере N=10 сравнивается с С(6, 4)=15. Т. к. 10<15, то первым знаком последовательности будет 0. Считается N_1. Эта величина будет равна N, если полученный знак — ноль, или равна N-C(n+k-1, k), если полученный знак — единица. В нашем примере N_1=N=10.
1.2. Следующий шаг повторяется до тех пор, пока не найдено всё слово.
В начале шага мы имеем начало слова длины j, в котором содержится e единиц, и величину N_j. В примере после выполнения первого шага мы имеем начало слова (0) длины j=1, которое содержит e=0 единиц, и величину N_1=10.
Величина N_j сравнивается с С(n+k-j-1, m-e). Если N_k<С(n+k-j-1, m-e), то (j+1)-м знаком последовательности будет 0; если N_j>=С(n+k-j-1, m-e), то (j+1)-м знаком последовательности будет 1.
В нашем примере N_1 сравнивается с С(5, 4)=5. Т. к. 10>5, то вторым знаком последовательности будет единица. Считается N_{j+1}. Эта величина будет равна N_j, если полученный знак — ноль, или равна N_j-C(n+k-j-1, m-e), если полученный знак — единица.
В нашем примере N_2=10–5=5. Возвращаемся к началу шага. В примере: имеем начало слова (0, 1) длины 2, в котором содержится e=1 единица, и N_2=5. Для нахождения третьего знака слова N_2 сравнивается с С(4, 3)=4. Т. к. N_2>C(4, 3), то третьим знаком слова будет единица, N_3=5–4=1.
Имеем начало слова (0, 1, 1) длины 3, в котором содержится e=2 единиц, и N_3=1. Для нахождения четвертого знака N_3 сравнивается с С(3, 2)=3. Т. к. N_3<c(3, 2),="" <="" n_4="N_3=1." p="" будет="" знаком="" ноль,="" слова="" то="" четвертым="">
Имеем начало слова (0, 1, 1, 0) длины 4, в котором содержится e=2 единиц, и N_4=1. Для нахождения пятого знака N_4 сравнивается с С(2, 2)=1. Т. к. N_4=C(2, 2), то пятым знаком слова будет единица, N_5=i_4-С(2, 2)=0.
Имеем начало слова (0, 1, 1, 0, 1) длины 5, в котором содержится e=3 единиц, и N_5=0. Для нахождения шестого знака N_5 сравнивается с С(1, 1)=1. Т. к. N_5<c(1, 1),="" <="" p="" будет="" знаком="" ноль.="" то="" шестым="">
Имеем начало слова (0, 1, 1, 0, 1, 0). Т. к. мы ищем слово длины 7, в котором три нуля и четыре единицы, то можно видеть, что по началу однозначно определяется искомое слово (0, 1, 1, 0, 1, 0, 1).
2. Найденной последовательности длины n+k, состоящей из n нулей и k единиц, ставится в соответствие искомая последовательность длины n, состоящая из чисел 0,..., k. Это осуществляется следующим образом:
2.1. Заменим в полученной последовательности нули на единицы и наоборот.
В нашем примере получаем (1, 0, 0, 1, 0, 1, 0). Заменяем серии единиц (последовательности единиц, идущих подряд) на числа, представляющие собой длины этих серий.
В нашем примере последовательности (1, 0, 0, 1, 0, 1, 0). ставится в соответствие последовательности (1, 0, 0, 1, 0, 1, 0). В нашем примере полученная последовательность совпадает с исходной, поэтому приведем еще несколько примеров: последовательности (0, 1, 1, 1, 0, 0, 0) ставится в соответствие (0, 3, 0, 0, 0); последовательности (0, 1, 1, 0, 1, 0, 0) ставится в соответствие (0, 2, 0, 1, 0, 0).
2.2. Вычеркиваем по одному нулю из каждой серии нулей, кроме той, с которой последовательность начинается, и той, которой последовательность кончается.
В нашем примере последовательность заканчивается серией нулей длины 1. Она остается без изменений. Также в последовательности содержится серия нулей длины 2 и серия нулей длины 1. Вычеркивая по одному нулю из каждой получаем последовательность (1, 0, 1, 1, 0).
2.3. Пронумеруем элементы полученной последовательности от 0 до k. Поставим в соответствие ей последовательность чисел от 0 до k, заменяя k-й элемент серией длины, равной значению этого элемента, чисел k.
В нашем примере 0-й элемент равен 1, он заменяется серией длины 1 чисел 0, т. е. последовательностью (0). 1-й элемент равен 0, он заменяется серией длины 0 чисел 1, т. е. пустой последовательностью. 2-й элемент равен 1, он заменяется серией длины 1 чисел 2, т. е. последовательностью (2). 3-й элемент равен 1, он заменяется серией длины 1 чисел 3, т. е. последовательностью (3). 4-й элемент равен 0, он заменяется серией длины 0 чисел 4, т. е. пустой последовательностью.
Получаем искомую последовательность (0, 2, 3). Это и будет искомой последовательностью, имеющей номер N=10.
Заключение
- Найден универсальный параметр, отвечающий за форму сигнала, изменяя который становится возможным получение любой формы волны. Для этого остаётся выразить зависимость в полученной матрице через формулы. Это необходимо для того, чтобы матрицу не приходилось строить вновь и вновь, а просто рассчитывать весь столбец, то есть рассчитывать параметры каждой составляющей синусоиды сигнал.
- После выведенной в математическом виде зависимости станет возможным написание универсального синтезатора с тремя параметрами: частота, амплитуда и форма сигнала. Такой более простой и универсальный в эксплуатации синтезатор даст возможность генерации любых звуковых сигналов с максимальной практичностью.
Литература:
- Мурзин, Е. А. О природе и закономерностях эстетического восприятия и путях становления музыки электронной и цвета [Текст] / Е. А. Мурзин. — М.: Издательский дом «Композитор», 2008. — 340 с.
- Преобразование Фурье: [Электронный ресурс]: [веб-сайт] — Режим доступа: https://ru.wikipedia.org/wiki/Преобразование_Фурье 25.05.2015
- Ряд Фурье: [Электронный ресурс]: [веб-сайт] — Режим доступа: https://ru.wikipedia.org/wiki/Ряд_Фурье 07.06.2016
- Комбинации Элементов: [Электронный ресурс]: [веб-сайт] — Режим доступа: https://en.wikipedia.org/wiki/Combination#/media/File