Цифровой синтезатор частот



В статье рассматриваются алгоритмы формирования цифровых гармонических сигналов, приведены критерии сравнения реализации алгоритмов, результаты синтеза в ПЛИС.

Ключевые слова: цифровой синтезатор частот, DDS, ПЛИС.

Цифровой синтезатор частоты (DDFS — direct digital frequency synthesis) или прямой цифровой синтез Direct Digital Synthesis, DDS) выдает на выходе цифровые отсчеты заданной частоты f, является составной частью квадратурного демодулятора (рис.1) либо используется для формирования аналогового сигнала в схеме генератора (рис.2).

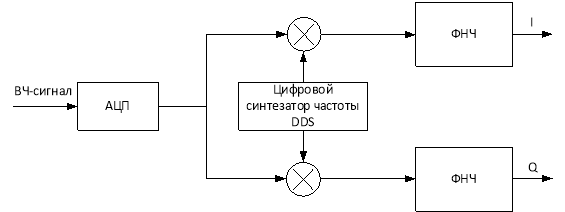
Рис. 1. Квадратурный демодулятор

Рис. 2. Генератор сигнала

Для реализации DDFS существует несколько способов:

1) Алгоритм прямого цифрового синтеза (DDS) — наиболее часто используемый алгоритм, название которого совпадает с названием группы методов синтеза цифровых сигналов, включает аккумулятор фазы и преобразователь фазы в цифровой код, представляющий собой блок ПЗУ. Входным параметров является шаг приращения адреса памяти, определяющий значение частоты входного сигнала. Достоинством алгоритма, определяющим его широкое использование, является простота реализации, возможность изменения генерируемой частоты при сохранении неразрывности фазы. Недостаток — большие затраты памяти, характеристики синтезатора зависят от объема ПЗУ. В генераторах гармонических сигналов для уменьшения затрат в памяти хранят 1/4 значений синуса на одном периоде.

2) Методы тригонометрических преобразований — представление аргумента в виде суммы нескольких слагаемых, тем самым уменьшая диапазон вычисляемого аргумента и сокращая объем памяти. В [1] приведены характеристики реализаций этого подхода [2–5].

3) Методы аппроксимации — разложения функции в ряд Тейлора [6]. Сокращение памяти в этом методе и методе тригонометрических преобразований реализуется за счет дополнительных операций умножения и сложения.

4) Алгоритмы CORDIC [1, 7–8] используют алгоритм в режиме «поворот». Реализация алгоритма включает выполнение сложения/ вычитания, операцию сдвига и одну операцию умножения. Характеристики сигнала зависят от разрядности, числа каскадов (итераций) алгоритма.

5) Комбинация 1 или 3 методов и алгоритма 4 [1], позволяет уменьшить затраты памяти.

6) Алгоритм на рекурсивном фильтре [9–10]. Достоинство алгоритма — отсутствие затрат памяти, недостаток — зависимость характеристик сигнала от разрядности данных.

Выбор реализации DDS зависит от области применения устройства, энергопотребления. Основным критерием является возможность использования памяти, если нет принципиальных ограничений на объем используемой памяти, то используется 1 вариант.

Следующим критерием является минимизация аппаратных затрат при условии выполнения требований к качеству сигнала, которое оценивается по значению параметра SFDR (динамический диапазон, свободный от паразитных составляющих) [1, 6, 8, 11]. В современных приложениях устройство должно обеспечивать значение SFDR не менее 70 дБ. Для каждого алгоритма необходимо определить параметры, обеспечивающие заданное SFDR, примеры зависимости параметров алгоритма CORDIC приведены, например, в [11], в этой работе приведено выражение, связывающее параметры алгоритма (разрядность данных, разрядность аргумента и число каскадов) со значением SFDR. При отсутствии аналитических зависимостей требуемые параметры находятся моделированием.

Для сравнения аппаратных затрат на реализацию цифрового синтезатора частот были реализованы алгоритмы DDS, Cordic и алгоритм на рекурсивном фильтре (RF). Результаты синтеза для ПЛИС xc6vlx75t-3-ff484 приведены в таблице.

Таблица

Аппаратные затраты на реализацию алгоритмов

Алгоритм	DDS	CORDIC	RF
Number of Slice Register	48	2218	50
Number of Slice LUT	78	2325	75
Number of fully used LUT-FF pairs	42	2190	50
Number of Block RAM/ FIFO	1
Number of BUFG/BUFG CTRLs		32	1
Number of DSP48E1s	2		1

Параметры реализованных алгоритмов:

— DDS — разрядность данных 20, разрядность накопителя фазы — 18 (1024 отсчета в памяти);

— CORDIC — – разрядность данных 24, количество каскадов -26, данные — синус/ косинус;

— RF — разрядность данных 25, разрядность множителя — 18.

Реализация алгоритма CORDIC не требует использования блоков памяти и блоков DSP48, при этом формируются отсчеты синуса и косинуса, для реализации схем DDS и RF необходимо практически одинаковое число элементов, за исключением блоков памяти.

Следовательно, алгоритм генерации дискретного синусоидального сигнала на базе рекурсивного фильтра может быть использован для реализации в базисе ПЛИС для относительных частот сигнала в диапазоне 0,001243–0,24999 частоты дискретизации.

Литература:

1. Maher, J. Direct Digital Frequency Synthesizer with CORDIC Algorithm and Taylor Series Approximation for Digital Receivers / Jridi Maher, Alfalou Ayman. — Текст: непосредственный // European Journal of Scientific Research, EuroJournals. — 2009. — № 30(4). — PP. 542–553. https://hal.archives-ouvertes.fr/hal-00516790/PDF/ejsr_30_4_03.pdf
2. Sunderland, D. A. CMOS/SOS frequency synthesizer LSI circuit for spread spectrum communication / D. A. Sunderland, R. A. Strauch, S. S. Wharfield, T,Peterson — Текст: непосредственный // IEEE Journal of Solid-State Circuits. — 1984. — № vol.19 no. 4,. — PP. 497–506.
3. Essenwanger K. A., Sine output DDSs. A survey of the state of the art/ K. A. Essenwanger, V. S. Reinhardt and A.Zarowin //Proceeding Int. Frequancy control symp. — 1998. — PP. 370–378.
4. Nicholas, H. T. A 150-MHz direct digital synthesizer in 1.25 mm CMOS with 90-dBc spurious performances / T,Nicholas,III,and,H H. — Текст: непосредственный // IEEE Journal of Solid-State Circuits. — 1991. — № vol.26 no. 12. — PP. 1959–1969.
5. Kent, G. W. A high purity high speed direct digital synthesizer/ G. W. Kent and N. H. Sheng // Porceding Int. Frequancy control symp., — 1995. — pp. 207–211.
6. Cordesses, L. Direct Digital Synthesis: A Tool for Periodic Wave Generation (Part 1) / Cordesses Lionel. — Текст: непосредственный // IEEE Signal processing magazine. — 2004. — PP. 50–54. https://www.stepfpga.com/doc/_media/dsp_dds1.pdf
7. Kang, C. Y. An analysis of the CORDIC algorithm for direct digital frequency synthesis / Y,Kang,and,E,E C, Jr,.. — Текст: непосредственный // in Proc. IEEE Int. Conf. Application-Specific Systems, Architectures and Processors. — 2002. — № 6. — С. 111–119.
8. Дайнеко, Д. Реализация CORDIC-алгоритма на ПЛИС. / Дайнеко Дмитрий. — Текст: электронный // Компоненты и технологии. — 2011. — № 12. — С. 36–46. https://kit-e.ru/wp-content/uploads/2011_12_36.pdf
9. Al-Ibrahim, M. M. A simple recursive digital sinusoidal oscillator with uniform frequency spacing / M. M. Al-Ibrahim. — Текст: непосредственный // ISCAS 2001–2001 IEEE International Symposium on Circuits and Systems, Conference Proceedings. — 2001. — № 2, art. no. 921164. — С. 689–692.
10. Калыгин, Г. О. Цифровой генератор сигналов / Г. О. Калыгин. — Текст: непосредственный // Молодой ученый. — 2020. — № № 32 (322). — С. 30–33.
11. Пузырёв, П. И. Исследование влияния параметров алгоритма CORDIC в составе цифрового смесителя на динамический диапазон, свободный от паразитных составляющих / П. И. Семенов, К.Пузырёв. — Текст: непосредственный // Омский научный вестник. — 2017. — № № 1 (15). — С. 80–84.