Математическая модель свободнопоршневого двигателя Стирлинга
Авторы: Бобылев Александр Викторович, Зенкин Владимир Александрович
Рубрика: Энергетика
Опубликовано в Техника. Технологии. Инженерия №1 (3) январь 2017 г.
Дата публикации: 04.01.2017
Статья просмотрена: 2158 раз
Библиографическое описание:
Бобылев, А. В. Математическая модель свободнопоршневого двигателя Стирлинга / А. В. Бобылев, В. А. Зенкин. — Текст : непосредственный // Техника. Технологии. Инженерия. — 2017. — № 1 (3). — С. 22-27. — URL: https://moluch.ru/th/8/archive/46/1862/ (дата обращения: 20.09.2024).
Представлено описание термодинамической модели двигателя Стирлинга, приведены основные уравнения и результаты моделирования 57-икиловаттной свободно-поршневой установки бета-типа.
Ключевые слова: двигатель Стирлинга, математическая модель, термодинамическая модель, свободнопоршневой двигатель, двигатель Била
Двигатель Стирлинга — это машина, работающая по замкнутому термодинамическому циклу, в которой циклические процессы сжатия и расширения происходят при различных уровнях температур, а управление потоком рабочего тела осуществляется путем изменения его объема [1]. В настоящее время они применяются, когда необходима длительная работа энергетической установки без обслуживания, в случае жестких требований по многотопливности, или, например, по шуму. Данные двигатели применяют в солнечной энергетике, подводном флоте, различной спецтехнике. В космической отрасли двигатели Стирлинга возможно использовать в качестве энергетических установок, работающих на атомных или радиоизотопных источниках тепла.
Для задач проектирования в настоящее время применяют математические модели различного уровня сложности. Эти модели необходимы для того, чтобы подобрать параметры двигателя, получить его предварительные характеристики исходя из заданных требований.
Их разработка и реализация в настоящее время активно продолжается как в России [4], [5], [6], так и за рубежом [7], [8], [9].
В качестве первого этапа расчетного анализа двигателя Стирлинга широко применяются термодинамические математические модели, разработке которой и посвящена настоящая статья.
Математическая модель описывает рабочий процесс свободнопоршневого двигателя Стирлинга. За основу была выбрана установка, разрабатываемая NASA [3] в качестве генератора электрической энергии на космических станциях, приводимая в работу от ядерного реактора либо от солнечных батарей. Рабочее тело — гелий. Схема свободнопоршневого двигателя Стирлинга представлена на рис. 1.
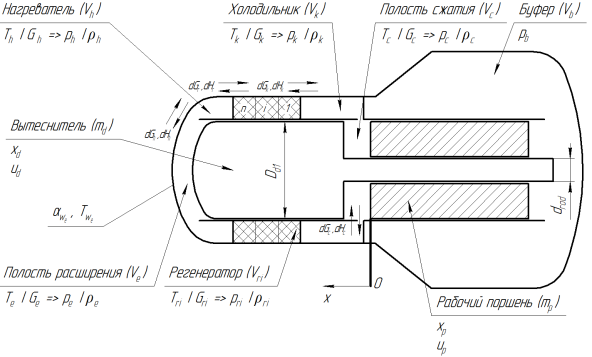
Рис. 1. Схема свободнопоршневого двигателя Стирлинга
При формулировке математической модели был принят ряд допущений:
‒ рабочая область разбита на восемь объемов:
‒ полость сжатия, ![]() ;
;
‒ холодильник, ![]() ;
;
‒ регенератор, разбитый на три объема, ![]() ;
;
‒ нагреватель, ![]() ;
;
‒ полость сжатия, ![]() ;
;
‒ буферная полость, ![]() ;
;
‒ газ, находящийся внутри каждого из объемов, описывается первым законом термодинамики для открытых систем;
‒ движение вытеснителя и рабочего поршня — свободное, описано вторым законом Ньютона;
‒ тепловое состояние деталей конструкции не изменяется во времени и предполагается заданным;
‒ теплообмен в теплообменниках и регенераторе описывается законом Ньютона-Рихмана;
‒ утечки через зазоры отсутствуют;
‒ перетекание газа из объема в объем рассчитывается по квазистационарным соотношениям.
Схема сил, действующих на вытеснитель и рабочий поршень представлена на рис. 2.
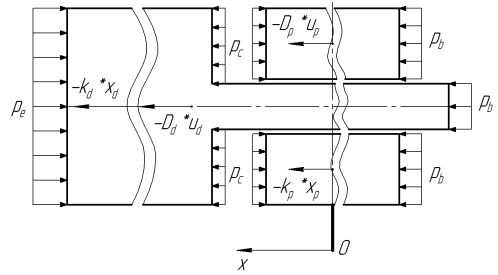
Рис. 2. Схема приложения сил к вытеснителю и рабочему поршню
Модель двигателя описывается восемнадцатью интегрируемыми уравнениями, которые приведены ниже:
1) Уравнение перемещения вытеснителя
![]() ,
,
где ![]() – перемещение вытеснителя, м;
– перемещение вытеснителя, м;
![]() – скорость вытеснителя, м/с.
– скорость вытеснителя, м/с.
2) Уравнение перемещения рабочего поршня
где ![]() – перемещение рабочего поршня, м;
– перемещение рабочего поршня, м;
![]() – скорость рабочего поршня, м/с.
– скорость рабочего поршня, м/с.
3) Уравнение скорости вытеснителя
![]() ,
,
где![]() ,
,![]() ,
, ![]() — давления в буферной полости, полости сжатия и полости расширения соответственно, Па;
— давления в буферной полости, полости сжатия и полости расширения соответственно, Па;
![]() ,
, ![]() ,
, ![]() — площади штока, вытеснителя со стороны полости сжатия и вытеснителя со стороны полости расширения соответственно,
— площади штока, вытеснителя со стороны полости сжатия и вытеснителя со стороны полости расширения соответственно, ![]() ;
;
![]() – коэффициент демпфирования вытеснителя, кг/с;
– коэффициент демпфирования вытеснителя, кг/с;
![]() – коэффициент жесткости пружины вытеснителя,
– коэффициент жесткости пружины вытеснителя, ![]() ;
;
![]() – масса вытеснителя, кг.
– масса вытеснителя, кг.
4) Уравнение скорости рабочего поршня
где ![]() – площадь рабочего поршня,
– площадь рабочего поршня, ![]() ;
;
![]() – коэффициент демпфирования рабочего поршня, кг/с;
– коэффициент демпфирования рабочего поршня, кг/с;
![]() – коэффициент жесткости пружины рабочего поршня,
– коэффициент жесткости пружины рабочего поршня, ![]() ;
;
![]() – масса рабочего поршня, кг.
– масса рабочего поршня, кг.
5) Уравнения расхода рабочего тела через полость сжатия
![]() ,
,
где 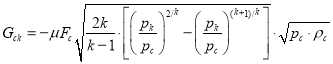 , если
, если ![]() –расход через проходное сечение между полостью сжатия и холодильником, кг/с. Остальные расходы через проходные рассчитываются аналогично;
–расход через проходное сечение между полостью сжатия и холодильником, кг/с. Остальные расходы через проходные рассчитываются аналогично;
![]() — давление в холодильнике, Па;
— давление в холодильнике, Па;
![]() – плотность рабочего тела в полости сжатия,
– плотность рабочего тела в полости сжатия, ![]() ;
;
![]() — показатель адиабаты;
— показатель адиабаты;
6) Уравнение расхода рабочего тела через холодильник
![]()
7) Уравнение расхода рабочего тела через первую полость регенератора
![]()
8) Уравнение расхода рабочего тела через вторую полость регенератора
![]()
9) Уравнение расхода рабочего тела через третью полость регенератора
![]()
10) Уравнение расхода рабочего тела через нагреватель
![]()
11) Уравнение расхода рабочего тела через полость расширения
![]()
12) Уравнение внутренней энергии для полости сжатия
![]() ,
,
где ![]() — поток энтальпии через проходное сечение, Дж/с;
— поток энтальпии через проходное сечение, Дж/с;
![]() – удельная теплоемкость рабочего тела при постоянном давлении.
– удельная теплоемкость рабочего тела при постоянном давлении.
13) Уравнение внутренней энергии для холодильника
![]() ,
,
где ![]() – площадь поверхности теплообмена в соответствующей полости,
– площадь поверхности теплообмена в соответствующей полости, ![]() ;
;
![]() – коэффициент теплоотдачи в соответствующей полости,
– коэффициент теплоотдачи в соответствующей полости, ![]() ;
;
![]() – температура поверхности теплообмена, К;
– температура поверхности теплообмена, К;
14) Уравнение внутренней энергии для первой полости регенератора
![]()
15) Уравнение внутренней энергии для второй полости регенератора
![]()
16) Уравнение внутренней энергии для третьей полости регенератора
![]()
17) Уравнение внутренней энергии для нагревателя
![]()
18) Уравнение внутренней энергии для полости расширения
![]()
Значения констант и коэффициентов для рассматриваемого двигателя были приняты, основываясь на [3].
В качестве среды разработки использовался программный комплекс Matlab [2]. Модель была составлена в соответствии с функциональной парадигмой программирования, для интегрирования дифференциальных уравнений был применен метод Рунге-Кутты четвертого порядка.
Результаты математического моделирования
В результате интегрирования системы уравнений, описанных выше, были получены характеристики рабочего процесса двигателя, представленные в таблице 1.
Таблица 1
Интегральные характеристики свободнопоршневого двигателя Стирлинга
|
Эффективная мощность, кВт |
57,4 |
|
Частота, Гц |
94,3 |
|
Средняя температура в нагревателе, К |
894,9 |
|
Средняя температура в холодильнике, К |
469 |
|
Среднее давление, МПа |
13,8 |
|
Амплитуда рабочего поршня, мм |
15,1 |
|
Амплитуда вытеснителя, мм |
8,1 |
|
Фаза между вытеснителем и поршнем, градус |
61,1 |
|
Фаза между вытеснителем и давлением, градус |
74,7 |
|
Фаза между поршнем и давлением, градус |
13,6 |
Мгновенные значения параметров моделируемой системы приведены на рисунках ниже. PV-диаграмма представлена на рис. 3. На рис. 4 представлен график движения поршней, на рис. 5–6 представлены графики параметров газа в теплообменниках.
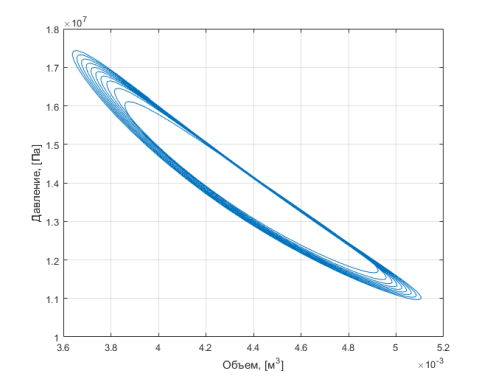
Рис. 3. PV-диаграмма двигателя
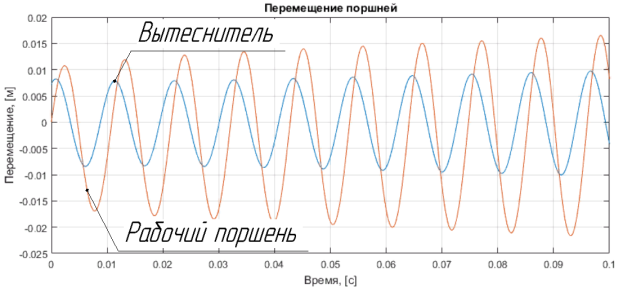
Рис. 4. График перемещения вытеснителя и рабочего поршня в зависимости от времени
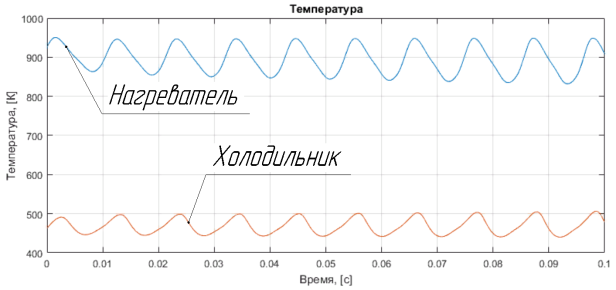
Рис. 5. Температура в холодильнике и нагревателе в зависимости от времени
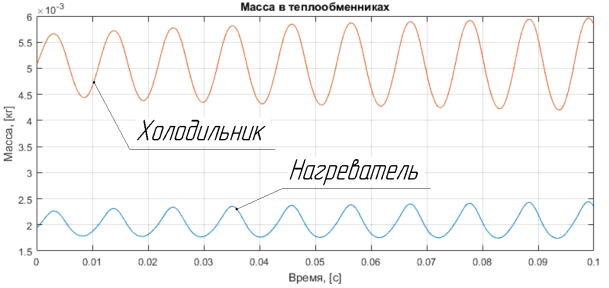
Рис.6. Масса рабочего тела в холодильнике и нагревателе в зависимости от времени
Заключение
В результате проделанной работы была создана математическая модель свободнопоршневого двигателя Стирлинга, которая может быть использована для первичной оценки показателей двигателя, анализа его рабочего процесса, решения вопросов управления и функционирования в рамках надсистем.
Литература:
1. Уокер, Г. Двигатели Стирлинга/Сокр. пер. с англ. Б. В. Сутугина и Н. В. Сутугина.–М.: Машиностроение, 1985.–408 с., ил.
2. Программный комплекс MATLAB. Режим доступа: http://matlab.ru (дата обращения 21.12.16).
3. Langlois, Justin L. R. Dynamic computer model of a Stirling space nuclear power system. Trident Scholar project report no. 345.–Annapolis: US Naval Academy, 2006.
4. Светлов В. А., Ефимов С. И., Иващенко Н. А., Сячинов А. В. Методика определения параметров теплообмена во внутреннем контуре двигателя Стирлинга// “Двигатель — 97”. Материалы международной научно-технической конференци. — М.: Изд. МГТУ. — 1997.
5. Веревкин М. Г. Метод комплексного теплового и конструкторского расчета термомеханического генератора // Известия ВУЗов. Машиностроение, 2004. —№ 10. -С.33–37.
6. Абакшин А. Ю. Численное моделирование процессов тепло- и массобмена в цилиндрах двигателя с внешним подводом теплоты / А. Ю. Абакшин, Г. А. Ноздрин, М. И. Куколев // Научно-технические ведомости СПбГПУ, 2012. –№ 2–2(1477). —с.164–167.
7. Kouji Kumagai, Hiroyuki Yamasaki. Performance Prediction of Linear Stirling Power Generator with Two Displacers// 6th International Energy Conversion Engineering Conference (IECEC) (28–30 July 2008, Cleveland, Ohio).
8. Kwanchai Kraitong. Numerical modelling anddesign optimisation of Stirling engines for power production// World Renewable Energy Congress 2011 (8–13 May 2011, Linkoping, Sweden).
9. Hang-Suin Yang, Chin-Hsiang Cheng. A Nonlinear Non-dimensional Dynamic Model for Free Piston Thermal-lag Stirling Engine// Energy Procedia (December 2014)
Ключевые слова
математическая модель, термодинамическая модель, двигатель Стирлинга, свободнопоршневой двигатель, двигатель БилаПохожие статьи
Математическая модель расчета двухтактных двигателей...
Математическая модель описывает рабочий процесс свободнопоршневого двигателя Стирлинга. – температура поверхности теплообмена, К; — температура рабочего тела, К. 14) Уравнение внутренней энергии для первой полости регенератора. Пути снижения потерь на...
Моделирование насосных ходов в картере одноцилиндрового...
Математическая модель свободнопоршневого двигателя Стирлинга.
Математическая модель расчета двухтактных двигателей... Моделирование рабочего процесса поршневого двигателя началось вместе с созданием данного типа двигателей.
Анализ конструктивных решений по созданию транспортной...
Математическая модель свободнопоршневого двигателя...
Математическая модель для расчёта утечек через поршневые... В двигателях внутреннего сгорания для уплотнения зазора между поршнем и гильзой используются компрессионные поршневые кольца.
Математическая модель для расчёта утечек через поршневые...
Потеря массы рабочего тела ведёт к уменьшению давления и, как следствие, работы цикла.
В частности, можно отметить, что свободнопоршневые двигатели внутреннего сгорания (ДВС) превосходят
Математическая модель расчета двухтактных двигателей...
Перспективы применения роторно-поршневых двигателей
Математическая модель расчета двухтактных двигателей... Моделирование рабочего процесса поршневого двигателя началось вместе с
Разработка научно-технических решений прямого преобразования тепловой энергии двигателей внутреннего сгорания в электрическую.
Обзор математических моделей рабочих процессов газового...
Большинство использующихся в отечественной практике моделей интегрально описывают поведение рабочего тела в цилиндре.
Ключевые слова: камера сгорания, газовый двигатель, программный комплекс, отработавшие газы, моделирование, математическая модель...
Компьютерное моделирование гидравлических систем
Построена математическая модель типовой гидравлической системы, Построение и
‒ насос для подачи рабочей жидкости из бака и создания давления в системе
Нестационарный режим моделируется обыкновенными дифференциальными уравнениями [10]
Энергетические установки воздухонезависимых подводных...
рабочее тело, подводной аппарат, тепловой двигатель, гребной электродвигатель, перекись водорода, забортная вода, единый двигатель, горячая полость, главный холодильник, абсорбционная колонка.
Похожие статьи
Математическая модель расчета двухтактных двигателей...
Математическая модель описывает рабочий процесс свободнопоршневого двигателя Стирлинга. – температура поверхности теплообмена, К; — температура рабочего тела, К. 14) Уравнение внутренней энергии для первой полости регенератора. Пути снижения потерь на...
Моделирование насосных ходов в картере одноцилиндрового...
Математическая модель свободнопоршневого двигателя Стирлинга.
Математическая модель расчета двухтактных двигателей... Моделирование рабочего процесса поршневого двигателя началось вместе с созданием данного типа двигателей.
Анализ конструктивных решений по созданию транспортной...
Математическая модель свободнопоршневого двигателя...
Математическая модель для расчёта утечек через поршневые... В двигателях внутреннего сгорания для уплотнения зазора между поршнем и гильзой используются компрессионные поршневые кольца.
Математическая модель для расчёта утечек через поршневые...
Потеря массы рабочего тела ведёт к уменьшению давления и, как следствие, работы цикла.
В частности, можно отметить, что свободнопоршневые двигатели внутреннего сгорания (ДВС) превосходят
Математическая модель расчета двухтактных двигателей...
Перспективы применения роторно-поршневых двигателей
Математическая модель расчета двухтактных двигателей... Моделирование рабочего процесса поршневого двигателя началось вместе с
Разработка научно-технических решений прямого преобразования тепловой энергии двигателей внутреннего сгорания в электрическую.
Обзор математических моделей рабочих процессов газового...
Большинство использующихся в отечественной практике моделей интегрально описывают поведение рабочего тела в цилиндре.
Ключевые слова: камера сгорания, газовый двигатель, программный комплекс, отработавшие газы, моделирование, математическая модель...
Компьютерное моделирование гидравлических систем
Построена математическая модель типовой гидравлической системы, Построение и
‒ насос для подачи рабочей жидкости из бака и создания давления в системе
Нестационарный режим моделируется обыкновенными дифференциальными уравнениями [10]
Энергетические установки воздухонезависимых подводных...
рабочее тело, подводной аппарат, тепловой двигатель, гребной электродвигатель, перекись водорода, забортная вода, единый двигатель, горячая полость, главный холодильник, абсорбционная колонка.







