Математическая модель для расчёта утечек через поршневые кольца



Цель работы — получение аналитической зависимости для определения эффективного проходного сечения поршневых колец при расчёте утечек газа в четырёхтактном двигателе.

Для достижения поставленной цели необходимо решить ряд задач:

– разработать математическую модель для расчета состояния газа в цилиндре и объёмах между кольцами четырёхтактного двигателя внутреннего сгорания с учётом утечек через поршневые кольца;

– подобрать значения эффективных площадей проходного сечения колец для двигателей с различными диаметрами цилиндра по известным экспериментальным данным;

– получить эмпирическую формулу для расчета эффективной площади проходного сечения поршневых колец от диаметра цилиндра.

В двигателях внутреннего сгорания для уплотнения зазора между поршнем и гильзой используются компрессионные поршневые кольца. Между кольцом и кольцевой канавкой поршня, а так же между кольцом и стенкой гильзы существуют зазоры. Кроме того для обеспечения возможности сборки у кольца есть разъём, называемый замком. Через эти зазоры происходят утечки рабочего тела из камеры сгорания. Ниже компрессионных располагаются маслосъёмные кольца (одно, или реже два), которые служат для снятия излишков масла со стенки гильзы.

Утечки через кольца, особенно через изношенные, могут оказывать сильное влияние на параметры газа в цилиндре, изменяя индикаторную диаграмму и показатели двигателя. Потеря массы рабочего тела ведёт к уменьшению давления и, как следствие, работы цикла. Так же уменьшается и температура в цилиндре, ухудшая тем самым условия сгорания топливо-воздушной смеси, что приводит к ухудшению эффективных и экологических показателей двигателя. Более того изменение давления и температуры газов в объёмах между кольцами, вызванное утечками через них, сказывается на теплонапряженном состоянии деталей, так как изменяются условия теплообмена между поршнем и гильзой цилиндра.

На практике для оценки состояния цилиндро-поршневой группы используется замер компрессии — максимального давления цикла достигаемого в цилиндре двигателя без процесса сгорания. Для измерения этого давления используют прибор, называемый компрессометром (рисунок 1), который устанавливается вместо свечи в двигателе с воспламенением искрой или форсунки в двигателе с воспламенением от сжатия. При измерении компрессии коленчатый вал приводится в движение от стартёра или же остальными цилиндрами двигателя. Замер компрессии проводится на двигателе, выведенном на рабочий тепловой режим. В зависимости от технического состояния двигателя компрессия в цилиндре двигателя отличается. Обычно производитель устанавливает допустимые значения компрессии, которые указываются в руководстве по эксплуатации или ремонту.

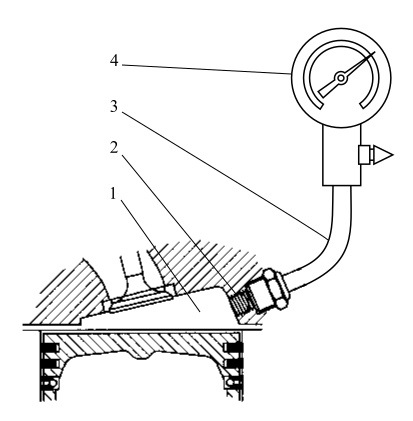
Рис. 1. Схема замера компрессии двигателя с искровым зажиганием: 1 — камера сгорания, 2 — резьбовое отверстие для установки свечи, 3 — присоединительный шланг, 4 — манометр

Геометрия, формируемая кольцами и кольцевыми канавками, не только сложна, но и непостоянна во времени, поскольку кольца при нормальной работе перекладываются с верхнего торца на нижний, проворачиваются вокруг оси поршня и скручиваются, поршень перекладывается в гильзе, а под действием температуры происходит деформация канавок и колец. Поэтому решение задачи расчёта утечек в полной постановке, особенно при расчете рабочего процесса двигателя, затруднено. В программах моделирования рабочего процесса зачастую вводится абстрактная величина μf_L — эффективная площадь проходного сечения поршневых колец, принимаемая постоянной.

Размеры колец и кольцевых канавок, зазоров в замке кольца подбираются в узких пределах в зависимости от диаметра цилиндра D двигателя, поэтому предположим, что величина μf_L так же зависит от D. Алгоритм создания аппроксимирующей зависимости для расчета μf_L(D) предполагает следующие этапы:

– определение μf_L для двигателей с разными D путем подбора эффективной площади проходного сечения колец при расчёте компрессорных ходов до совпадения экспериментального и расчетного значений максимального давления;

– аппроксимация полученного набора данных μf_L(D) с помощь полинома.

Метод решения.

Для решения использовано математическое моделирование компрессорного хода (работа без сгорания) в цилиндре. Применена термодинамическая модель, включающая цилиндр, пространства между кольцами и картер двигателя.

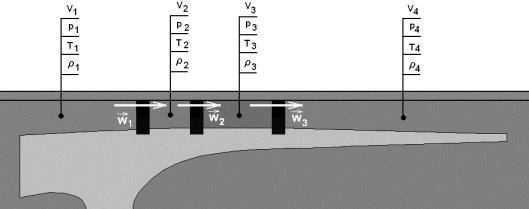
Рис. 2. Схема модели расчёта компрессорных ходов с учётом утечек через кольца для двигателя с тремя поршневыми кольцами [1]

Процессы в цилиндре и объемах между кольцами описаны первым законом термодинамики для открытой системы, законом сохранения массы и уравнением состояния идеального газа:

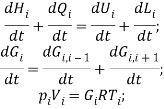
Распишем первый закон термодинамики:

где — энтальпия, поступившая в зону i, вследствие массообмена с предыдущей (i-1) и следующей (i+1) зонами, Дж; — теплота, подведённая вследствие теплообмена со стенкой, Дж; — внутренняя энергия газа, Дж; — работа, совершённая газом, Дж.

Для цилиндра под массообменом с предыдущей зоной понимается массообмен через выпускные (G_EX) и впускные (G_IN) клапана, соответственно изменение энтальпии для данного объема:

Поскольку объём пространства между кольцами принимается постоянным, работа в них не совершается:

Изменение энтальпии определяется как:

гдеC_p0 — изобарная теплоёмкость текущего газа, Дж/(кг К); T₀ — температура текущего газа, К; — массовый расход газа через клапана или зазоры колец, кг/с.

Расход газа через клапана и кольца:

где ρ₀ — плотность текущего газа, кг/м³; μf — текущая эффективная площадь проходного сечения, м²; w — скорость течения газа, м/с.

Скорость течения газа через клапана и сквозь кольца рассчитывается с использованием газовой динамики для задачи в стационарной постановке:

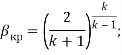
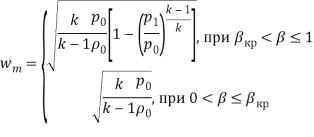
где p₀, ρ₀ — давление (Па) и плотность (кг/м³) в объёме, из которого происходит истечение; p₁ — давление в объёме, в который происходит истечение, Па; k — газовая постоянная газа, Дж/(кг К).

Причём при расчёте газообмена двух объёмов p₀ и p₁ выбираются так что p₀ > p₁, поэтому w_m лишь модуль скорости, направление потока учитывается сравнением давлений в расчётном объёме (i) и объёме, с которым происходит газообмен (i+1).

p_i > p_i+1:p₀ = p_i,p₁ = p_i+1, ρ₀ = ρ_i,w = -w_m;

p_i< p_i+1:p₀ = p_i+1,p₁ = p_i, ρ₀ = ρ_i+1,w = w_m.

Закон изменения эффективной площади проходного сечения клапанов принят за синусоидальный:

,

где φ_loc — «локальный» угол поворота коленчатого вала, с нулём в точке начала открытия клапана, °; φ_val — полная продолжительность открытия клапана, °; — максимальная эффективная площадь проходного сечения клапанов, м².

Эффективная площадь проходного сечения колец принята постоянной на всём протяжении цикла и одинаковой для всех колец, в том числе и для маслосъёмного.

Количество теплоты, подведённой в результате теплообмена, определяется по формуле Ньютона-Рихмана:

где α_w — средний коэффициент теплоотдачи от газа к стенке, Вт/(м² К); T_w — средняя температура стенки, К, принята постоянной; T — температура газа в цилиндре, К; F_w — площадь поверхности теплоотдачи, м².

В цилиндре коэффициент теплоотдачи определяется по эмпирической формуле Вошни [2]. В объёмах между кольцами коэффициент теплоотдачи рассчитывается по формуле для течения жидкости по трубе:

где — критерий Нуссельта; — число Рейнольдса; — число Прандтля; — число Прандтля, рассчитанное по температуре стенки; l — характерная длина, в данном случае — высота между кольцами, м; λ’ — коэффициент теплопроводности, Вт/(м К); — эквивалентный диаметр трубы, м.

Площадь теплообмена для цилиндра состоит из поверхностей днища поршня F_ДП, крышки цилиндра F_КЦ и текущей площади гильзы F_Г(φ) и определяется как:

В объемах между кольцами площадь рассчитывалась по формуле:

где h_кол — расстояние между кольцами, м.

Изменение внутренней энергии:

где C_v — изохорная теплоёмкость газа, Дж/(кг К); G — масса газа в цилиндре, кг.

В расчетах принималась зависимость теплоемкости газа от температуры, тогда изменение внутренней энергии, входящее в Первый закон термодинамики, запишем в следующем виде

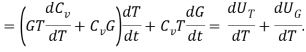
Для расчёта изохорной и изобарной теплоёмкости газов используется эмпирическое выражение в виде полинома шестой степени:

для воздуха коэффициенты имеют значения: x= (T-273,15)/1000;C₀= 718,506574;C₁= -0,604835; C₂= 234,693349;C₃= -236,414469;C₄= 115,188305;C₅= -28,667784;C₆= 2,906563.

А так же закон Майера:

C_p — C_v = R,

где R — газовая постоянная, для воздуха R = 287,0 Дж/(кг К).

Соответственно производная от изохорной теплоёмкости по температуре:

Элементарная работа, совершённая газом:

где p — давление газа, Па; V — текущий объём цилиндра, м³.

Закон изменения объёма цилиндра следует из кинематики преобразующего механизма, для центрального кривошипно-шатунного механизма (рисунок 3) перемещение поршня выражается как:

где S — полный ход поршня, м; λ — отношение радиуса кривошипа к длине шатуна.

Тогда объём цилиндра от угла поворота коленчатого вала:

— объем камеры сгорания в ВМТ, м³; ε — степень сжатия.

Производная от объёма цилиндра по углу поворота коленчатого вала в свою очередь имеет вид:

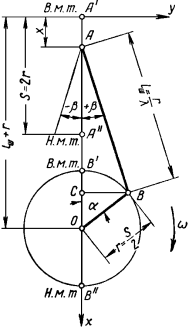
Рис. 3. Центральный кривошипно-шатунный механизм

Окончательно Первый закон термодинамики (для каждого контрольного объема) перепишем в виде:

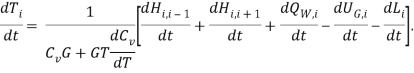
Последняя зона (картер) обладает гораздо большим объёмом, чем объёмы цилиндра или межколечных пространств. Так же на двигателях устанавливается сапун, для сброса избытка давления из картера, поэтому давление, температура и масса газа в этой зоне задаются постоянными.

Решение системы уравнений осуществляется численно — методом Рунге-Кутта [3]. Шаг расчёта задавался в углах поворота коленчатого вала и пересчитывался в шаг по времени в зависимости от частоты вращения коленчатого вала n. Величина шага выбирается так, чтобы быть достаточной при расчёте термодинамических параметров в объемах между кольцами: они много меньше объёма цилиндра и в то же время сильно отличаются от него по давлению, вследствие чего процессы перетекания весьма интенсивны и требуют повышенной точности расчёта.

Расчёт рабочего процесса повторяется несколько раз, до тех пор пока термодинамические параметры в цилиндре в начале и конце цикла не совпадут с точностью 0,1 %, после чего рабочий цикл считается установившимся. После установления рабочего цикла, программа изменяет значение эффективной площади проходного сечения колец и повторяет расчёт вновь до тех пор пока значение компрессии не совпадёт с требуемым.

Исследование ирезультаты.

Исследование проводилось по известным данным, приведённым заводами изготовителями [4, 5], для нескольких автомобильных и тепловозных двигателей, как дизельных, так и бензиновых.

Таблица 1

Исходные данные [4, 5]

Двигатель	ВАЗ 2101	ЗМЗ 406	ЯМЗ 238	Д49
D, мм	76	92	130	260
S, мм	66	86	140	260
ε	8,5	9,3	17,5	13,5
λ	0,25	0,27	0,26	0,22
n, мин-1	400	400	440	500
Угол открытия выпускных клапанов, град до НМТ	42	46	66	50
Угол закрытия выпускных клапанов, град за ВМТ	10	14	20	35
Угол открытия впускных клапанов, град до ВМТ	12	14	20	55
Угол закрытия впускных клапанов, град за НМТ	40	46	46	30
Диаметр выпускного клапана, мм	31,5	31,5	48	88
Диаметр впускного клапана, мм	37	37	61	96
Ход выпускного клапана, мм	8	8	12	24
Ход впускного клапана, мм	9	9	15	24
Наибольший диаметр гильзы, мм	76,01	92,036	130,02	260,5
Наименьший диаметр поршня, мм	75,94	91,988	129,8	260
Расстояние между поршневыми кольцами, мм	6	7	10	14
Количество колец	3	3	3	4
Компрессия при максимальном износе колец, бар	10	12	20	25
Компрессия при минимальном износе колец, бар	12	-	27	-

Таблица 2

Рассчитанные данные

Двигатель	ВАЗ 2101	ЗМЗ 406	ЯМЗ 238	Д49
Максимальное эффективное проходное сечение выпускных клапанов, мм2	385,7	771,5	895,7	6568,4
Максимальное эффективное проходное сечение впускных клапанов, мм2	532,2	1064,4	1446,5	6866,9
Межколечный объём, мм3	100,3	404,6	898,5	5717,7

Таблица 3

Результаты численного эксперимента

Двигатель	ВАЗ 2101	ЗМЗ 406	ЯМЗ 238	Д49
Эффективное проходное сечение колец при их максимальном износе, мм	10,9	13	38,2	66
Эффективное проходное сечение колец при их минимальном износе, мм	2,7	-	5,8	-

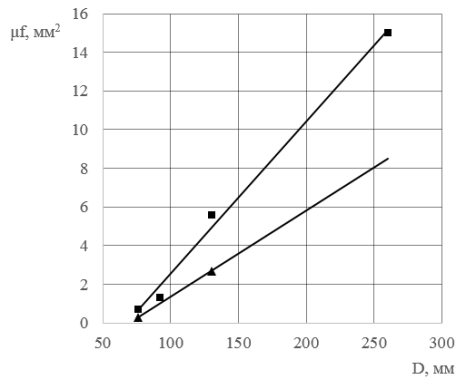
Рис. 4. Результаты численного эксперимента и полученные зависимости для износа поршневых колец

Эффективная площадь проходного сечения кольца (в мм²) при максимальном износе (i)

и минимальном износе

Если принять степень износа: 0 — для новых и 1 — для предельно изношенных, тогда в общем случае эффективная площадь проходного сечения колец в зависимости от диаметра цилиндра и степени их износа:

,

Заключение.

Разработана математическая модель, описывающая параметры состояния в цилиндре и объёмах между кольцами четырёхтактного двигателя внутреннего сгорания с учётом утечек через поршневые кольца, модель является термодинамической, а система уравнений решается численным методом Рунге-Кутта.

По известным данным подобраны значения эффективных площадей проходного сечения колец для двигателей с различными диаметрами цилиндра — таблица 3.

Получена эмпирическая формула эффективной площади проходного сечения поршневых колец от диаметра цилиндра для диапазона значений 76…260 мм и степени изношенности колец.

Литература:

1. Барченко Ф. Б., Иващенко Н. А. Расчёт давления между поршневыми кольцами двигателя внутреннего сгорания. // Вестник МГТУ им Н. Э. Баумана. — 2007. — Специальный выпуск — с. 80–85.
2. Теория поршневых и комбинированных двигателей / ред. А. С. Орлина, М. Г. Круглова — 3-е издание, переработанное и дополненное — Москва: Машиностроение, 1983.
3. Бахвалов Н. С., Жидков Н. П., Кобельков Н. С. Численные методы. — Москва: Бином, 2001.
4. Руководства по эксплуатации, техническому обслуживанию, ремонту. Двигатели КАМАЗ 740. — Набережные Челны: ОАО «КАМАЗ», 2002.
5. Ремонт двигателей ЯМЗ-236, 238, 240. Конструкция, принцип действия, диагностика неисправностей, ремонт. Практическое руководство. — «Сверчок Ъ», 2009.