Среди многочисленных схем газообмена легких двухтактных двигателей, наибольшее распространение получила кривошипно-камерная продувка. Двухтактные двигатели с данным типом продувки применяются на мотоциклах, снегоходах, бензопилах, газонокосилках и т. д. К его преимуществам можно отнести простоту конструкции, малую массу и низкую стоимость.
В двухтактных двигателях процессы впуска и выпуска совпадают по времени, поэтому вытеснение продуктов сгорания из цилиндра свежим зарядом сопровождается перемешиванием и приводит к частичной потере свежего заряда. Также на показатели двигателя оказывают существенное влияние нестационарные газодинамические процессы происходящие в кривошипной камере, во впускной и выпускной системах.
В настоящее время, создание новых образцов техники вплотную связано с использованием численного моделирования, которое позволяет сократить затраты и сроки при доводке конструкции. Моделирование рабочего процесса поршневого двигателя началось вместе с созданием данного типа двигателей. Основная сложность при моделировании рабочего процесса – это расчет сгорания. Однако для двухтактных двигателей явления, происходящие при продувке также очень важны и учет всех особенностей данного процесса является сложной задачей. Строго говоря, данные процессы должны моделироваться в трёхмерной постановке методами вычислительной газодинамики (CFD). Такой подход к моделированию требует больших вычислительных мощностей, и при этом расчёт может занимать десятки часов для одного режима работы двигателя. Традиционный [1–5] подход к моделированию рабочего процесса методами термодинамики позволяет кардинально сократить время счета с приемлемой для практики точностью.
В данной статье предлагается математическая модель рабочего процесса двигателя с кривошипно-камерной продувкой, основанная на законах термодинамики для цилиндра, кривошипной камеры, систем впуска и выпуска. При расчете рабочего процесса используется совместное решение квазистационарных систем дифференциальных уравнений для указанных 4 характерных объёмов. В качестве рабочего тела рассматривается смесь идеальных газов азота, кислорода, паров воды, диоксида углерода. Состояние рабочего тела в цилиндре, кривошипной камере, системе впуска и выпуска считается полностью равновесным. Далее подробно рассмотрена математическая модель цилиндра, а кривошипная камера, система впуска и выпуска рассчитывается по аналогии. Цилиндр представлен как открытая термодинамическая система, в которой рассматривается только одна зона, для которой рассчитывается давление и температура. При таких допущениях процессы, протекающие в цилиндре двигателя, описываются системой дифференциальных уравнений: первого закона термодинамики; сохранения массы; состояния:
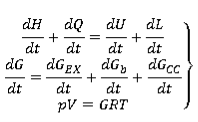 (1)
(1)
где H — энтальпия, Дж; Q — количество подведенного тепла, Дж; U — внутренняя энергия, Дж; G — масса газа в цилиндре, кг; dGEX/dt, dGCC/dt — расход газа через выпускные органы и продувочные окна соответственно, кг/с; dGb/dt — подвод массы в связи с топливоподачей, впрыском в цилиндр, кг/с.
Запишем уравнение первого закона термодинамики, системы уравнений (1) в развернутом виде.
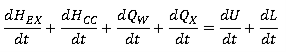 (2)
(2)
где HEX, HCC– энтальпия принесенная через выпускные органы и продувочные органы соответственно, Дж; QW, QX — количество тепла, подведенного в результате теплообмена и количество тепла, подведенного при сгорании топлива соответственно, Дж.
Распишем в явном виде все составляющие дифференциального уравнения (2). Энтальпия газа, прошедшего через выпускные органы цилиндра:
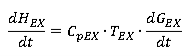 (3)
(3)
где: CpEX — изобарная теплоемкость газа, прошедшего через выпускные органы, Дж/(кг К); TEX — температура газа, прошедшего через выпускные органы, К.
Энтальпия газа, прошедшего через продувочные окна:
![]() (4)
(4)
где: CpCC — изобарная теплоемкость газа, прошедшего через продувочные окна, Дж/(кг К); TCC — температура газа, прошедшего через продувочные окна, К.
Истечение газа из одного характерного объёма в другой, происходит из-за перепада давлений, газодинамические явления не учитываются. При этом может наблюдаться два режима истечения: критический и докритический. Расход газа рассчитывается по формулам для энергоизолированного изоэнтропного процесса:
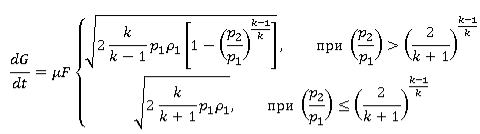 (5)
(5)
где ![]() — давление среды куда происходит истечение, Па;
— давление среды куда происходит истечение, Па;![]() — давление среды откуда происходит истечение, Па; k — показатель адиабаты;
— давление среды откуда происходит истечение, Па; k — показатель адиабаты; ![]() — удельный объём среды откуда происходит истечение, кг/м3;
— удельный объём среды откуда происходит истечение, кг/м3; ![]() — эффективное проходное сечение,м2.
— эффективное проходное сечение,м2.
Количество теплоты, подведенной в результате теплообмена:
![]() (6)
(6)
где: αW — коэффициент теплоотдачи, рассчитываемый по эмпирической формуле, Вт/(м2 К); T — температура газа в цилиндре, К; TW — эквивалентная температура стенок цилиндра, К; AW — площадь теплообмена, м2.
Количество теплоты, выделившейся при сгорании топлива:
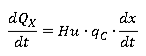 (7)
(7)
где: Hu — низшая теплота сгорания топлива, Дж/кг; qc — цикловая подача топлива, кг; dx/dt — скорость тепловыделения, 1/с.
Изменение внутренней энергии запишем в виде:
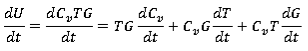 (8)
(8)
В связи с малым изменением теплоемкости газа за элементарный промежуток времени откинем член дифференциального уравнения (8), отвечающий за изменение теплоемкости, тогда изменение внутренней энергии можно записать в виде:
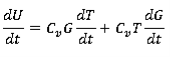 (9)
(9)
Элементарная работа, с учетом уравнения состояния идеального газа:
![]() (10)
(10)
где p — давление в цилиндре, Па; V — текущий объем цилиндра, м3; R — газовая постоянная, Дж/(кг·К).
Общий вид уравнения первого закона термодинамики в цилиндре (1) запишем следующим образом:
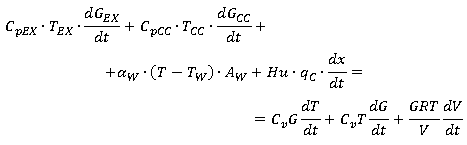 (11)
(11)
Перепишем дифференциальное уравнение (11) относительно температуры в цилиндре:
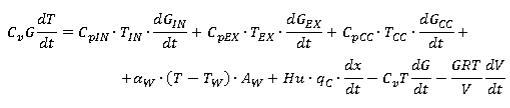 (12)
(12)
Рабочим телом является смесь газов, поэтому внутреннюю энергию, энтальпию, теплоемкость и газовую постоянную необходимо определять для смеси газов [6]. Причем теплоемкость каждого компонента смеси газов зависит от температуры. При расчете рабочего процесса данные по свойствам газов были взяты из справочной литературы [7].
Уравнение сохранения массы при непосредственном впрыскивании запишем в виде:
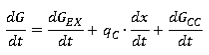 (13)
(13)
Такая запись моделирует подвод массы топлива в предположении мгновенного сгорания топлива, впрыскиваемого в цилиндр, при том, что скорость тепловыделения dx/dt задается формулой Вибе. Расчет массообмена через продувочные(dGCC/dt) и выпускные (dGEX/dt) органы ведется по формуле (5).
На рис. 1 а показана конструкция одноцилиндрового двухтактного двигателя с кривошипно-камерной продувкой, а на рис.1 б изображена его расчетная схема. На рис. 1 б стрелками указаны выбранные положительные направления массообмена. На основании предложенной математической модели была создана программа для расчета, общий алгоритм работы, которой приведен на рис. 2.
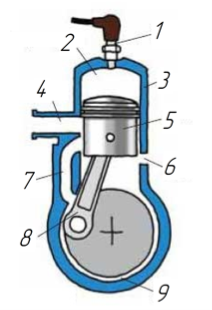
Рис. 1 а. Конструкция двигателя и его расчетная схема (конструкция двухтактного двигателя с кривошипно-камерной продувкой): 1 — свеча зажигания, 2 — камера сгорания, 3 — цилиндр, 4 — выпускной канал, 5 — поршень, 6 — впускное окно в кривошипную камеру, 7 — продувочный канал, 8 — шатун, 9 — кривошипная камера
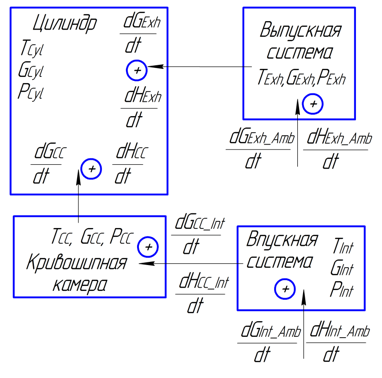
Рис. 1 б. Расчетная схема двигателя: GExh, GСyl, GСС, GInt — масса газа в системе выпуска, в цилиндре, в кривошипной камере, в системе впуска, соответственно, кг; TEX, TСyl, TСС, TInt — температура газа в системе выпуска, в цилиндре, в кривошипной камере, в системе впуска, соответственно, К; PEX, PСyl, PСС, PInt — давление газа в системе выпуска, в цилиндре, в кривошипной камере, в системе впуска, соответственно, Па; dGExh_Amb/dt, dGCC_Int/dt, dGInt_Amb/dt — массообмен системы выпуска с окружающей средой, кривошипной камеры с системой впуска, системы впуска с окружающей средой, соответственно, кг/с; dHExh_Amb/dt, dHCC_Int/dt, dHInt_Amb/dt — скорость изменения энтальпии при взаимодействии системы выпуска и окружающей среды, кривошипной камеры и системы впуска, системы впуска и окружающей среды, соответственно, Дж/с
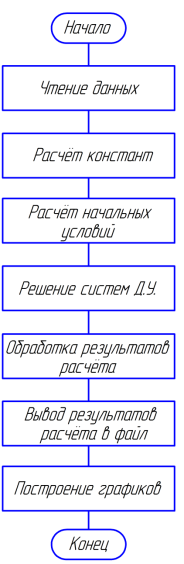
Рис. 2. Общий алгоритм программы
Для решения дифференциальных уравнений численными методами разработано много методов [8]. Система дифференциальных уравнений, включающих (12) и (13) решается численным методом Рунге-Кутта 4-ого порядка точности. На рис. 3 приведена блок-схема алгоритма расчета рабочего процесса двухтактного двигателя с кривошипно-камерной продувкой.
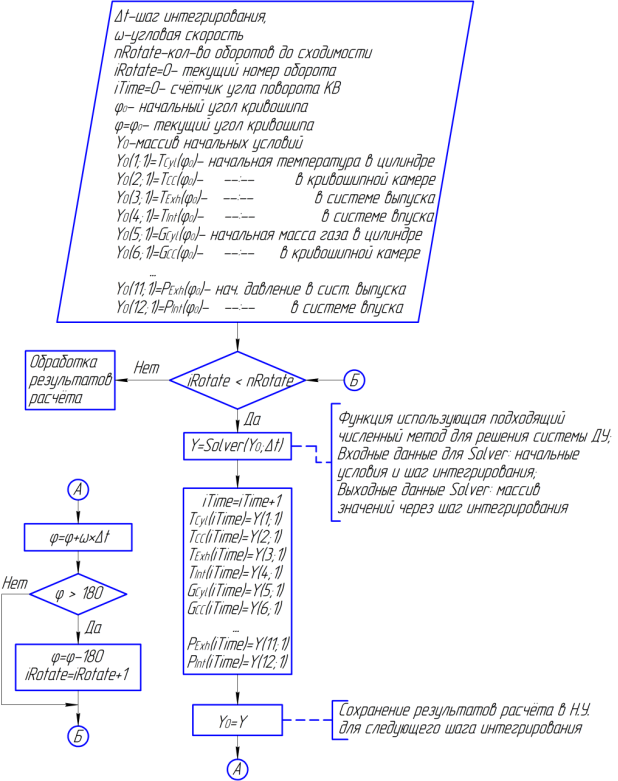
Рис. 3. Блок-схема алгоритма решения систем дифференциальных уравнений
После полного оборота коленчатого вала, значения температур, давлений, концентраций газов во всех объёмах используются как начальные условия для следующего рабочего цикла. Итерации продолжаются до тех пор, пока значения давления, температуры и состава газов в начальной точке расчёта не будут отличаться на величину погрешности: давление 1кПа; температура 3 К; состав газов 1 %. Опытным путем было установлено, что для сходимости необходимо 30–40 оборотов коленчатого вала, рис. 4.
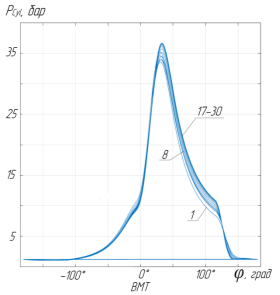
Рис. 4 а. Расчет рабочего процесса до сходимости: давление в цилиндре
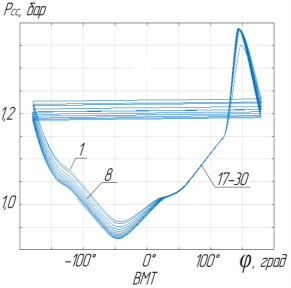
Рис. 4 б. Расчет рабочего процесса до сходимости: давление в кривошипной камере
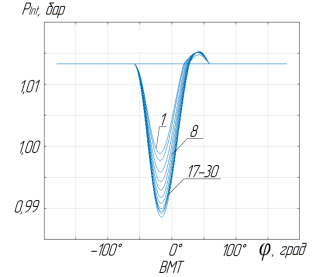
Рис. 4 в. Расчет рабочего процесса до сходимости: давление в системе впуска
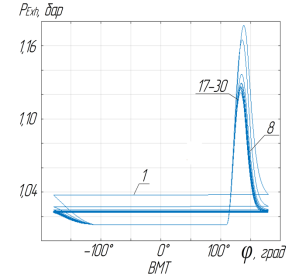
Рис. 4 г. Расчет рабочего процесса до сходимости: давление в системе выпуска; 1,8, 17–30 — номера итераций
Одной из задач данной работы было создание и отладка алгоритма расчёта рабочего процесса одноцилиндрового двигателя, которую следует считать выполненной. Используемая в настоящее время математическая модель с большими объемами на впуске и выпуске применима к двигателям мотопил, газонокосилок и прочей бытовой техники. Однако расчет высокооборотных двигателей данного типа с такими моделями впуска и выпуска будет не корректен, так как зачастую на этих двигателях устанавливают специальные настроенные резонансные трубы улучшающие очистку и наполнение цилиндра. В дальнейшем математическая модель будет усовершенствована применением одномерной газовой динамики для расчета систем впуска и выпуска, а также усложнением модели продувки цилиндра.
Литература:
- Жуков В. П., Павличенко А. М. Исследование характеристик тепловыделения ДВС по нагрузочной характеристике с помощью методов нелинейного программирования // Тр. Николаевского политехнического института. Николаев, 1976, Вып. 112. С. 50–56.
- Петрухин Н. В. Рабочий процесс и тепловая напряженность цилиндро-поршневой группы двигателей с уменьшенным теплоотводом от рабочего тела: Дисс. канд. техн. наук. Москва, 1988, 188 с.
- Процессы в перспективных дизелях / А. Ф. Шеховцов [и др.]; Под ред. А. Ф. Шеховцова. Харьков: Изд-во «Основа» при Харьк. Ун-те, 1992. — 352 с.
- Кулешов А. С. Расчетно-экспериментальный выбор параметров рабочего процесса 4-х тактного среднеоборотного комбинированного ДВС: Дисс. канд. техн. наук. М.: МВТУ, 1986. 124 с.
- Kuleshov A. S. Multi-Zone DI Diesel Spray Combustion Model for Thermodynamic Simulation of Engine with PCCI and High EGR Level // SAE Tech. Pap. Ser. 2009. № 2009–01–1956. P. 1–21.
- Теплотехника / А. М. Архаров, А. Г. Кузнецов, В. И. Шатров и др. Под ред. А. М. Архарова, В. Н. Афанасьева. Учебник для ВУЗов. Второе издание. М.: Изд-во МГТУ им. Н. Э. Баумана, 2004. 712 с.
- Варгафтик. Справочник по теплофизическим свойствам. М.: «Наука», 1972. 721 с.
- Хайрер Э., Нёрсетт С., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Нежесткие задачи. М.: Мир. 1990 г. 512 с.







