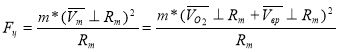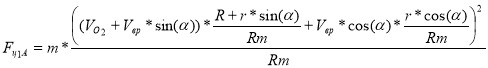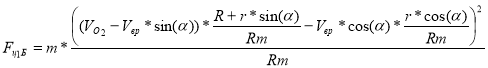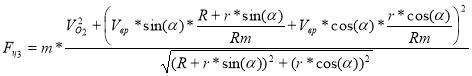Современная оценка влияния центростремительных сил на окружающий мир и технику. Разработка эффекта Марго
Автор: Филенко Алексей Владимирович
Рубрика: Общие вопросы технических наук
Опубликовано в Техника. Технологии. Инженерия №2 (16) май 2020 г.
Дата публикации: 14.03.2020
Статья просмотрена: 1065 раз
Библиографическое описание:
Филенко, А. В. Современная оценка влияния центростремительных сил на окружающий мир и технику. Разработка эффекта Марго / А. В. Филенко. — Текст : непосредственный // Техника. Технологии. Инженерия. — 2020. — № 2 (16). — С. 1-11. — URL: https://moluch.ru/th/8/archive/165/4984/ (дата обращения: 20.04.2024).
Исследование направлено на изучение особенностей изменения величины центростремительной силы, которая прикладывается к материальной точке относительно центра гравитации. Полученный эффект получил название эффекта Марго. Автором рассматриваются сферы применения данного эффекта и области, где влияние может быть наиболее сильным. Предложены направления для применения эффекта Марго в ходе реализации расчетов на производственных предприятиях (эксплуатация быстроходных и больших по диаметру турбин, а также ускорителей частиц). Кроме того, показано воздействие эффекта Марго на величину приливов, движение планет и спутников.
Ключевые слова: эффект Марго, центростремительная сила, центр, движение, сила, плоскость, движение материальных объектов, вращение планет.
Цель. Обосновать необходимость принятия во внимание эффекта Марго с целью повышения эффективности деятельности производственных предприятий в ряде отраслей хозяйствования, а также при анализе природных явлений.
Задачи. Для реализации поставленной цели рассматривается понятие силы в рамках классической механики Галилея-Ньютона. Разрабатываются формулы движения материальных точек, вращающихся вокруг тела, при движении этого тела вокруг центра гравитации. Приводятся доказательства эффективности применения эффекта Марго при проведении расчетов на производственных предприятиях.
Методология. Висследовании использовалась методология системного подхода к изучению физических явлений и процессов, а также метод системного анализа.
Результаты. Было установлено, что у материальной точки, вращающейся вокруг тела, при учёте того что это тело вращается на орбите вокруг центра в его гравитационном поле, при изменении углов положения плоскости вращения материальной точки вокруг тела (изменение углов Эйлера) относительно плоскости вращения тела вокруг центра гравитации, будет изменяться величина центростремительной силы, прикладываемая к материальной точке относительно центра гравитации. Данный эффект получил название эффекта Марго. Представлены расчеты по эффективности применения данной методики в ряде отраслей промышленности (эксплуатация турбин, ускорители частиц), а также при анализе физических явлений (приливы, движение спутников и планет).
Обратимся к основному различию общего понятия «теоретическая механика», вытекающему из классической механики Галилея-Ньютона (наука об общих законах механического движения и взаимодействия материальных тел) и небесной механики, которая позволяет вычислять движения небесных тел и явлений, основанных на законах Ньютона.
Как мы знаем, для учета меры механического взаимодействия между телами в классической механике, основание которой положили Галилео Галилей и Исаак Ньютон, вводится понятие о силе. Для определённого тела сила является внешним фактором, изменяющим его движение. Характер движения зависит как от силы, так и от степени инертности тела.
Чем больше инертность тела, тем медленнее изменяется его движение под действием данной силы, и наоборот. Мерой инертности тела является его масса. Таким образом, понятиями, лежащими в основе классической механики, являются движущаяся материя (материальные тела), пространство и время как формы существования движущейся материй, масса как мера инертности материальных тел и сила как мера механического взаимодействия между телами.
В классической механике Галилея-Ньютона пространство считается трехмерным евклидовым. Его свойства не зависят от движущихся в нем материальных объектов. Положение точки в таком пространстве относительно какой-либо системы отсчета определяется тремя независимыми параметрами, или координатами точки.
Время в классической механике универсально. Оно не связано с пространством и движением материальных объектов. Во всех системах отсчета, движущихся друг относительно друга, оно протекает одинаково. Массы материальных объектов не зависят от скорости их движения. Несмотря на это, классическая механика Галилея-Ньютона продолжает сохранять свою огромную ценность как мощное орудие научного исследования различных вопросов естествознания и техники, а ее законы дают при этом вполне достаточную для практики точность.
В динамике изучается механическое движение материальных объектов с учетом их взаимодействия с окружающими материальными телами и средой, т. е. с учетом сил, действующих на эти объекты. В динамике в отличие от статики, как активные силы, так и реакции связей — в основном переменные величины. Активные (заданные) силы могут зависеть от времени, положения и скоростей точек в системе, а реакции связей еще и от их ускорений.
Ссылаясь на очерки Белецкого, мы видим, что дифференциальные уравнения, описывающие реальные физические объекты, [5, C.17] не интегрируются. Почти все задачи механики, к сожалению, описываются неинтегрируемыми уравнениями. Лишь очень немногие задачи относятся к интегрируемым, как, например, задача о движении двух материальных точек под действием силы взаимного тяготения.
Соответственно, если использовать дифференциальные уравнения (далее ДУ) из теории небесной механики применимо к материальным точкам, то проблем не возникает. Но как только мы вспоминаем, что небесные тела — это не материальные точки, то понимаем, что эти ДУ имеют определенную погрешность. И описываемый эффект создается именно этими небольшими отброшенными для удобства вычислений ДУ сил. Используемые сейчас ДУ из теории небесной механики при постановке вопроса о движении планет имеют определенную погрешность и, более того, законы Кеплера только описывают движения планет, но в них не видна причина, почему это движение приходит к нынешнему виду.
Соответственно, во всей теории небесной механики присутствует описание — как движутся планеты (законы Кеплера), но не видны причины, вызывающие это движения. Через ДУ эффект Марго никаким образом не проявляется, так как для возможности вычислений ДУ отбрасывается та небольшая составляющая силы действующей на тело которая проявляется в виде эффекта Марго. ДУ совершенно справедливы только для движущихся материальных точек.
Рассматривая законы Кеплера, описывающие движения планет, мы видим доказательную базу того, что движения происходит по эллипсоиду, но не видим первоочередного — причину, благодаря которой это движение происходит. Все расчёты, для реальных объектов, произведённые при помощи ДУ, естественным образом являются приблизительными (см. выше).
Соответственно, для увеличения точности расчётов, мы можем позволить себе вернуться к первоначальным уравнениям Ньютона. Это более затратный в вычислительном понимании этого слова процесс, но более точный, так как из этих уравнений ничего выбрасывать не надо. В данных уравнениях погрешность будет на уровне погрешностей самого компьютера.
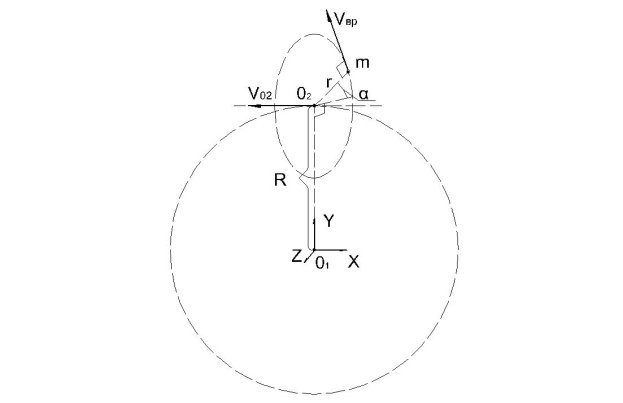
Рассмотрим систему, где центр координат это О1, в центре О1 находится центр гравитации, вокруг центра О1 по орбите движется центр О2, на расстоянии R в плоскости X-O1-Y со скоростью Vо2 — орбитальная скорость центра О2. Вокруг центра О2 вращается материальная точка со следующими параметрами: m — масса материальной точки, Vвр — скорость вращения материальной точки вокруг точки О2, ![]() - угловая скорость вращения материальной точки вокруг точки О2, r — расстояние от центра О2 до материальной точки, Vm — скорость движения материальной точки относительно точки О1.
- угловая скорость вращения материальной точки вокруг точки О2, r — расстояние от центра О2 до материальной точки, Vm — скорость движения материальной точки относительно точки О1.
Основная центростремительная сила возникает при движении материальной точки вокруг О1, фактически движение О2 вокруг О1, и рассчитывается по формуле:
|
|
[1] |
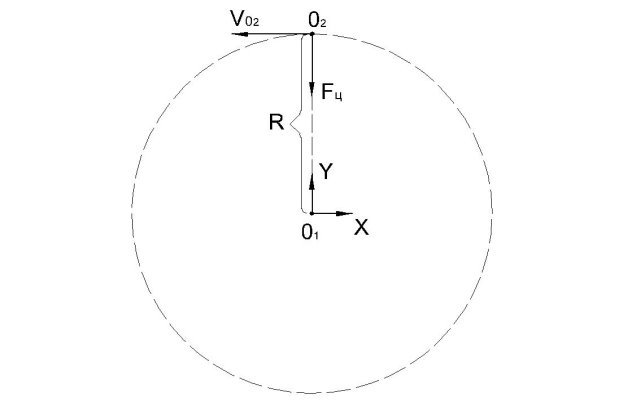
Рис. 1
но т. к. материальная точка дополнительно имеет движение вокруг точки О2 то сила будет вычисляться по формуле:
|
|
[2] |
выражение [1] отличается от выражение и соответственно силы неподвижной, относительно О2, и вращающейся материальной точки, вокруг О2, не одинаковы. Произведём дальнейшее преобразование выражения [2] из векторной формы в скалярную форму, необходимо найти формулу для ![]() перпендикулярного Rm и
перпендикулярного Rm и ![]() перпендикулярного Rm.
перпендикулярного Rm.
Для изучения зависимости Fц от изменения пространственного положения плоскости вращения материальной точки, относительно плоскости вращения О2 вокруг О1. Рассмотрим движение материальной точки в трёх плоскостях.
Движение в первой плоскости.
Плоскость движения материальной точки находится в плоскости движения центра О2 т. е. принадлежит плоскости X-O1-Y.
Вариант А.
Направление вращения материальной точки вокруг точки О2 совпадает с направлением вращения О2 вокруг О1 (см. Рисунок 2).
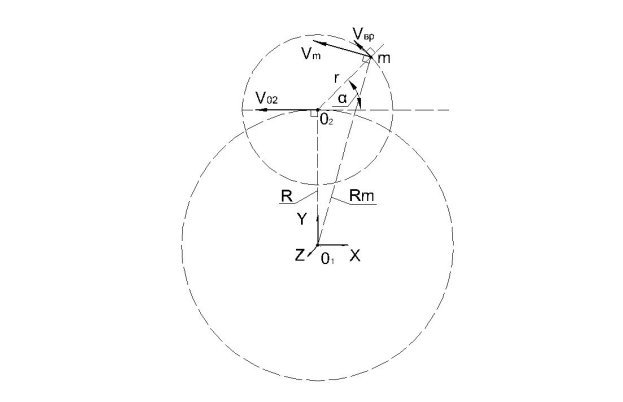
Рис. 2
Запишем Rm в виде:
|
|
[3] |
Тогда возникающую центростремительную силу, приложенную к материальной точке относительно центра О1, используя выражение [3], можно записать следующим образом:
|
|
[4] |
При r<
[5]
Анализ данного выражения показывает, что при
[6]
Выражение [6] равно центростремительной силе при движении материальной точке только вокруг центра О1 по радиусу R. Т. е. в точках
Также можно записать следующую зависимость величины центростремительной силы от угла
[7]
Выражение [7] показывает, что движение в плоскости 1 вариант А устойчивое, возникающие дополнительные силы в случае незначительного отклонения от плоскости XO1Y будут возвращать движение материальной точки в плоскость XO1Y.
При этом вращении дополнительные силы приводят к возникновению орбиты в виде эллипса.
Вариант Б.
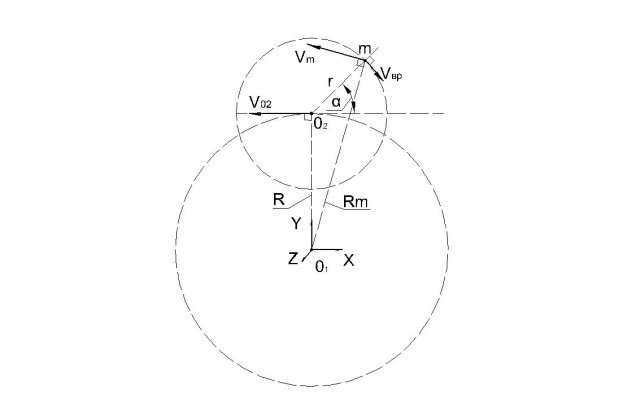
Направление вращения материальной точки вокруг точки О2 противоположно направлению вращения О2 вокруг О1 (см. Рисунок 3).
Рис. 3
![]()
![]() и
и ![]() выражение [5] примет вид:
выражение [5] примет вид:
![]()
![]() и
и ![]() не возникает дополнительных возмущений.
не возникает дополнительных возмущений.
![]() ,
,
![]()
|
|
[8] |
При r
[9]
Анализ выражения [9] показывает, что при
[10]
Т. е. выражение [10] равно центростремительной силе при движении материальной точки только вокруг центра О1 по радиусу R. Т. е. в точках
Так же можно записать следующую зависимость величины центростремительной силы от угла
[11]
Выражение [11] показывает, что движение в плоскости 1 вариант Б — НЕ устойчивое, в случае незначительного отклонения от плоскости X-O1-Y дополнительные силы будут усиливать это отклонение.
Движение во второй плоскости.
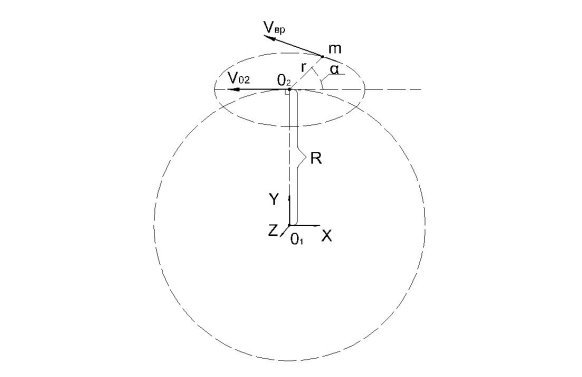
Плоскость движения материальной точки находится в плоскости X-O2-Z (см. Рисунок 4).
Рис. 4
Тогда возникающую центростремительную силу, приложенную к материальной точке относительно центра О1, в скалярном виде можно записать следующим образом:
[12]
[13]
Анализ данного выражения показывает, что при
[14]
Т. е. выражение [14] больше центростремительной силы при движении материальной точки только вокруг центра О1 по радиусу R. Т. е. в точках
Так же можно записать следующую зависимость величины центростремительной силы от угла
[15]
Выражение [15] показывает, что движение в плоскости 2 — НЕ устойчивое, возникающие дополнительные силы стремятся движение во второй плоскости привести к движению в первой плоскости вариант А.
Проведенные числовые расчёты показали, что среднее значение дополнительно создаваемой силы, из всех возможных случаев, во второй плоскости максимально.
Движение в третьей плоскости.
Плоскость движения материальной точки находится в плоскости Y-O2-Z (см. Рисунок 5).
Рис.5
Запишем Rm в виде:
[16]
![]()
![]() и
и ![]() примет вид:
примет вид:
![]()
![]() и
и ![]() не возникает дополнительных возмущений.
не возникает дополнительных возмущений.
![]() ,
,
![]()
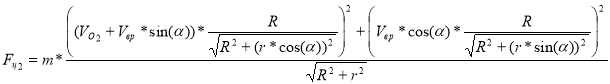
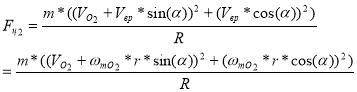
![]() и
и ![]() выражение [13] примет вид:
выражение [13] примет вид:
![]()
![]() и
и ![]() возникают дополнительные возмущения.
возникают дополнительные возмущения.
![]() ,
,
![]()
![]()
|
|
[17] |
При r
[18]
Численные расчёты выражения [18] показали, что при вращении в третьей плоскости, возникающие суммарные приливные силы минимальные по сравнению с вращением в двух остальных плоскостях.
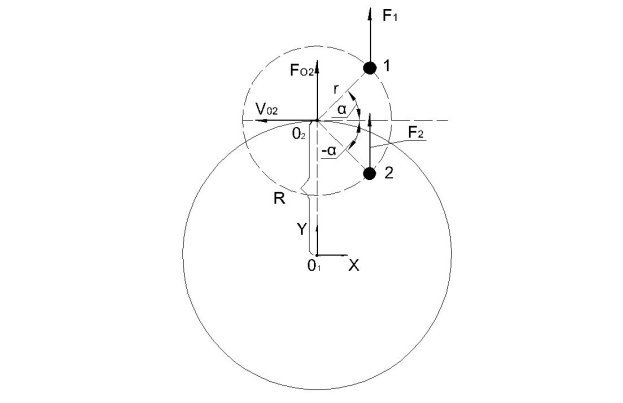
Рис.6
Рассмотрим точки О2,1 и 2, возникающие силы в этих точках FO2, F1 и F2 (см. Рисунок 6). Сила FO2 рассчитывается по формуле [1], силы F1 и F2 будем рассчитывать по формулам [4], [8], [12] и [17]. Силы F1 и F2 рассчитываются при симметричных углах
[19]
Рассмотрим вариант при котором R>>r для формулы [17] после преобразования и отбросив маленькие величины получим неравенство [20]:
[20]
Произведём такое же преобразование для формул [4] и [8] получим неравенство [21]:
[21]
По формулам [20] и [21] видно, что сила, создаваемая в третьей плоскости меньше чем при вращении в первой плоскости. Т. к. силы F1 и F2 рассчитанные по формуле [12] будут больше чем рассчитанные по формулам [4] и [8], тогда можно говорить, что сила создаваемая при дополнительном вращении материальной точки в любой плоскости вокруг О2 и двигающаяся вокруг центра О1, всегда увеличивает центростремительную силу по сравнению с материальной точкой которая только движется вокруг центра О1.
Основной вывод — у материальной точки, вращающегося на орбите вокруг центра О1 в его гравитационном поле и вращающейся вокруг центра О2, при изменении плоскости вращения вокруг центра О2 относительно плоскости вращения вокруг центра О1 будет меняться величина центростремительной силы, прикладываемой к материальной точке относительно центра О1, название эффекта — эффект Марго.
Как следствие, если взять объект, вращающийся на орбите вокруг центра О1, в его гравитационном поле, и вращающегося вокруг собственной оси, и представим этот объект как набор материальных точек, которые вращаются по орбитам с центром, находящимся на оси вращения объекта, то есть О2 принадлежит оси вращения этого объекта. Тогда к каждой отдельной материальной точке этого объекта и соответственно ко всему объекту применим эффект Марго.
![]()
![]() на интервале от 0 до
на интервале от 0 до ![]() . Тогда соотношение [19] будет показывать что даёт вращение материальной точки вокруг О2.
. Тогда соотношение [19] будет показывать что даёт вращение материальной точки вокруг О2.
![]() ??
?? ![]()
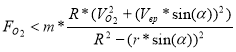
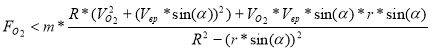
Фактически эффект Марго — это смесь центростремительной силы, силы Кориолиса и неравномерного гравитационного поля. Реальность эффекта Марго и, в частности, вывода о том, что самое устойчивое движение — вариант 1А (Рисунок 2), подтверждается устройством видимого космоса, а именно:
– вращение планет вокруг своей оси против часовой стрелки, если смотреть на солнечную систему таким образом, чтобы планеты двигались против часовой стрелки при условии, что вращение вокруг своей оси достаточно для проявления эффекта Марго.
– движение планет в солнечных системах и спутников вокруг планет — против часовой стрелки, если смотреть на галактику таким образом, чтобы звёзды двигались против часовой стрелки.
– движение планет в солнечных системах с небольшим отклонением от общей эклиптики.
– движение звёзд в галактиках таким образом, что создаётся плоская форма галактики.
Можно предположить, исходя из форм галактик, что их центры вращаются вокруг центра вселенной, что приводит к формированию плоского вида галактик. Расположение центра вселенной можно найти пересечением усреднённых плоскостей эклиптик трёх галактик, при условии, что эти три плоскости не принадлежат попарно одной плоскости.
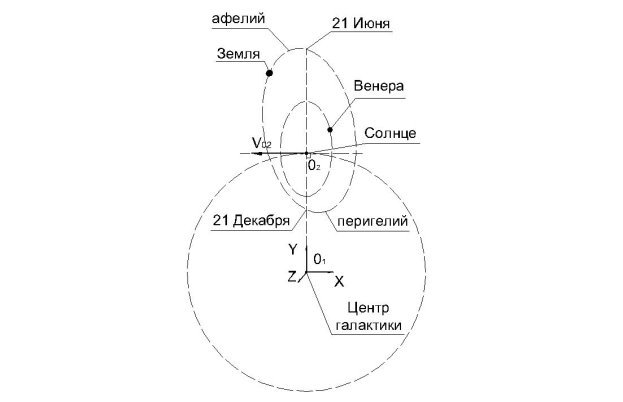
Рис. 7
Предположительное устройство галактики, представлено на схеме (Рис. 7). На данной схеме поясняется расположение центров вращения для применения формул эффекта Марго. По причине вращения планет в первой плоскости варианта А эффекта Марго, вокруг Солнца и движения Солнца вокруг центра галактики (точка О1), возникают силы, создающие у планет нашей Солнечной системы траекторий в виде эллипса. Самая наглядная планета — это Венера, поскольку она практически не вращается вокруг своей оси, то её эллиптическая орбита вызвана приливными силами, создающимися в соответствии с движением в первой плоскости варианта А, эффекта Марго.
Дополнительно у планеты Земля присутствует вращение вокруг собственной оси с углом отклонения оси вращения Земли от перпендикуляра к плоскости её орбиты. И соответственно в течении года будет меняться приливная сила, воздействующая на планету Земля, в соответствии с эффектом Марго, в результате чего на планету Земля будет воздействовать переменные приливные силы от двух гравитационных центров О1 (в одном случае это центр галактики, а во втором Солнце), вследствие чего эксцентриситет орбиты (те вытянутость эллиптической орбиты) планеты Земля больше чем у планета Венера.
И реальность эффекта Марго подтверждается вращением оси эллипса орбиты Земли вокруг центра нашей галактики, О1.
Области применения эффекта Марго:
– Приливы
При создании достаточно точной модели, описывающую форму и размеры Земли, и используя точные параметры скоростей (скорость вращения Земли, скорость движения Земли вокруг гравитационных центров) и расстояний до самых сильных гравитационных центров (Луна, Солнце), можно очень точно рассчитать силы, создающие приливы на Земле.
– Эксплуатация турбин
На графиках (Рисунок 8), построены изменение веса вдоль лопатки, вращающейся турбины на 60 параллели. По оси У откладывается разница между весом в верхней мертвой точкой и нижней мертвой точкой в ньютонах*10–6, для участка лопатки размером 1мм*1мм*360°/2000. Радиус лопатки откладывается по оси Х в метрах. Три верхние кривые построены для турбины вращающейся в первой плоскости вариант А эффекта Марго. Самая нижняя кривая (совпадающая с осью Х) это для турбины с частотой вращения 12000 об/мин в третьей плоскости эффекта Марго.
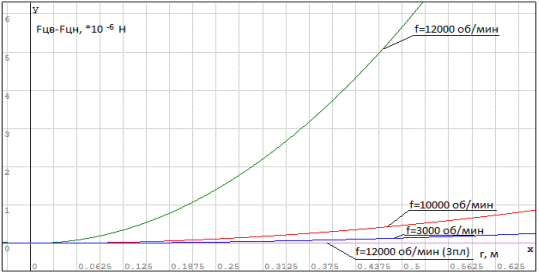
Рис. 8
Рассмотрим участок лопатки с массой 3,702*10–6 кг, вращающейся на радиусе 0,3м, при частоте 12000 об/мин, тогда изменение веса для этого участка будет ≈2,03*10–6Н. Вроде немного, но изменение происходит 12000 раз в минуту и если перевести в ваты, то участок лопатки будет периодически деформироваться с мощностью 0.000494446878Вт или 27,6Вт/час и это только для небольшой части турбины, с массой 3,702*10–6 кг, вращающейся на радиусе 0,3м. Не удачное позиционирование турбины на местности будет приводить к потерям мощности и разрушениям турбины.
Для снижения воздействия приливных сил, воздействующих на турбину, необходимо позиционировать турбину таким образом, чтобы ось турбины была параллельна земным меридианам широты, тогда лопатки будут вращаться в третьей плоскости эффекта Марго.
– Расчет траектории искусственных спутников
Возможно, повысить точность расчётов траектории искусственных спутников Земли, хотя на это могут потребоваться большие вычислительные мощности по сравнению с ДУ. Дополнительно можно будет понять, почему спутники «произвольно» меняют свою орбиту, на самом деле, на них воздействуют силы эффекта Марго, которые по умолчанию «сокращены» из ДУ. Самое простое замечание — самая стабильная орбита для ИСЗ та, которая находится в эклиптике Земли, хотя с течением времени она будет принимать эллиптическую форму.
– Ускоритель частиц
Гипотетически увеличивает точность работы ускорителя частиц.
Если расчёты движения частиц в ускорителях частиц производятся по ДУ то, как нетрудно понять из вышесказанного в этих расчётах, будет присутствовать определённая погрешность, избежать которую возможно при применении формул эффекта Марго.
– Мощные лазеры
При расположении световода в неравномерном гравитационном поле в плоскости 2 эффекта Марго, возможно создать подъемную силу. Движущиеся фотоны в гравитационном поле планеты будут создавать центростремительную силу. Аналогично возможно создать устройство для корректировки орбиты ИСЗ, т. к. оно будет работать только в сильном гравитационном поле планеты — на низких орбитах, при вращении маховиков во второй плоскости эффекта Марго, возможно создать небольшую центростремительную силу, направленную от центра гравитации (центра планеты).
Выводы
- У тела, вращающегося на орбите вокруг центра О1 в его гравитационном поле и вращающегося вокруг центра О2, при изменении плоскости вращения вокруг центра О2 относительно плоскости вращения вокруг центра будет меняться величина центростремительной силы, прикладываемой к материальной точке относительно центра О1, название эффекта — эффект Марго.
- Для движущегося по орбите объекта (планеты) вокруг гравитационного центра и вращающегося вокруг собственной оси при изменении положения собственной оси вращения относительно плоскости вращения объекта вокруг гравитационного центра О1, будет меняться центростремительная сила относительно центра О1 как на отдельные части объекта, так и суммарная центростремительная сила, действующая на весь объект в целом, т. е. эффект Марго применим к объектам и планетам.
- Области, где приливные силы и эффект Марго особенно заметны:
– Расчёт приливных сил.
– Движение планет и спутников, в т. ч. искусственных спутников.
– Быстроходные и большие по диаметру турбины.
– Ускорители частиц.
– С учётом формул эффекта Марго найти правильное значение коэффициента G- гравитационной постоянной.
Литература:
- Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — 592 с.
- Савельев И. В. Курс общей физики. Т. 1. Механика. Молекулярная физика. — М.: Наука, 1987. — 520 с.
- Механика в техническом университете // Под ред. К. С. Колесников — М. Издательство МГТУ имени Н. Э. Баумана, 2005. — 544 с.
- Дубошин Г. Н. Небесная механика основные задачи и методы: 2-е издание переработанное и дополненное. — М.: Наука, 1968. — 456 с.
- Белецкий В. В. Очерки о движении космических тел. № 40. Изд. стереотип. URSS. 2017. — 432 с.
Ключевые слова
сила, центр, плоскость, движение, эффект Марго, центростремительная сила, движение материальных объектов, вращение планетПохожие статьи
От кинематических законов Галилея и Кеплера к динамическим...
Для поддержания равномерного прямолинейного движения сила не нужна (Галилей). Для осуществления остальных видов движений (по отношению к ним суждения Аристотеля справедливы) необходима сила, которая определяется формулой (второй закон Ньютона)
Успехи небесной механики | Статья в журнале «Юный ученый»
Небесная механика (англ. celestial mechanics) — раздел астрономии, применяющий законы механики для изучения движения небесных тел. Небесная механика занимается вычислением положения Луны и планет, места и времени затмений...
Моделирование движения космических тел для исследования...
Моделирование движения произвольного количества тел в космосе — Земли, Луны и
Для этого в центр масс поместим условную звезду, с массой равной сумме масс Сириуса A и
Теперь точно так же запустим планеты, оставив в центре планетарной две звезды: Сириус A и...
К механизму взаимодействия гравитации и массы
Успехи небесной механики | «Молодой. Разработка общих вопросов движения небесных тел в гравитационном поле.
Простейшую модель центрального поля шара построил Ньютон.
Отдельно изучается сила тяжести как сила, действующая со стороны Земли на любое тело...
Использование библиотеки SFML для визуализации результатов...
Небесная механика также включает в себя законы Кеплера (первый закон: орбита планеты имеют форму эллипса, в одном из фокусов которого располагается Солнце; второй закон: радиус-вектор планеты за равное время описывают одинаковые площади), однако они все...
Расчет биэллиптических траекторий космических аппаратов...
Гравитация – это преобладающая сила во Вселенной. Она проявляется и в малых и в больших масштабах. Гравитация нужна нам, чтоб оставаться на Земле, она нужна, чтоб мы могли бегать и прыгать. Например, горнолыжник использует её силу, чтоб спуститься с горы.
История зарождения и развития классической и неклассической...
Механика Ньютона стала классическим образцом дедуктивной научной теории.
Он подверг экспериментальной критике схему рефлекса как дуги, в которой центростремительные нервы благодаря связи с центробежными производят одну и ту же стандартную мышечную реакцию.
Нахождение сил и моментов в кинематических деревьях тел
В работе рассматривается задача нахождения сил и моментов в кинематическом дереве
Получены замкнутые аналитические выражения сил и моментов через динамические структуры тел.
— радиус-вектор относительно центра масс тела произвольно выбираемой точки...
Астрономия как наука в системе современного естествознания...
Успехи небесной механики | «Молодой. Данная работа посвящена определению и становлению такой науки как небесная механика, философско-научным взаимосвязям между небесной механикой и астрономическими науками. Небесная механика (англ. celestial mechanics)...
Похожие статьи
От кинематических законов Галилея и Кеплера к динамическим...
Для поддержания равномерного прямолинейного движения сила не нужна (Галилей). Для осуществления остальных видов движений (по отношению к ним суждения Аристотеля справедливы) необходима сила, которая определяется формулой (второй закон Ньютона)
Успехи небесной механики | Статья в журнале «Юный ученый»
Небесная механика (англ. celestial mechanics) — раздел астрономии, применяющий законы механики для изучения движения небесных тел. Небесная механика занимается вычислением положения Луны и планет, места и времени затмений...
Моделирование движения космических тел для исследования...
Моделирование движения произвольного количества тел в космосе — Земли, Луны и
Для этого в центр масс поместим условную звезду, с массой равной сумме масс Сириуса A и
Теперь точно так же запустим планеты, оставив в центре планетарной две звезды: Сириус A и...
К механизму взаимодействия гравитации и массы
Успехи небесной механики | «Молодой. Разработка общих вопросов движения небесных тел в гравитационном поле.
Простейшую модель центрального поля шара построил Ньютон.
Отдельно изучается сила тяжести как сила, действующая со стороны Земли на любое тело...
Использование библиотеки SFML для визуализации результатов...
Небесная механика также включает в себя законы Кеплера (первый закон: орбита планеты имеют форму эллипса, в одном из фокусов которого располагается Солнце; второй закон: радиус-вектор планеты за равное время описывают одинаковые площади), однако они все...
Расчет биэллиптических траекторий космических аппаратов...
Гравитация – это преобладающая сила во Вселенной. Она проявляется и в малых и в больших масштабах. Гравитация нужна нам, чтоб оставаться на Земле, она нужна, чтоб мы могли бегать и прыгать. Например, горнолыжник использует её силу, чтоб спуститься с горы.
История зарождения и развития классической и неклассической...
Механика Ньютона стала классическим образцом дедуктивной научной теории.
Он подверг экспериментальной критике схему рефлекса как дуги, в которой центростремительные нервы благодаря связи с центробежными производят одну и ту же стандартную мышечную реакцию.
Нахождение сил и моментов в кинематических деревьях тел
В работе рассматривается задача нахождения сил и моментов в кинематическом дереве
Получены замкнутые аналитические выражения сил и моментов через динамические структуры тел.
— радиус-вектор относительно центра масс тела произвольно выбираемой точки...
Астрономия как наука в системе современного естествознания...
Успехи небесной механики | «Молодой. Данная работа посвящена определению и становлению такой науки как небесная механика, философско-научным взаимосвязям между небесной механикой и астрономическими науками. Небесная механика (англ. celestial mechanics)...