Реализация новых технологий WolframAlpha в исследовании феномена «потребление»
Автор: Власов Дмитрий Анатольевич
Рубрика: Общие вопросы экономических наук
Опубликовано в Вопросы экономики и управления №1 (8) февраль 2017 г.
Дата публикации: 28.01.2017
Статья просмотрена: 24 раза
Библиографическое описание:
Власов, Д. А. Реализация новых технологий WolframAlpha в исследовании феномена «потребление» / Д. А. Власов. — Текст : непосредственный // Вопросы экономики и управления. — 2017. — № 1 (8). — С. 69-72. — URL: https://moluch.ru/th/5/archive/51/1932/ (дата обращения: 27.10.2024).
В центре внимания статьи — практическая реализация модели Дж. Кейнса, целью которой является исследование зависимости потребления от дохода. Раскрыты прикладные возможности использования современной базы знаний и набора вычислительных алгоритмов WolframAlpha в построении и исследовании элементарных эконометрических моделей.
Ключевые слова: доход, потребление, модель, линейная модель, предельная склонность к потреблению, регрессия, коэффициент детерминации
Цель данной статьи — демонстрация исследовательских и методических возможностей новой базы знаний и набора вычислительных алгоритмов WolframAlpha [3, 9] на примере исследования зависимости потребления от спроса. Среди положений модели Дж. Кейнса выделим следующие: «Зависимость» (гипотеза о том, что потребление зависит от дохода), «Вид зависимости» (гипотеза о линейной зависимости потребления от дохода) [8]. В качестве математического аппарата будем использовать парную линейную регрессию [14, 15], в качестве инструментального средства реализации исследования социально-экономической ситуации — WolframAlpha.
Введем обозначения: x — доход, y — потребление, ![]() — вид зависимости. Остановимся на содержательном смысле коэффициентов
— вид зависимости. Остановимся на содержательном смысле коэффициентов ![]() . Величина
. Величина ![]() ,
,![]() называется предельной склонностью к потреблению. Пусть
называется предельной склонностью к потреблению. Пусть ![]() — начальное потребление, соответствующее начальному доходу
— начальное потребление, соответствующее начальному доходу ![]() . Дадим
. Дадим ![]() приращение 1, т. е.
приращение 1, т. е. ![]() . Проследим изменение параметра
. Проследим изменение параметра ![]() . Имеем:
. Имеем: ![]() . Таким образом потребление изменилось на величину
. Таким образом потребление изменилось на величину ![]() . Величина
. Величина ![]() показывает уровень потребления при нулевом доходе. С целью верификации построенной эконометрической модели WolframAlpha предлагает использовать коэффициент детерминации и приведенный коэффициент. Этого вполне достаточно для базового уровня прикладной математической подготовки бакалавра в рамках учебной дисциплины «Эконометрика: базовый уровень» [4].
показывает уровень потребления при нулевом доходе. С целью верификации построенной эконометрической модели WolframAlpha предлагает использовать коэффициент детерминации и приведенный коэффициент. Этого вполне достаточно для базового уровня прикладной математической подготовки бакалавра в рамках учебной дисциплины «Эконометрика: базовый уровень» [4].
В настоящей статье мы демонстрируем фрагменты проведенного исследования (в полном исследовании принимало по 100 человек каждой группы) и возможности современных информационных технологий WolframAlpha. Отметим, что выделенные особенности трех групп в полном и фрагментарном исследовании отличаются несущественно. С целью исследования различий в уровне предельной склонности к потреблению и потреблению при отсутствии дохода (ожидаемое потребление) мы разделили всех участников исследования на 3 группы: неработающие пенсионеры; студенты и молодые специалисты до 35 лет; работающие специалисты старше 35 лет.
Таблица 1
Фрагмент данных для построения модели Дж. Кейнса
|
1 группа |
x |
14759 |
14570 |
17910 |
18352 |
19780 |
Средний доход 14234,1 Среднее потребление 11524,3 |
|
y |
11972 |
9790 |
14289 |
13320 |
13815 |
||
|
x |
13322 |
12254 |
11003 |
10517 |
9874 |
||
|
y |
11407 |
10132 |
10266 |
10412 |
9840 |
||
|
2 группа |
x |
3120 |
10560 |
23158 |
40300 |
61245 |
Средний доход 38298,7 Среднее потребление 38840,9 |
|
y |
9861 |
20322 |
38230 |
35554 |
56310 |
||
|
x |
42566 |
5250 |
80436 |
75552 |
40800 |
||
|
y |
42107 |
11500 |
60255 |
74350 |
39920 |
||
|
3 группа |
x |
25417 |
27320 |
31249 |
40050 |
46420 |
Средний доход 44156,1 Среднее потребление 34953,7 |
|
y |
24321 |
25800 |
28320 |
32005 |
38120 |
||
|
x |
50050 |
56884 |
65300 |
49220 |
49651 |
||
|
y |
35278 |
45210 |
50533 |
40000 |
29950 |
Таблица 1 содержит фрагмент данных по участникам каждой из трех групп, а также средний доход и среднее потребление. Отметим, что в условиях сложной финансово-экономической ситуации в России двадцать два месяца подряд снижаются доходы и потребление. Следует констатировать и изменение предельной склонности к потреблению, хотя это более устойчивая характеристика, связанная с социально-психологическими аспектами потребления, изменение которой не происходит за несколько месяцев.
Для анализа зависимости потребления от уровня дохода по первой группе, используем запрос linear fit. Полученный результат представим на рис. 1.
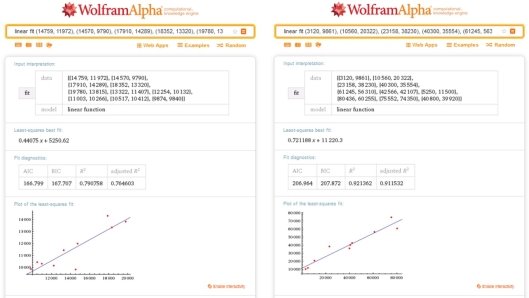
Рис. 1. Результаты анализа данных по 1 и 2 группам
Найденная зависимость имеет вид ![]() . Предельная склонность к потреблению по первой группе составляет
. Предельная склонность к потреблению по первой группе составляет ![]() , что свидетельствует о низком уровне склонности кпотреблению у неработающих пенсионеров. Потребление при нулевом доходе согласно найденной зависимости составляет
, что свидетельствует о низком уровне склонности кпотреблению у неработающих пенсионеров. Потребление при нулевом доходе согласно найденной зависимости составляет ![]() .
.
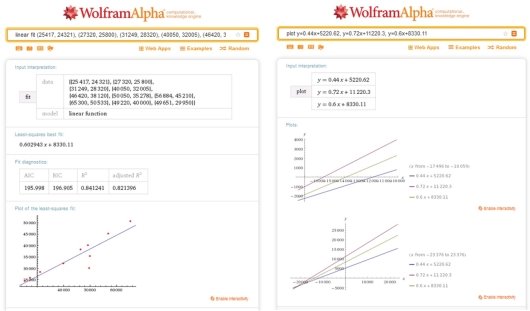
Рис. 2. Результаты анализа данных по 3 группе и визуализация найденных зависимостей
Рассмотрим далее вторую группу, состоящую из студентов и молодых специалистов до 35 лет. Для этой группы характерен большой разброс дохода: доход неработающих студентов ограничен размером получаемой стипендии, доход молодых специалистов до 35 лет может быть достаточно высоким. Уравнение линейной регрессии имеет вид: ![]() . Коэффициент
. Коэффициент ![]() свидетельствует о высоком уровне предельной склонности кпотреблению у членов этой группы. Вторая группа характеризуется также повышенным потреблением при нулевом доходе, который составляет 11220 руб. 30 коп. это свидетельствует о часто завышенных ожиданиях молодых специалистов, только что закончивших обучение.
свидетельствует о высоком уровне предельной склонности кпотреблению у членов этой группы. Вторая группа характеризуется также повышенным потреблением при нулевом доходе, который составляет 11220 руб. 30 коп. это свидетельствует о часто завышенных ожиданиях молодых специалистов, только что закончивших обучение.
Для третьей группы получаем ![]() . Коэффициент
. Коэффициент ![]() свидетельствует о среднем уровне предельной склонности кпотреблению у членов этой группы. Группа работающих специалистов старше 35 лет характеризуется также средним потреблением при нулевом доходе, который составляет 8330 руб. 11 коп.
свидетельствует о среднем уровне предельной склонности кпотреблению у членов этой группы. Группа работающих специалистов старше 35 лет характеризуется также средним потреблением при нулевом доходе, который составляет 8330 руб. 11 коп.
Выводы.
- WolframAlpha обладает мощным исследовательским идидактическим потенциалом, позволяющим по новому реализовывать прикладную математическую подготовки бакалавра экономики [10, 12], существенно обновить содержание прикладной математической подготовки за счёт расширения класса прикладных задач [6, 7], визуализировать экономические проблемы и ситуации [5, 13], исключить рутинные вычисления и приблизить учебную деятельность к профессиональной благодаря современным информационным технологиям [1], обеспечивая реализацию прикладной направленности обучения математике [11].
- Выявлены существенные отличия вособенностях потребления трех исследуемых групп (средний доход и среднее потребление, уровень склонности к потреблению, потребление при нулевом доходе). Указанные отличия могут быть использованы в процессе принятии решений [2], выработки оптимальной стратегии.
Литература:
- Власов Д. А. Информационные технологии в системе математической подготовки бакалавров: опыт МГГУ им. М. А. Шолохова // Информатика и образование. — 2012. — № 3. С. 93–94.
- Власов Д. А. Методологические аспекты принятия решений // Молодой ученый. — 2016. — № 4. — С. 760–763.
- Власов Д. А. Новое инструментальное средство WolframAlpha в исследовании экономических проблем и ситуаций // Инновационная наука. — 2016. — № 11–1. — С. 31–32.
- Власов Д. А. Технологии WolframAlpha в преподавании учебной дисциплины «Эконометрика: базовый уровень» для студентов экономического бакалавриата // Вестник Российского университета дружбы народов. Серия: Информатизация образования. — 2016. — № 4. — С. 37–47.
- Власов Д. А. Технология визуализации проблем и ситуаций финансовой сферы // Педагогика высшей школы. — 2016. — № 2. — С. 35–38.
- Власов Д. А. Типовые задачи образовательной области «Финансовая математика» для учащихся школ // Школьная педагогика. — 2016. — № 4. — С. 23–26.
- Власов Д. А., Синчуков А. В. Новое содержание прикладной математической подготовки бакалавра // Преподаватель XXI век. — 2013. — Т. 1 № 1. — С. 71–79.
- Джон Мейнард Кейнс Общая теория занятости, процента и денег — М.: Гелиос АРВ, 2015–352 с.
- Качалова Г. А., Власов Д. А. Технологии Wolframalpha при изучении элементов прикладной математики студентами бакалавриата // Молодой ученый. — 2013. — № 6. — С. 683–691.
- Синчуков А. В. Анализ перспективных направлений модернизации математической подготовки бакалавра // Инновационная наука. — 2016. — № 10–1. — С. 118–119.
- Синчуков А. В. Проблемы реализации прикладной направленности обучения математике с использованием информационных технологий // Инновационная наука. — 2016. — № 10–1. — С. 116–118.
- Синчуков А. В. Современная классификация математических моделей // Инновационная наука. — 2016. — № 3–1. — С. 214–215.
- Синчуков А. В. Технологическое проектирование содержания математической подготовки бакалавра менеджмента // Молодой ученый. — 2016. — № 20. — С. 730–732.
- Тихомиров Н. П., Дорохина Е. Ю. Эконометрика. — М.: Изд-во Рос. экон. акад., 2002. — 640 с.
- Тихомиров Н. П., Тихомирова Т. М. Методы эконометрики и многомерного статистического анализа. — М.: Экономика, 2010. — 636 с.
Ключевые слова
модель, потребление, доход, доход, регрессия, линейная модель, предельная склонность к потреблению, коэффициент детерминацииПохожие статьи
Аналитическое сравнение рекуррентных моделей в задаче прогнозирования динамики ценных бумаг
В данной статье рассматриваются подходы машинного обучения в задаче анализа и прогнозирования рынка ценных бумаг. В работе сравниваются такие аспекты, как количество занимаемой памяти, число параметров, а также величина затраченного на обучение модел...
Современная фрактальная теория: визуализация и прикладные аспекты
В центре внимания статьи — современная фрактальная теория, одно из перспективных направлений, используемых для анализа социально-экономических проблем и ситуаций. Представлены примеры визуализации фракталов в базе знаний и наборе вычислительных алгор...
Моделирование динамики заработной платы в Российской Федерации
В рамках модели лагов Алмон рассмотрено влияние инвестиций в основной капитал в Российской Феде-рации на уровень заработной платы. Выбиралась линейная и квадратичная структура лага. Приведены модельные соотношения и результаты их анализа в среде MATL...
Математическое моделирование как инструмент развития социоэкономики
В статье рассматриваются возможности применения математического моделирования для решения задач социоэкономики. Анализируются основные этапы моделирования, а также особенности моделирования социально-экономических процессов. Рассматриваются примеры н...
Профилактика конфликтного поведения у подростков
Данная статья исследования состоит в предположении о том, что проведение тренинговых занятий способствует снижению уровня склонности подростков к конфликтному поведению и выбору ими оптимальных стратегий поведения в конфликтных ситуациях. Методами ис...
Статистический анализ денежных потоков и стоимостных факторов в целях управления стоимостью корпорации
В статье предложена методика статистического анализа, рассматривающая корреляционную связь между распределением денежных потоков предприятия и величинами различных ставок дисконтирования. В зависимости от цели анализа и полученных выводов, описанный ...
Перспективы развития предпринимательской деятельности на рынке электробытовой техники
В статье исследуется проблема анализа качества медицинской помощи, для чего используется комплекс статистических методов: анализ динамики, вариации, построение линейный и нелинейных моделей аппроксимации.
Модификация теории социального влияния Латане для компьютерных социальных сетей
Данная статья посвящена проблемам анализа межличностных отношений в компьютерных социальных сетях. Речь идет об использовании теории динамического социального влияния Латане на основе различных характеристик (количественных и структурных), понятий, м...
Сферы применения искусственного интеллекта в бизнесе России
В статье автор рассматривает возможные сферы применения искусственного интеллекта в различных бизнесах в России. Для исследования были использованы статистические данные опросов, проведенных «Инфосистемы Джет» и «Tadviser». Также проанализированы осн...
Кибернетика распределенных реестров на технологиях блокчейна
В статье автор строит модель блокчейн сети, основанной на «доказательстве работы» (PoW). Проведен математический анализ модели. Выполнено численное моделирование работы сети при различном количестве участников. Применена линейная регрессия для собран...
Похожие статьи
Аналитическое сравнение рекуррентных моделей в задаче прогнозирования динамики ценных бумаг
В данной статье рассматриваются подходы машинного обучения в задаче анализа и прогнозирования рынка ценных бумаг. В работе сравниваются такие аспекты, как количество занимаемой памяти, число параметров, а также величина затраченного на обучение модел...
Современная фрактальная теория: визуализация и прикладные аспекты
В центре внимания статьи — современная фрактальная теория, одно из перспективных направлений, используемых для анализа социально-экономических проблем и ситуаций. Представлены примеры визуализации фракталов в базе знаний и наборе вычислительных алгор...
Моделирование динамики заработной платы в Российской Федерации
В рамках модели лагов Алмон рассмотрено влияние инвестиций в основной капитал в Российской Феде-рации на уровень заработной платы. Выбиралась линейная и квадратичная структура лага. Приведены модельные соотношения и результаты их анализа в среде MATL...
Математическое моделирование как инструмент развития социоэкономики
В статье рассматриваются возможности применения математического моделирования для решения задач социоэкономики. Анализируются основные этапы моделирования, а также особенности моделирования социально-экономических процессов. Рассматриваются примеры н...
Профилактика конфликтного поведения у подростков
Данная статья исследования состоит в предположении о том, что проведение тренинговых занятий способствует снижению уровня склонности подростков к конфликтному поведению и выбору ими оптимальных стратегий поведения в конфликтных ситуациях. Методами ис...
Статистический анализ денежных потоков и стоимостных факторов в целях управления стоимостью корпорации
В статье предложена методика статистического анализа, рассматривающая корреляционную связь между распределением денежных потоков предприятия и величинами различных ставок дисконтирования. В зависимости от цели анализа и полученных выводов, описанный ...
Перспективы развития предпринимательской деятельности на рынке электробытовой техники
В статье исследуется проблема анализа качества медицинской помощи, для чего используется комплекс статистических методов: анализ динамики, вариации, построение линейный и нелинейных моделей аппроксимации.
Модификация теории социального влияния Латане для компьютерных социальных сетей
Данная статья посвящена проблемам анализа межличностных отношений в компьютерных социальных сетях. Речь идет об использовании теории динамического социального влияния Латане на основе различных характеристик (количественных и структурных), понятий, м...
Сферы применения искусственного интеллекта в бизнесе России
В статье автор рассматривает возможные сферы применения искусственного интеллекта в различных бизнесах в России. Для исследования были использованы статистические данные опросов, проведенных «Инфосистемы Джет» и «Tadviser». Также проанализированы осн...
Кибернетика распределенных реестров на технологиях блокчейна
В статье автор строит модель блокчейн сети, основанной на «доказательстве работы» (PoW). Проведен математический анализ модели. Выполнено численное моделирование работы сети при различном количестве участников. Применена линейная регрессия для собран...







