Задача о назначении с дополнительными работами и исполнителями
Авторы: Кузовлев Дмитрий Игоревич, Тизик Александр Петрович, Тресков Юрий Павлович
Рубрика: 1. Информатика и кибернетика
Опубликовано в
II международная научная конференция «Технические науки в России и за рубежом» (Москва, ноябрь 2012)
Статья просмотрена: 1054 раза
Библиографическое описание:
Кузовлев, Д. И. Задача о назначении с дополнительными работами и исполнителями / Д. И. Кузовлев, А. П. Тизик, Ю. П. Тресков. — Текст : непосредственный // Технические науки в России и за рубежом : материалы II Междунар. науч. конф. (г. Москва, ноябрь 2012 г.). — Москва : Буки-Веди, 2012. — С. 16-18. — URL: https://moluch.ru/conf/tech/archive/55/2866/ (дата обращения: 27.07.2024).
- Предложен новый метод решения задачи о назначении, основанный на
декомпозиции исходной задачи на ряд двумерных оптимизационных задач.
Целочисленность и монотонность по целевой функции итерационного
процесса решения обеспечивает конечность алгоритма. В результате
может получиться или единственное оптимальное решение исходной
задачи о назначении, или система ограничений, из которой можно
получить все оптимальные решения.
- Введение. В [1] предлагается метод решения классической транспортной задачи, основанный на декомпозиции исходной задачи на последовательность двумерных задач с последовательно модифицируемыми целевыми функциями. В настоящей работе метод распространяется на случай задачи о назначении, когда имеются дополнительные работы и исполнители, а затраты линейно зависят от соответствующих слабых переменных. Тем самым, алгоритм [1] напрямую переносится на важный класс нелинейных задач транспортного типа.
- 1. Постановка задачи. Имеется, как и в обычной задаче о назначении n работ и n исполнителей. Стоимость выполнения
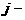 ой
работы
ой
работы
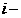 ым
исполнителем равна
ым
исполнителем равна
 .
Кроме того, имеются еще n дополнительных работ. Каждую
.
Кроме того, имеются еще n дополнительных работ. Каждую
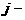 ую
дополнительную работу может выполнять только
ую
дополнительную работу может выполнять только
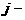 й
исполнитель. Имеется также n дополнительных исполнителей. Каждый
й
исполнитель. Имеется также n дополнительных исполнителей. Каждый
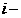 ый
дополнительный исполнитель может выполнять только
ый
дополнительный исполнитель может выполнять только
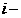 ую
(обычную, не дополнительную работу). Стоимость выполнения
ую
(обычную, не дополнительную работу). Стоимость выполнения
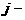 й
дополнительной работы равна
й
дополнительной работы равна
 ,
стоимость работы
,
стоимость работы
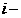 го
дополнительного исполнителя
го
дополнительного исполнителя
 .
Задача состоит в минимизации общей стоимости выполнения работ при
обеспечении выполнения всех обычных работ.
.
Задача состоит в минимизации общей стоимости выполнения работ при
обеспечении выполнения всех обычных работ.- Формальная запись задачи:
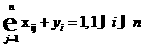 (1)
(1)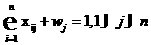 (2)
(2)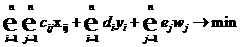 (3)
(3) - принимают значения нуль или единица. (4)
- принимают значения нуль или единица. (4)- Кроме того, будем считать
 четными числами, что не ограничивает общности рассмотрения.
четными числами, что не ограничивает общности рассмотрения.- 2. Метод решения задачи. Положим
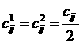 и образуем 2n оптимизационных задач с одним ограничением. Первый
этап. Сформируем одномерных задач.
и образуем 2n оптимизационных задач с одним ограничением. Первый
этап. Сформируем одномерных задач.- Первые n оптимизационных задач:
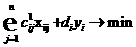 (5)
(5)- при ограничениях (4) и при
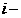 м ограничении из (1),
м ограничении из (1),
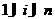 .
.- Вторые n оптимизационных задач:
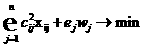 (6)
(6)- при ограничениях (4) и при
 м ограничении из (2),
м ограничении из (2),
 .
.- Задачи вида (1), (4), (5) и (2), (4), (6) решаются простым выбором переменной, у которой целевой функции минимальный коэффициент. Если минимальных коэффициентов несколько, то в качестве решения записывается, что сумма соответствующих переменных равна единице.
- Если объединение оптимальных решений всех 2n задач (1), (4), (5) и (2), (4), (6) является допустимым решением задачи (1) – (4), то оно является оптимальным решением задачи (1) – (4).
- В противном случае начинается итерационный процесс решения
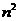 оптимизационных задач с двумя ограничениями – по одному
ограничению из (1) и (2) и с целевой функцией, в которой из (3)
присутствуют только переменные, которые имеются в выбранных
ограничениях. Первая задача с двумя ограничениями запишется:
оптимизационных задач с двумя ограничениями – по одному
ограничению из (1) и (2) и с целевой функцией, в которой из (3)
присутствуют только переменные, которые имеются в выбранных
ограничениях. Первая задача с двумя ограничениями запишется: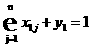 (7)
(7)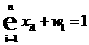 (8)
(8) (9)
(9)- при ограничениях (4).
- Если
 ,
то оптимальным решением задачи (4), (7)-(9) будет
,
то оптимальным решением задачи (4), (7)-(9) будет
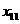 .
.- Если
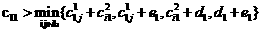 ,
то в оптимальное решение задачи (4), (7)-(9) со значением 1 войдут
переменные с индексами, на которых реализуется
,
то в оптимальное решение задачи (4), (7)-(9) со значением 1 войдут
переменные с индексами, на которых реализуется
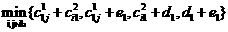
- Если
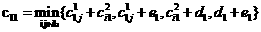 ,
,- то в качестве решения в обоих ограничениях записывается
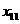 в сумме той переменной, с индексом которой реализуется выписанный
минимум.
в сумме той переменной, с индексом которой реализуется выписанный
минимум.- После решения задачи пересчитываются
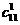 и
и
 .
Если
.
Если
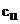 меньше соответствующего минимума (для определенности пусть это будет
меньше соответствующего минимума (для определенности пусть это будет
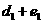 ),
то получаем
),
то получаем
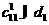 и
и
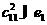 .
Если
.
Если
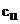 равно минимуму, то полагаем
равно минимуму, то полагаем
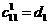 и
и
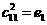 .
Если
.
Если
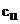 больше минимуму, то полагаем
больше минимуму, то полагаем
 и
и
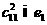 .
Всегда можно сделать это так, что
.
Всегда можно сделать это так, что
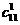 и
и
 будут целыми числами. Описанные значения величин
будут целыми числами. Описанные значения величин
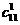 и
и
 обеспечивают совпадение объединения оптимальных решений двух задач с
одним ограничением с оптимальным решением задачи с двумя
ограничениями.
обеспечивают совпадение объединения оптимальных решений двух задач с
одним ограничением с оптимальным решением задачи с двумя
ограничениями.- Так же, как и в общем случае обобщенной транспортной задачи [1], имеет место монотонное возрастание суммы значений целевых функций всех
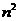 задач с двумя ограничениями. В силу ограниченности и целочисленности
процесса предел достигается за конечное число шагов. Если по
достижении предела объединения оптимальных решений задач с одним
ограничением является допустимым решением задачи (1)-(4), то тем
самым получено оптимальное решение исходной задачи (1)-(4).
задач с двумя ограничениями. В силу ограниченности и целочисленности
процесса предел достигается за конечное число шагов. Если по
достижении предела объединения оптимальных решений задач с одним
ограничением является допустимым решением задачи (1)-(4), то тем
самым получено оптимальное решение исходной задачи (1)-(4).- Предельное состояние множества задач с одним ограничением не обязательно непосредственно позволяет получить оптимальное решение исходной задачи. Такую ситуацию назовем вырождением. Вопросы вырождения рассматривали в [1]. Вырождение имеет место и в приводимом ниже примере. Состояние вырожденности преодолевается дополнительными процедурами.
- 3. Пример. Имеется 5 обычных работ и 5 обычных исполнителей. Кроме того, имеется 5 дополнительных работ, не обязательных для выполнения, и 5 дополнительных исполнителей, которым не обязательно предоставлять работу. Необходимо минимизировать общие расходы при выполнении всех обычных работ и предоставлении работы всем обычным исполнителям. Формальная запись задачи:

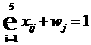 ,
, 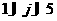
 Объединение
оптимальных решений задач с одним ограничением не является
допустимым решением исходной задачи
Объединение
оптимальных решений задач с одним ограничением не является
допустимым решением исходной задачи- Далее решаются задачи с двумерными ограничениями вида:
- 1)
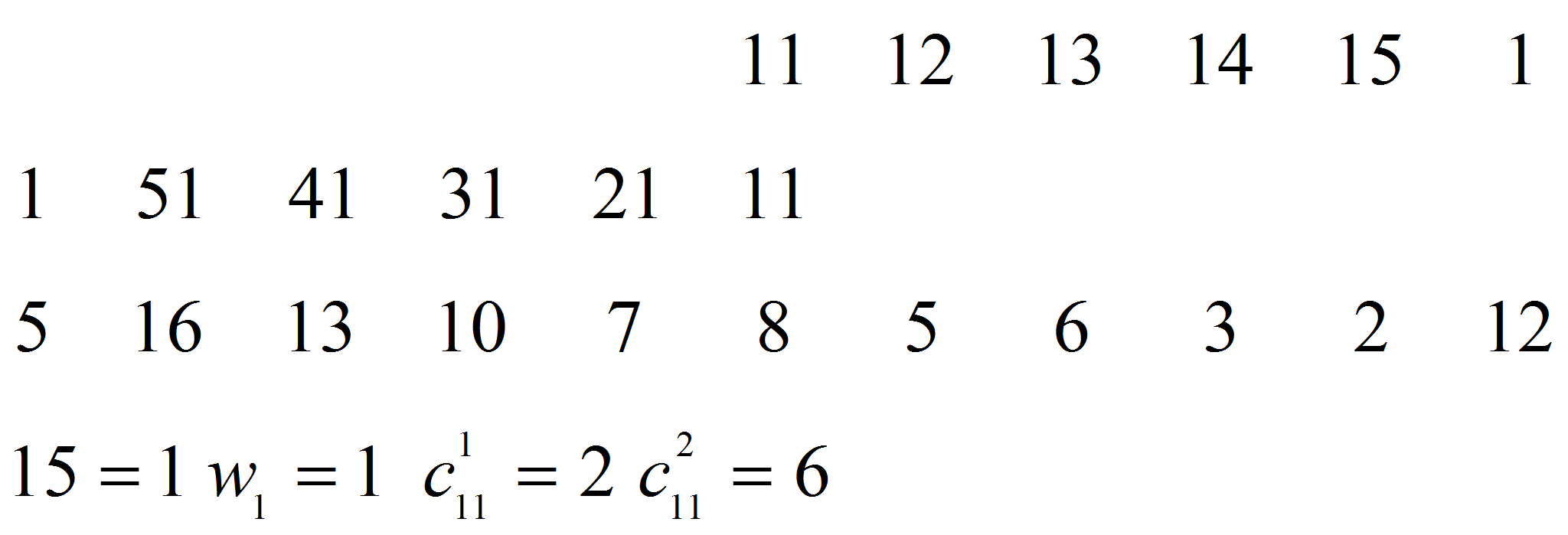
- 2)

- 3)

- 4)

- Здесь используется сокращённая запись, где фигурируют только индексы переменных. Нетрудно видеть, что допустимого решения исходной задачи сразу не получается. В частности, в первых четырёх двумерных задачах поочередно не допускаются в список на включение в решение. В этом состоянии, вообще, невозможно составить матрицу претендентов на включение в оптимальное решение. Положение, однако, легко исправляется, если в целевых функциях передать по единице из
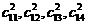 соответственно в
соответственно в
 .
.
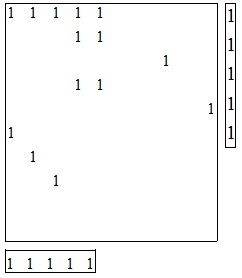
- После этого матрица претендентов на включение в решение может быть выписана:
- Введение. В [1] предлагается метод решения классической транспортной задачи, основанный на декомпозиции исходной задачи на последовательность двумерных задач с последовательно модифицируемыми целевыми функциями. В настоящей работе метод распространяется на случай задачи о назначении, когда имеются дополнительные работы и исполнители, а затраты линейно зависят от соответствующих слабых переменных. Тем самым, алгоритм [1] напрямую переносится на важный класс нелинейных задач транспортного типа.
-
В вычисленной матрице первые пять строк соответствуют пяти обычным
исполнителям. Вторые пять строк соответствуют пяти дополнительным
исполнителям. Первые пять столбцов соответствуют пяти обычным
работам, вторые – пяти дополнительным работам. Единицы стоят
на местах переменных
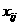 ,
,
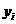 ,
,
 ,
претендующих на включение в оптимальное решение исходной задачи в
соответствии со значениями коэффициентов в задачах с одним
ограничением.
,
претендующих на включение в оптимальное решение исходной задачи в
соответствии со значениями коэффициентов в задачах с одним
ограничением.
- Нетрудно видеть, что при однозначности
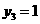 и
и
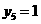 имеется ровно шесть оптимальных решений: три варианта - по два из
трех
имеется ровно шесть оптимальных решений: три варианта - по два из
трех
 ,
,
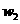 ,
,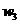 в сочетании с двумя вариантами
в сочетании с двумя вариантами
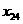 ,
,
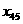 и
и
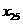 ,
,
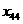 ,
например
,
например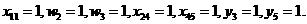
- Литература:
- Нетрудно видеть, что при однозначности
- А.П. Тизик, В.И. Цурков. Метод последовательных изменений параметров функционала для решения транспортной задачи // Автоматика и телемеханика. 2012. №1. P. 148-158.