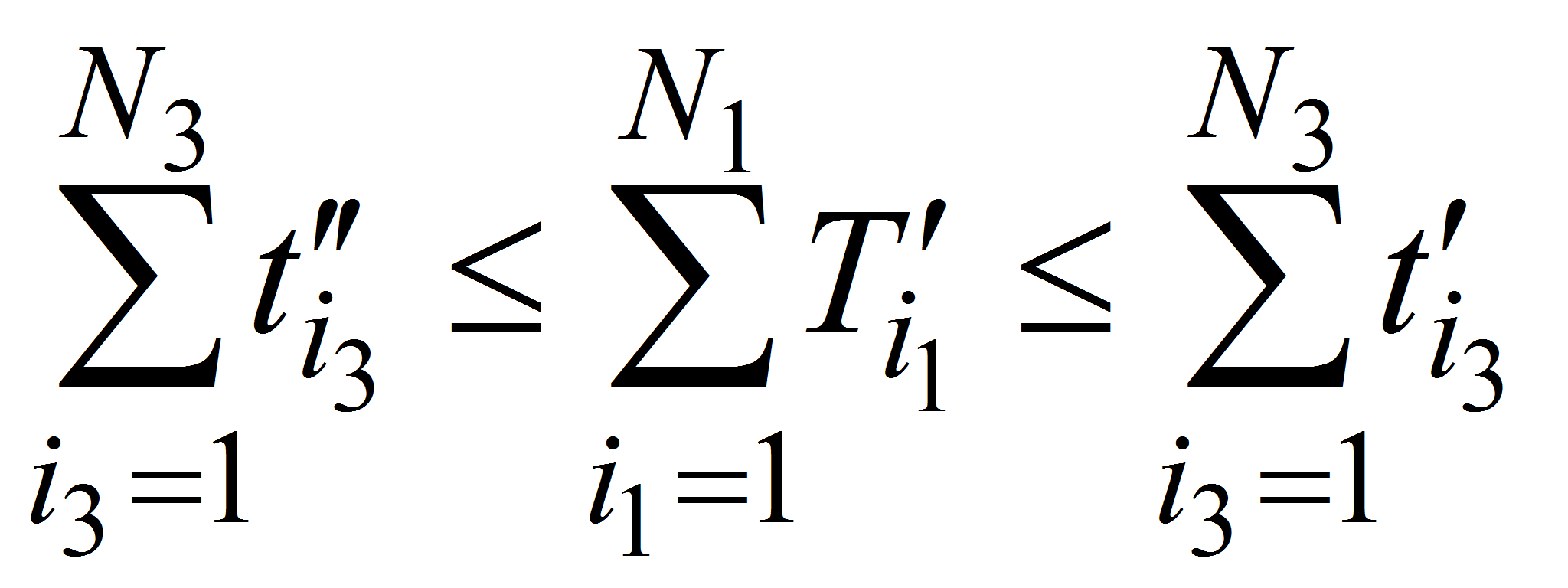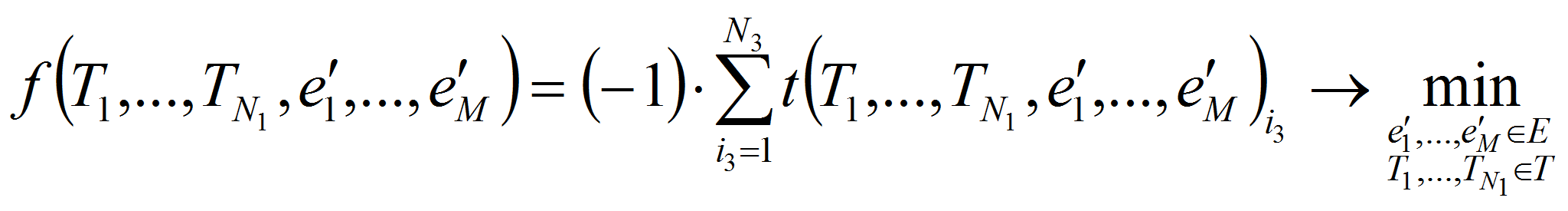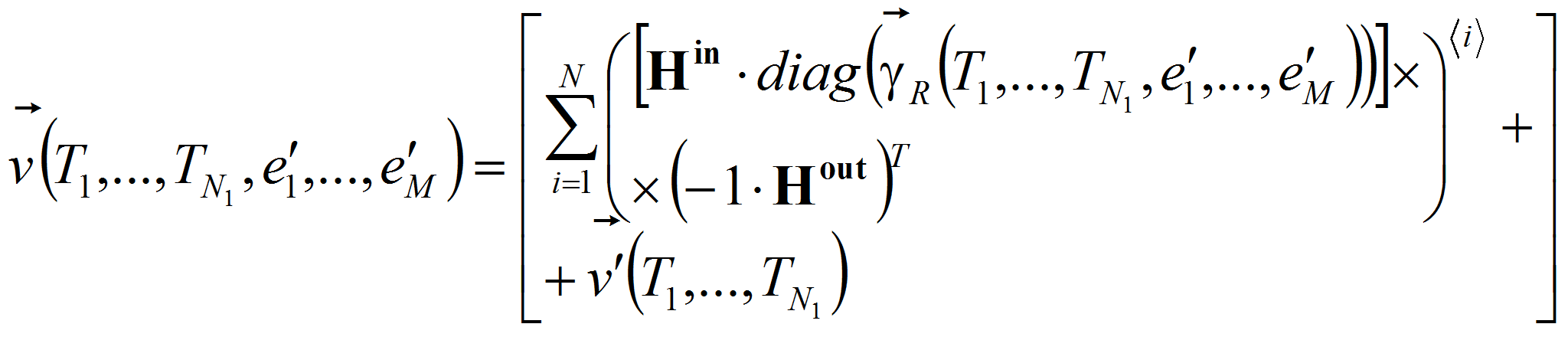Задача распределения однородных непрерывных ограниченных ресурсов в иерархических системах транспортного типа с древовидной структурой
Авторы: Полянский Иван Сергеевич, Фролов Михаил Михайлович, Лукьянченкова Наталия Евгеньевна
Рубрика: 3. Автоматика и вычислительная техника
Опубликовано в
II международная научная конференция «Технические науки в России и за рубежом» (Москва, ноябрь 2012)
Статья просмотрена: 365 раз
Библиографическое описание:
Полянский, И. С. Задача распределения однородных непрерывных ограниченных ресурсов в иерархических системах транспортного типа с древовидной структурой / И. С. Полянский, М. М. Фролов, Н. Е. Лукьянченкова. — Текст : непосредственный // Технические науки в России и за рубежом : материалы II Междунар. науч. конф. (г. Москва, ноябрь 2012 г.). — Москва : Буки-Веди, 2012. — С. 52-55. — URL: https://moluch.ru/conf/tech/archive/55/2680/ (дата обращения: 26.04.2024).
В общем
виде,
иерархическая
система транспортного типа представлена совокупностью элементов
разделяемых на три множества: 1. пункты производства; 2.
промежуточные пункты; 3. пункты потребления однородного ресурса,
функциональная взаимосвязь между которыми представлена в виде
древовидной структуры. Задача распределения однородного ограниченного
ресурса в иерархической системе транспортного типа заключается в
определении оптимального плана перевозок, обеспечивающего эффективное
функционирование системы и заключающегося в нахождении оптимальных
объемов: 1. производства
![]() ресурса
ресурса
![]() -м
пунктом производства (
-м
пунктом производства (![]() ,
где
,
где
![]() – общее число пунктов производства однородного непрерывного
ресурса в иерархической системе); 2. потребления
– общее число пунктов производства однородного непрерывного
ресурса в иерархической системе); 2. потребления
![]() ресурса
ресурса
![]() -м
пунктом потребления (
-м
пунктом потребления (![]() ,
где
,
где
![]() – общее число пунктов потребления однородного непрерывного
ресурса в иерархической системе), с учетом ограничений на: 1.
максимально допустимый объем производства
– общее число пунктов потребления однородного непрерывного
ресурса в иерархической системе), с учетом ограничений на: 1.
максимально допустимый объем производства
![]() ресурса
ресурса
![]() -м
пунктом производства; минимально и максимально допустимые объемы
потребления
-м
пунктом производства; минимально и максимально допустимые объемы
потребления
![]() и
и
![]() ресурса
ресурса
![]() -м
пунктом потребления; 3. пропускную способность
-м
пунктом потребления; 3. пропускную способность
![]() при перевозки ресурса через
при перевозки ресурса через
![]() -е
промежуточные пункты (
-е
промежуточные пункты (![]() ,
где
,
где
![]() – общее число пунктов перевозки однородного непрерывного
ресурса в иерархической системе).
– общее число пунктов перевозки однородного непрерывного
ресурса в иерархической системе).
С учетом вышесказанного, в общем виде оптимальное распределение однородного непрерывного ограниченного ресурса в иерархической системе транспортного типа с древовидной структурой является задачей параметрического синтеза иерархической системы, формальная постановка которой запишется в виде многокритериальной оптимизационной задачи:
при условии, что
в случае, когда
где
![]() – объем ресурса, поступающего на вход
– объем ресурса, поступающего на вход
![]() -го
промежуточного пункта.
-го
промежуточного пункта.
Согласно [1 –
3], представим иерархическую систему транспортного типа в виде
ориентированного связного графа
![]() без петель и параллельных рёбер (корневого ориентированного дерева)
[4], представленного совокупностью непустого множества
без петель и параллельных рёбер (корневого ориентированного дерева)
[4], представленного совокупностью непустого множества
![]() вершин и множества
вершин и множества
![]() ребер двухэлементных подмножеств множества
ребер двухэлементных подмножеств множества
![]() [5]:
[5]:
где
![]() ,
а
,
а
![]() ,
N
и M
– общее число вершин и ребер графа
соответственно. Причем, в рассматриваемой постановке задачи,
множество
,
N
и M
– общее число вершин и ребер графа
соответственно. Причем, в рассматриваемой постановке задачи,
множество
![]() вершин графа
вершин графа
![]() представлено совокупностью непересекающихся подмножеств: 1.
представлено совокупностью непересекающихся подмножеств: 1.
![]() – пунктов производства (корней ориентированного дерева); 2.
– пунктов производства (корней ориентированного дерева); 2.
![]() – промежуточных пунктов (промежуточных узлов ориентированного
дерева); 3.
– промежуточных пунктов (промежуточных узлов ориентированного
дерева); 3.
![]() – пунктов потребления (листьев ориентированного дерева), т. е.
– пунктов потребления (листьев ориентированного дерева), т. е.
![]() ,
с условием
,
с условием
![]() и
и
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Под
совокупностью (объединением) подмножеств множества вершин –
пунктов производства
![]() и промежуточных пунктов
и промежуточных пунктов
![]() будем понимать подмножество делителей
будем понимать подмножество делителей
![]() однородного непрерывного ресурса, тогда вес ребер из множества
однородного непрерывного ресурса, тогда вес ребер из множества
![]() ,
являющихся истоками из вершин подмножества
,
являющихся истоками из вершин подмножества
![]() ,
определяется величиной соответствующих коэффициентов деления с выхода
делителей
,
определяется величиной соответствующих коэффициентов деления с выхода
делителей
![]() из подмножества
из подмножества
![]() .
Обозначим через
.
Обозначим через
![]() – подмножество множества ребер графа
– подмножество множества ребер графа
![]() являющихся истоками из i-й
вершины, причем
являющихся истоками из i-й
вершины, причем
![]() и
и
![]() .
.
Тогда, с
учетом вышесказанного, задача оптимального распределения однородного
непрерывного ограниченного ресурса заключается в определении весов
ребер (коэффициентов деления) истоков из вершин подмножества
![]() по критерию
по критерию
с учетом ограничений
и
дополнительного ограничения накладываемого на коэффициенты деления
k-х
(![]() ,
где
,
где
![]() – общее число вершин графа
– общее число вершин графа
![]() ,
принадлежащих подмножеству
,
принадлежащих подмножеству
![]() ,
т.е.
,
т.е.
![]() )
делителей (веса рёбер) определяемые выражением
)
делителей (веса рёбер) определяемые выражением
где
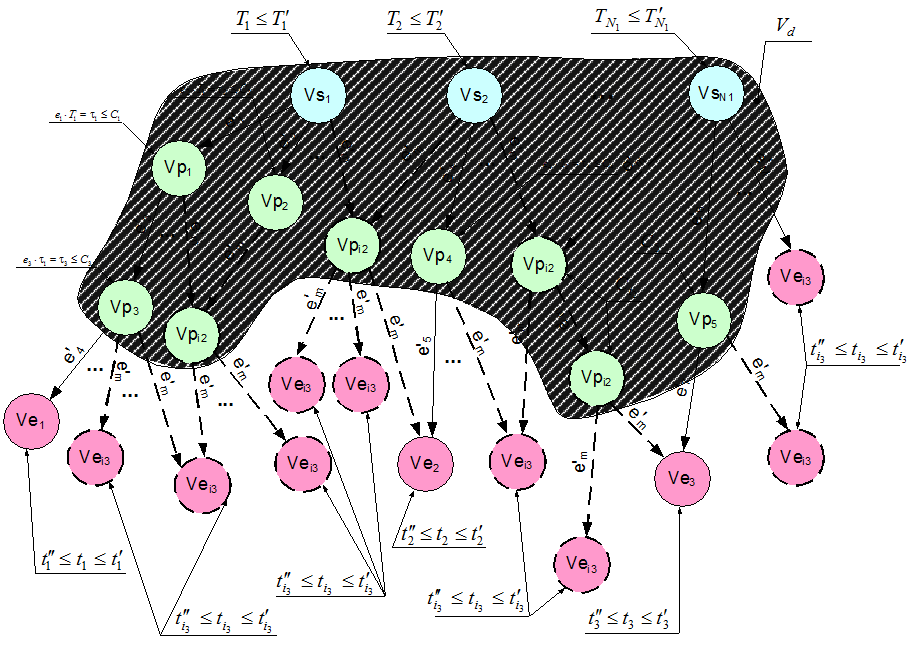
Геометрия решения задачи представлена на рисунке 1.
Для определения векторной
функции выражения (8)
![]() ,
в рассматриваемой постановке задачи, i3-й
элемент (
,
в рассматриваемой постановке задачи, i3-й
элемент (![]() )
которой характеризует величину распределяемого в i3-й
пункт потребления однородного непрерывного ресурса
)
которой характеризует величину распределяемого в i3-й
пункт потребления однородного непрерывного ресурса
![]() ,
введем следующие обозначения. Ориентированный граф
,
введем следующие обозначения. Ориентированный граф
![]() будем задавать матрицами инциденций для прямого и обратного потоков
будем задавать матрицами инциденций для прямого и обратного потоков
![]() и
и
![]() соответственно, элементы которых определяются выражениями [5]
соответственно, элементы которых определяются выражениями [5]
Рис. 1. Геометрия решения задачи распределения однородного непрерывного ограниченного ресурса в иерархической системе транспортного типа с древовидной структурой.
Для
ориентированного графа
![]() определим матрицу
определим матрицу
![]() ,
являющуюся матрицей достижимости (т. е. если vp
вершина достижима из vi,
то (i,
p)-й
элемент матрицы достижимости равен 1, в противном случае – 0,
,
являющуюся матрицей достижимости (т. е. если vp
вершина достижима из vi,
то (i,
p)-й
элемент матрицы достижимости равен 1, в противном случае – 0,
![]() )
для пути кратности r
(r
задает число ребер, проходя через которые из
vi
вершины есть путь в vp
вершину). Матрица
)
для пути кратности r
(r
задает число ребер, проходя через которые из
vi
вершины есть путь в vp
вершину). Матрица
![]() определяется равенством
определяется равенством
Поскольку
![]() является ориентированным связным графом без петель и параллельных
рёбер, то, согласно [5], величина r
ограничена значением R,
определяющим максимально-возможное число
ребер, проходя через которые существует путь из i-й
вершины в p-ю.
Величина R
определяется максимально допустимым числом переходов, для которых
норма матрицы
является ориентированным связным графом без петель и параллельных
рёбер, то, согласно [5], величина r
ограничена значением R,
определяющим максимально-возможное число
ребер, проходя через которые существует путь из i-й
вершины в p-ю.
Величина R
определяется максимально допустимым числом переходов, для которых
норма матрицы
![]() не равна нулю, т.е.
не равна нулю, т.е.
![]() ,
а
,
а
![]() .
.
Введем
векторную функцию
![]() ,
i-й
элемент (
,
i-й
элемент (![]() )
которой определяет вес i-й
вершины, т. е., в рассматриваемой постановке задачи, характеризует
объем ресурса передаваемого в i-ю
вершину графа
)
которой определяет вес i-й
вершины, т. е., в рассматриваемой постановке задачи, характеризует
объем ресурса передаваемого в i-ю
вершину графа
![]() ,
определяемую согласно выражения
,
определяемую согласно выражения
где
![]() – векторная функция, i-й
элемент (
– векторная функция, i-й
элемент (![]() )
которой определяет величину ресурса производимого i-й
вершиной графа
)
которой определяет величину ресурса производимого i-й
вершиной графа
![]() ;
;
![]() – R-я
векторная функция рассчитывается согласно рекуррентной формуле
– R-я
векторная функция рассчитывается согласно рекуррентной формуле
В выражении (16) начальное
значение функции
![]() и матричная функция
и матричная функция
![]() ,
определяются равенствами
,
определяются равенствами
Тогда элементы векторной
функции
![]() ,
принадлежащие подмножеству
,
принадлежащие подмножеству
![]() пунктов потребления ресурса множества
V
вершин графа
пунктов потребления ресурса множества
V
вершин графа
![]() ,
определяют i3-е
элементы искомой векторной функции
,
определяют i3-е
элементы искомой векторной функции
![]() минимизируемого выражения (8):
минимизируемого выражения (8):
где
![]() – вектор размерностью
– вектор размерностью
![]() ,
,
![]() -е
элементы которого определяют номера вершин графа
-е
элементы которого определяют номера вершин графа
![]() составляющих подмножество
составляющих подмножество
![]() пунктов потребления ресурса.
пунктов потребления ресурса.
Формализованную задачу распределения однородного ограниченного непрерывного ресурса в иерархической системе транспортного типа с древовидной структурой предлагается осуществлять по критерию оптимальности, путем численного решения оптимизационной задачи (8) с учетом ограничений (9), (10) и топологии (12), (13) методами второго порядка (Ньютона, Ньютона–Рафсона, Марквардта и др.) обладающими, согласно [6] и исследованию, проведенному в [7], наилучшей скоростью сходимости.
Литература:
Прилуцкий М. Х. Распределение однородного ресурса в иерархических системах древовидной структуры. Труды международной конференции «Идентификация систем и задачи управления SICPRO 2000». Москва 26-28 сентября 2000. Институт проблем управления им. В. А. Трапезникова РАН. М.: Институт проблем управления им. В. А. Трапезникова РАН, 2000, с. 2038-2049.
Прилуцкий М. Х., Картомин А. Г. Потоковые алгоритмы распределения ресурсов в иерархических системах. Электронный журнал «Исследовано в России», 39, стр. 444-452, 2003.
Афраймович Л. Г., Прилуцкий М. Х., Многоиндексные задачи распределения ресурсов в иерархических системах.//Автоматика и телемеханика, 2006, №6, с.194-205.
Бертсекас Д., Галлагер Р. Сети передачи данных. – М.: Мир, 1989. – 544 с.
Новиков Ф.А. Дискретная математика для программистов: Учебник для вузов. 3-е изд. – СПб.: Питер, 2008. – 384 с.: ил.
Полак Э. Численные методы оптимизации. Единый подход. : Пер. с английского Ф. И. Ерешко / Под ред. И.А. Вателя. – М., "Мир", 1974. – 376 с.
Химмельблау Д. Прикладное нелинейное программирование. – М.: изд. «МИР», 1975. – 536 с.