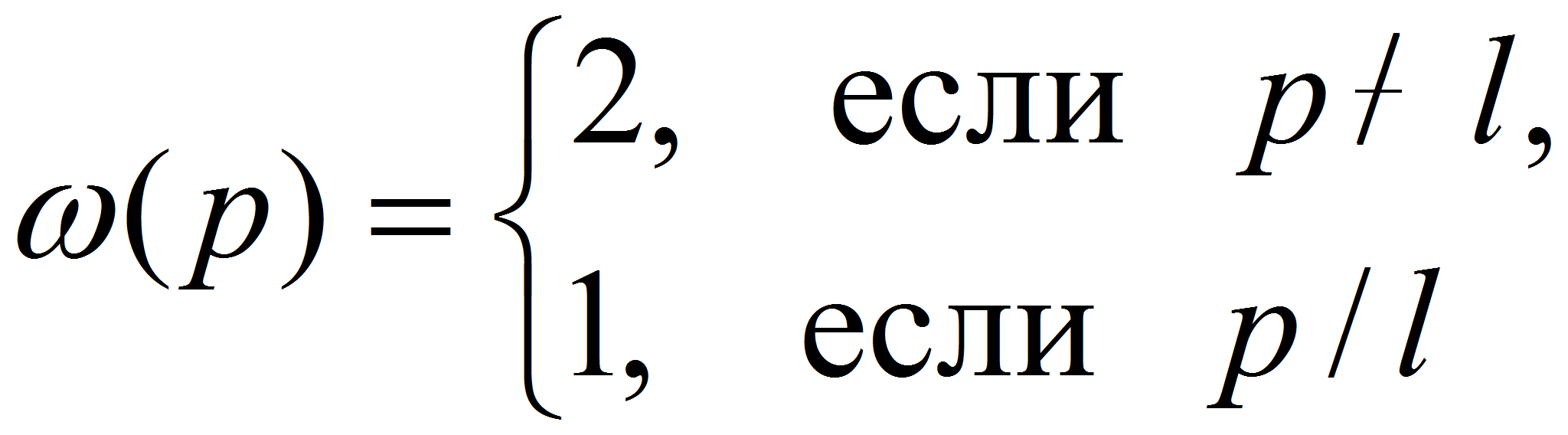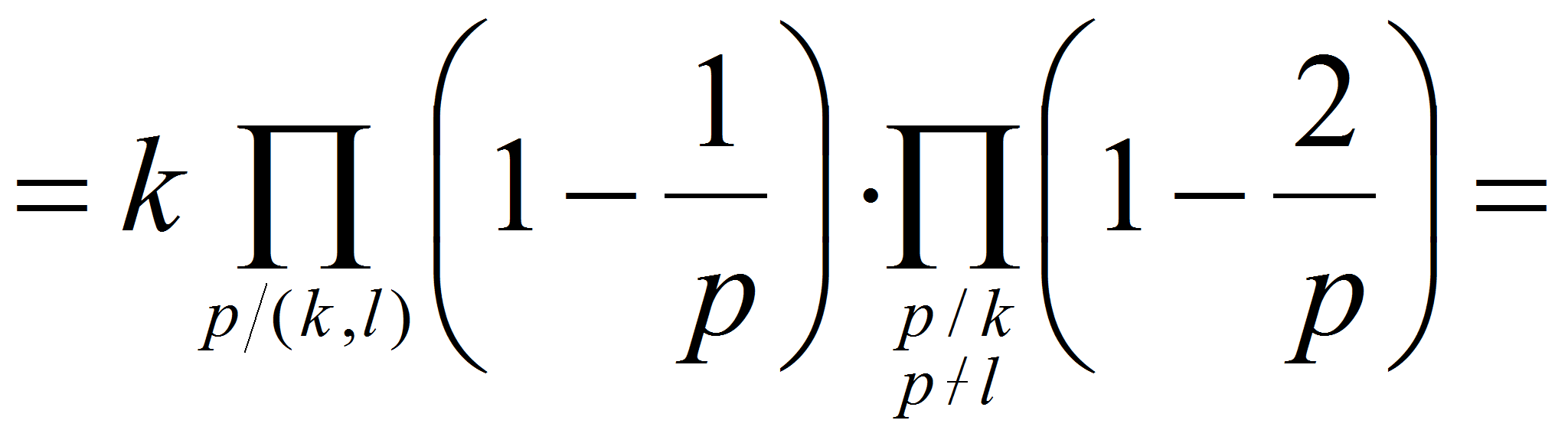Условия нулевой плотности множеств натуральных чисел в арифметических прогрессиях, представимых в виде p+am
Автор: Оразов Мамед
Рубрика: 14. Общие вопросы технических наук
Опубликовано в
международная научная конференция «Современные тенденции технических наук» (Уфа, октябрь 2011)
Статья просмотрена: 150 раз
Библиографическое описание:
Оразов, Мамед. Условия нулевой плотности множеств натуральных чисел в арифметических прогрессиях, представимых в виде p+am / Мамед Оразов. — Текст : непосредственный // Современные тенденции технических наук : материалы I Междунар. науч. конф. (г. Уфа, октябрь 2011 г.). — Уфа : Лето, 2011. — С. 67-68. — URL: https://moluch.ru/conf/tech/archive/5/947/ (дата обращения: 26.04.2024).
Рассматривается
задача о представлении натуральных чисел, при надлежащих заданному
классу вычетов по некоторому модулю и представимых в виде суммы u+v,
где u,v-
члены двух заданных
последовательностей натуральных чисел. В 1934 году Н.П.Романов
доказал теорему о положительной плотности множеств натуральных чисел
представимых в виде![]() где
p-
пробегает простые числа, m-
натуральные число. В данной работе
рассматривается
анолагичная задача на случай, когда представимые
числа принадлежат арифметической прогрессии по заданному модулю k.
Кроме того полечены достаточные условия для того, чтобы числа
некоторых арифметической прогрессии
представимые виде
где
p-
пробегает простые числа, m-
натуральные число. В данной работе
рассматривается
анолагичная задача на случай, когда представимые
числа принадлежат арифметической прогрессии по заданному модулю k.
Кроме того полечены достаточные условия для того, чтобы числа
некоторых арифметической прогрессии
представимые виде![]() ,
имели нулевую асимптотическую плотность.
,
имели нулевую асимптотическую плотность.
The problem about representation of natural numbers is considered at ought to the set class of deductions on some module and representable in a kind u+v where u and v members of two set sequences of natural mumbers. In 1934 N.P.Romanow has proved the theorem of positive density of sets of natural numbers representable in a kind p+am where r-runs simple numbers, m-natural numbers, and ≥2 the set integer. In the given work the similar problem on a case when representable numbers belong to an arithmetic progression on the set module to is considered. Besides sufficiens are treated that numbers of some arithmetic progressions representable in a kind p+am had zero asymptotic density.
Пусть
![]() - число натуральных чисел
- число натуральных чисел
![]() представимых в форме
представимых в форме
![]() и не превосходящих
и не превосходящих
![]() ,
,
где
![]() - показатель числа
- показатель числа
![]() по модулю
по модулю
![]() ,
,
с(k,l,a)-
плотность множеств натуральных чисел в
арифметических прогрессиях, представимых в виде
![]() .
.
После несложных рассуждений получаем
В связи с этим представляет интерес исследование вопроса о положительности суммы
Введём функцию
![]() (число решений сравнения
(число решений сравнения
![]() )
как известно, мультипликативна при
)
как известно, мультипликативна при
![]() (
(
![]() - простое число ) имеем:
- простое число ) имеем:
Поэтому
Отсюда видно, что если
![]() четно / поскольку мы предполагаем существование первообразного корня
по модулю
четно / поскольку мы предполагаем существование первообразного корня
по модулю
![]() ,
это означает, что
,
это означает, что
![]() ,
где
,
где
![]() - нечетное простое число,
- нечетное простое число,
![]() - целое /, а
- целое /, а
![]() - нечетно, то
- нечетно, то
![]() Таким образом справедлива.
Таким образом справедлива.
Теорема. Если
![]() ,
где
,
где
![]() - нечетное простое число,
- нечетное простое число,
![]() - целое, то во всех классах вычетов, порожденных нечетными числами,
множество чисел вида
- целое, то во всех классах вычетов, порожденных нечетными числами,
множество чисел вида
![]() ,
где
,
где
![]() - первообразный корень по
- первообразный корень по
![]() имеет нулевую асимптотическую плотность; во всех остальных классах
вычетов по
имеет нулевую асимптотическую плотность; во всех остальных классах
вычетов по
![]() плотность чисел вида
плотность чисел вида
![]() положительно.
положительно.
Литература:
- Romanov N.P. Uber einige Sartze der additiven Zahlentheorie, Math. Ann.109 (1934).668-678.
- Selberg S. A generalization of a theorem of Romanoff, Kong. Norse vid.Selsc. For handl. 35, 17 (1962), с.91-95
Фaйнлейб А.С., Оразов М. Бинарные аддитивные задачи с показательной функцией. Литовский математический сборник. 1978.№4. с.187-198.
Похожие статьи
число, арифметическая прогрессия, нечетное простое число...
Условия нулевой плотности множеств натуральных чисел... число, арифметическая прогрессия, нечетное простое число, нулевая асимптотическая плотность, первообразный корень.
Методы извлечения квадратного корня
Извлечение корня путем разложения подкоренного числа на простые множители.
где х-число, из которого надо извлечь корень, с-число ближайшего квадрата), например
Некоторые свойства арифметико-геометрической прогрессии
К таким последовательностям относятся арифметическая и геометрическая прогрессии, последовательность Фибоначчи и др. [1]. В данной статье представлены итоги исследования рекуррентной последовательности , заданной по правилу , где числа и называем...
Показательно-геометрическая прогрессия и некоторые ее свойства
Как известно, числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с некоторым числом, называется арифметической прогрессией.
Об использовании метода инварианта, основанного на идее...
Решения задач-головоломок с использованием четности и нечетности чисел отличаются логической безупречностью и абсолютной обоснованностью выводов, которые требуют знаний простейших свойств арифметических операций сложения и вычитания.
Исследование алгоритмов генерации простых чисел
Можно последовательно перебирать простые числа меньше заданного числа (точнее меньше ), чтобы найти все его делители. Тогда приобретает актуальность не столько время работы алгоритма, как его асимптотическое поведение при росте количества цифр числа .
Характеристическое свойство показательной прогрессии или...
Арифметическая прогрессия — это последовательность чисел, в которой каждое следующее число, начиная со второго, получается прибавлением к предыдущему постоянного числа.
Теорема Карамата и её применение в аддитивных задачах
Пусть U u V две последовательности натуральных чисел, и их подсчитывающие функции.
Таким образом, если , то справедливость асимптотической формулы (6) обеспечивается уже просто редкостью последовательности V. Арифметическая природа членов этой...
Непрерывные аналоги закона распределения простых чисел
Ингам А.Е. Распределение простых чисел.−
Таким образом, если , то справедливость асимптотической формулы (6) обеспечивается уже просто редкостью последовательности V. Арифметическая природа членов этой последовательности...
Похожие статьи
число, арифметическая прогрессия, нечетное простое число...
Условия нулевой плотности множеств натуральных чисел... число, арифметическая прогрессия, нечетное простое число, нулевая асимптотическая плотность, первообразный корень.
Методы извлечения квадратного корня
Извлечение корня путем разложения подкоренного числа на простые множители.
где х-число, из которого надо извлечь корень, с-число ближайшего квадрата), например
Некоторые свойства арифметико-геометрической прогрессии
К таким последовательностям относятся арифметическая и геометрическая прогрессии, последовательность Фибоначчи и др. [1]. В данной статье представлены итоги исследования рекуррентной последовательности , заданной по правилу , где числа и называем...
Показательно-геометрическая прогрессия и некоторые ее свойства
Как известно, числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с некоторым числом, называется арифметической прогрессией.
Об использовании метода инварианта, основанного на идее...
Решения задач-головоломок с использованием четности и нечетности чисел отличаются логической безупречностью и абсолютной обоснованностью выводов, которые требуют знаний простейших свойств арифметических операций сложения и вычитания.
Исследование алгоритмов генерации простых чисел
Можно последовательно перебирать простые числа меньше заданного числа (точнее меньше ), чтобы найти все его делители. Тогда приобретает актуальность не столько время работы алгоритма, как его асимптотическое поведение при росте количества цифр числа .
Характеристическое свойство показательной прогрессии или...
Арифметическая прогрессия — это последовательность чисел, в которой каждое следующее число, начиная со второго, получается прибавлением к предыдущему постоянного числа.
Теорема Карамата и её применение в аддитивных задачах
Пусть U u V две последовательности натуральных чисел, и их подсчитывающие функции.
Таким образом, если , то справедливость асимптотической формулы (6) обеспечивается уже просто редкостью последовательности V. Арифметическая природа членов этой...
Непрерывные аналоги закона распределения простых чисел
Ингам А.Е. Распределение простых чисел.−
Таким образом, если , то справедливость асимптотической формулы (6) обеспечивается уже просто редкостью последовательности V. Арифметическая природа членов этой последовательности...