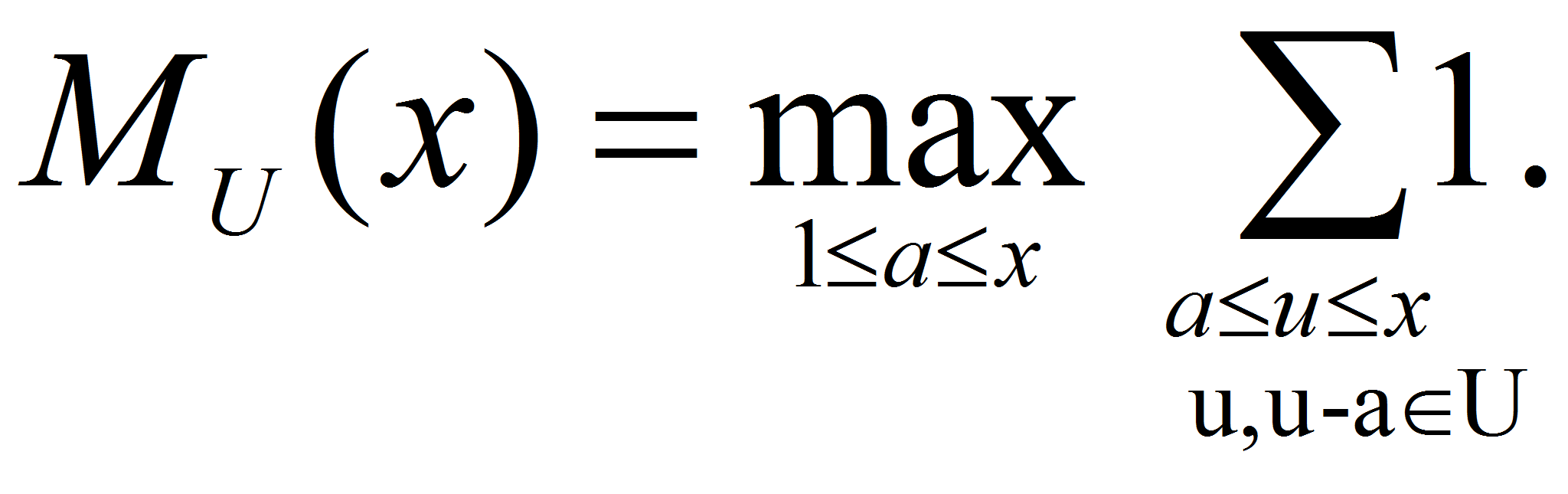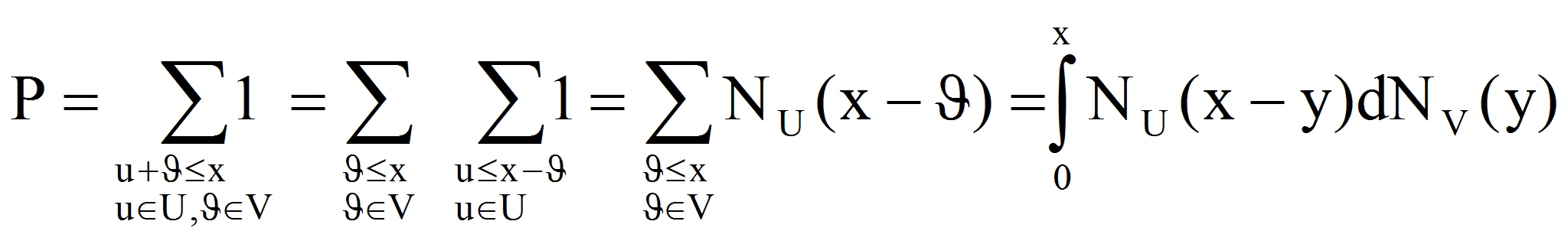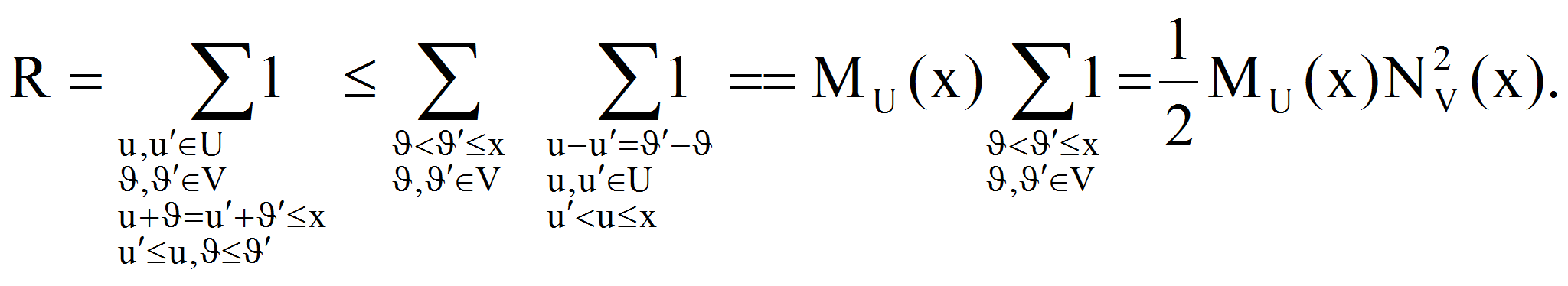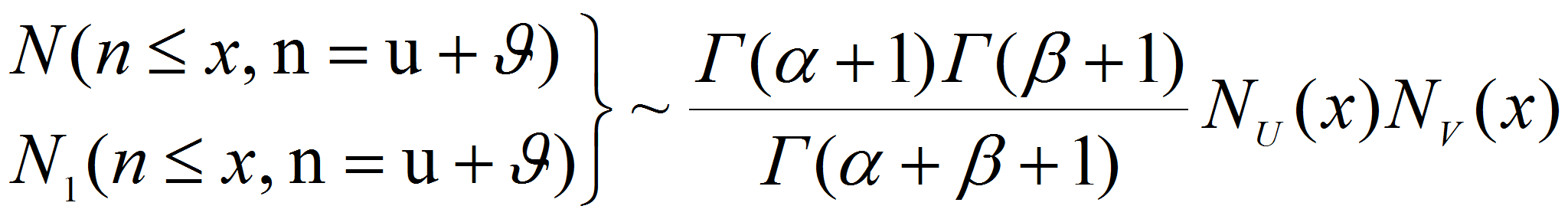Теорема Карамата и её применение в аддитивных задачах
Автор: Оразов Мамед
Рубрика: 14. Общие вопросы технических наук
Опубликовано в
международная научная конференция «Современные тенденции технических наук» (Уфа, октябрь 2011)
Статья просмотрена: 373 раза
Библиографическое описание:
Оразов, Мамед. Теорема Карамата и её применение в аддитивных задачах / Мамед Оразов. — Текст : непосредственный // Современные тенденции технических наук : материалы I Междунар. науч. конф. (г. Уфа, октябрь 2011 г.). — Уфа : Лето, 2011. — С. 68-70. — URL: https://moluch.ru/conf/tech/archive/5/952/ (дата обращения: 19.04.2024).
Пусть U u
V две последовательности
натуральных чисел,
![]() и
и
![]() их подсчитывающие функции. Введем обозначение
их подсчитывающие функции. Введем обозначение
Доказывается, что при наличии достаточно хорошей оценки MU(x) асимптотическая плотность суммы последовательностей U u V определяется асимптотикой свертки.
Let the u and v are two sequences of natural numbers, where Nu (x) and Nv (x) are their calculating functions. Let us introduce the notation
It is proved that while presence of sufficient positive estimate Mu (x) the asymptotic density of the sum of sequences of u and v is defined by asymptotic compression
Теорема. (Карамата [2]). Пусть f(t)
&#;неубывающая функция,
определенная для всех t &#;
0, f(0) = 0,
![]() ,
причем интеграл сходится при s >
0. Тогда, если по крайней мере одна из функций f(t)
или
,
причем интеграл сходится при s >
0. Тогда, если по крайней мере одна из функций f(t)
или
![]() &#; правильно меняющаяся функция
порядка &#; (в смысле
Карамата), то при
&#; правильно меняющаяся функция
порядка &#; (в смысле
Карамата), то при
![]()
Лемма 1. Пусть f(t)
и g(t)
&#; неубывающие
правильно меняющиеся функции порядков соответственно &#;
и &#;. Тогда при
![]()
Доказательство. Положим
![]() ;
функция h(t) неубывающая, так как
;
функция h(t) неубывающая, так как
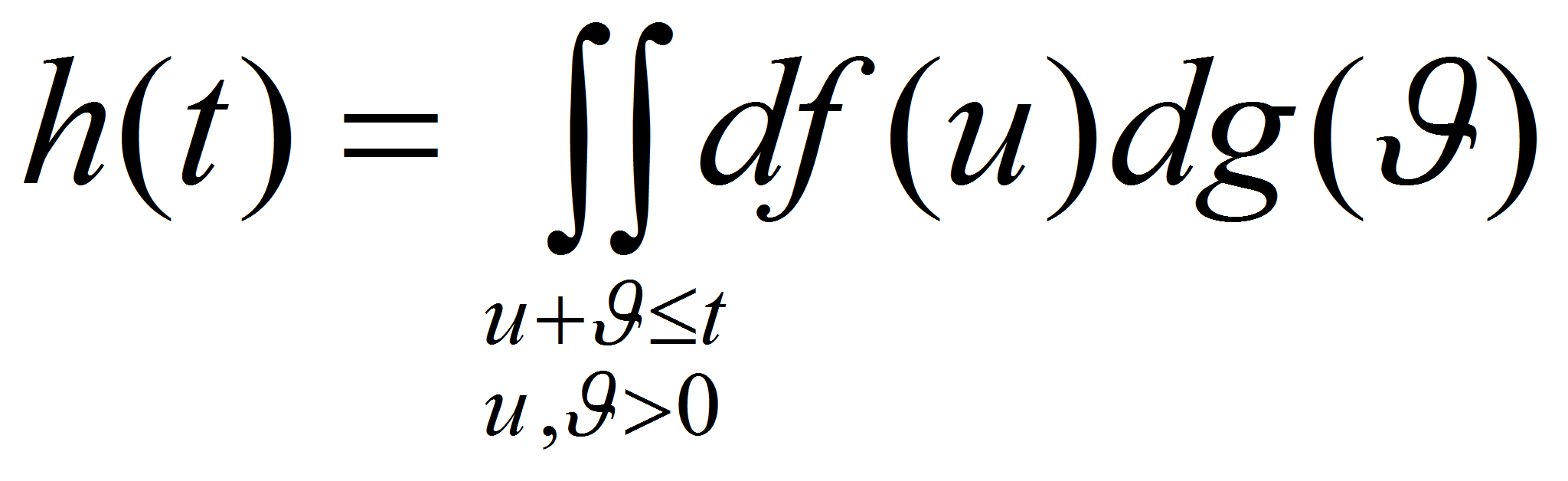 и
и
![]() .
.
Согласно теореме Карамата [2], при
![]()
откуда следует, что
![]() &#;
правильно меняющаяся функция порядка &#;+&#;.
Вторично применяя теорему Карамата [2], получаем
&#;
правильно меняющаяся функция порядка &#;+&#;.
Вторично применяя теорему Карамата [2], получаем
Пусть U и
V две возрастающие
последовательности натуральных чисел,
![]() и
и
![]() &#;
их подсчитывающие функции. Введем обозначение
&#;
их подсчитывающие функции. Введем обозначение
Теорема 1. Имеют место соотношения:
Доказательство. Применим неравенство
Романова-Эрдеша к множеству целых точек (u,&#;),
где
![]() .
Тогда
.
Тогда
- Заменяя P ,R полученными для них выражениями, получаем формулы (1), (2).
Теорема 1. показывает, что при наличии достаточно хорошей оценки
MU(x)
асимптотическая плотность суммы последовательностей U
и V
определяется асимптотикой свертки
![]()
Большинство последовательностей, рассматриваемых в аддитивной теории чисел, обладает правильно меняющимися подсчитывающими функциями. В этой ситуации из теоремы 1. следует
Теорема.2. Если
![]() и
и
![]() &#;
правильно меняющиеся функции порядков соответственно &#;
и &#;, причем
&#;
правильно меняющиеся функции порядков соответственно &#;
и &#;, причем
Доказательство. По лемме 1. в условиях теоремы 2.
Из условия (5) вытекает
Подставляя (7) и (8) в (1) и (2), получаем утверждение теоремы.
Таким образом, если
![]() ,
то справедливость асимптотической формулы (6) обеспечивается уже
просто редкостью последовательности V.
Арифметическая природа членов этой последовательности не играет
никакой роли.
,
то справедливость асимптотической формулы (6) обеспечивается уже
просто редкостью последовательности V.
Арифметическая природа членов этой последовательности не играет
никакой роли.
-
- Литература:
Шнирельман Л.Г. Об аддитивных свойствах чисел.&#; Изв. Донского политехнического института,1 ч, 1930, 3&#;28.
Karamata J. Journal für die reine und angewandt the Mathem. 104 (1931), 27&#;40
Барбан М.Б. Метод &#;большего решета&#; и его применения в теории чисел.&#; УМН, 21, 1(1966), 51&#;102
Левин Б.В., Файнлейб А.С. Применение некоторых интегральных уравнений к вопросам теории чисел.&#; УМН 22, №3 (35), 1967, 119&#;128.
Похожие статьи
Сильные средние уклонений операторов Валле Пуссена
функция, теорема, меняющаяся функция порядков, асимптотика свертки, меняющаяся функция порядка, хорошая оценка, асимптотическая плотность суммы...
О некоторых бинарных задачах для прогрессий | Статья в журнале...
Доказывается, что при наличии достаточно хорошей оценки MU(x) асимптотическая плотность суммы последовательностей U u V определяется асимптотикой свертки. Об использовании метода инварианта, основанного на идее...
Неравномерные оценки скорости сходимости в центральной...
Множество S образует алгебру относительно операций точечного умножения, сложения функций и поточечного умножения на скаляр.
Сначала рассмотрим непараметрическую оценку плотности вероятности по наблюдениям и изучим асимптотические свойства этой...
Непрерывные аналоги закона распределения простых чисел
Основные термины (генерируются автоматически): функция, неубывающая функция, прямая, теорема, асимптотическая формула.
Наилучшее приближение функции множеством определяется по формуле. Теорема 1 ([2]). Пусть , и , . Тогда для функции справедлива оценка.
Методика определения функций принадлежности для...
При существенно меньшем количестве функций принадлежности и правил в базе знаний, предложенная система на порядок превосходит описанные по
3. Горбань, А. Н. Обобщенная аппроксимационная теорема и вычислительные возможности нейронных сетей / А. Н. Горбань...
Метод последовательных приближений для системы уравнений...
удовлетворяющего оценке (11), где каратеодорева функция совпадает с на множестве.
Похожие статьи. Об асимптотическом поведении решений систем нелинейных...
Решение системы нелинейных дифференциальных уравнений высших порядков.
Об одной асимптотической оптимальной кубатурной формуле
Обобщённая функция. (2). называется функционалом погрешности кубатурной формулы (1)
Бахвалов Н. С. С Оценки снизу асимптотических характеристик классов функций с
Похожие статьи. Об одной весовой оптимальной по порядку сходимости кубатурной...
Асимптотика решения бисингулярной задачи на бесконечной...
Асимптотика решения построена обобщенным методом пограничных функций.
Последовательно применяя теорему 2 для уравнений (8) и (9), получаем.
Благодаря данному методу нам удалось получить точную оценку для остаточной функции.
Об асимптотическом поведении решений систем нелинейных...
уравнение, неизвестная функция, система, вектор, точное решение системы, условие теоремы, Теорема, матрица, вид, частное решение системы.
, . (2.4). Если ввести матрицу порядка и N-компонентные векторы и , то система примет матричный вид.
Похожие статьи
Сильные средние уклонений операторов Валле Пуссена
функция, теорема, меняющаяся функция порядков, асимптотика свертки, меняющаяся функция порядка, хорошая оценка, асимптотическая плотность суммы...
О некоторых бинарных задачах для прогрессий | Статья в журнале...
Доказывается, что при наличии достаточно хорошей оценки MU(x) асимптотическая плотность суммы последовательностей U u V определяется асимптотикой свертки. Об использовании метода инварианта, основанного на идее...
Неравномерные оценки скорости сходимости в центральной...
Множество S образует алгебру относительно операций точечного умножения, сложения функций и поточечного умножения на скаляр.
Сначала рассмотрим непараметрическую оценку плотности вероятности по наблюдениям и изучим асимптотические свойства этой...
Непрерывные аналоги закона распределения простых чисел
Основные термины (генерируются автоматически): функция, неубывающая функция, прямая, теорема, асимптотическая формула.
Наилучшее приближение функции множеством определяется по формуле. Теорема 1 ([2]). Пусть , и , . Тогда для функции справедлива оценка.
Методика определения функций принадлежности для...
При существенно меньшем количестве функций принадлежности и правил в базе знаний, предложенная система на порядок превосходит описанные по
3. Горбань, А. Н. Обобщенная аппроксимационная теорема и вычислительные возможности нейронных сетей / А. Н. Горбань...
Метод последовательных приближений для системы уравнений...
удовлетворяющего оценке (11), где каратеодорева функция совпадает с на множестве.
Похожие статьи. Об асимптотическом поведении решений систем нелинейных...
Решение системы нелинейных дифференциальных уравнений высших порядков.
Об одной асимптотической оптимальной кубатурной формуле
Обобщённая функция. (2). называется функционалом погрешности кубатурной формулы (1)
Бахвалов Н. С. С Оценки снизу асимптотических характеристик классов функций с
Похожие статьи. Об одной весовой оптимальной по порядку сходимости кубатурной...
Асимптотика решения бисингулярной задачи на бесконечной...
Асимптотика решения построена обобщенным методом пограничных функций.
Последовательно применяя теорему 2 для уравнений (8) и (9), получаем.
Благодаря данному методу нам удалось получить точную оценку для остаточной функции.
Об асимптотическом поведении решений систем нелинейных...
уравнение, неизвестная функция, система, вектор, точное решение системы, условие теоремы, Теорема, матрица, вид, частное решение системы.
, . (2.4). Если ввести матрицу порядка и N-компонентные векторы и , то система примет матричный вид.