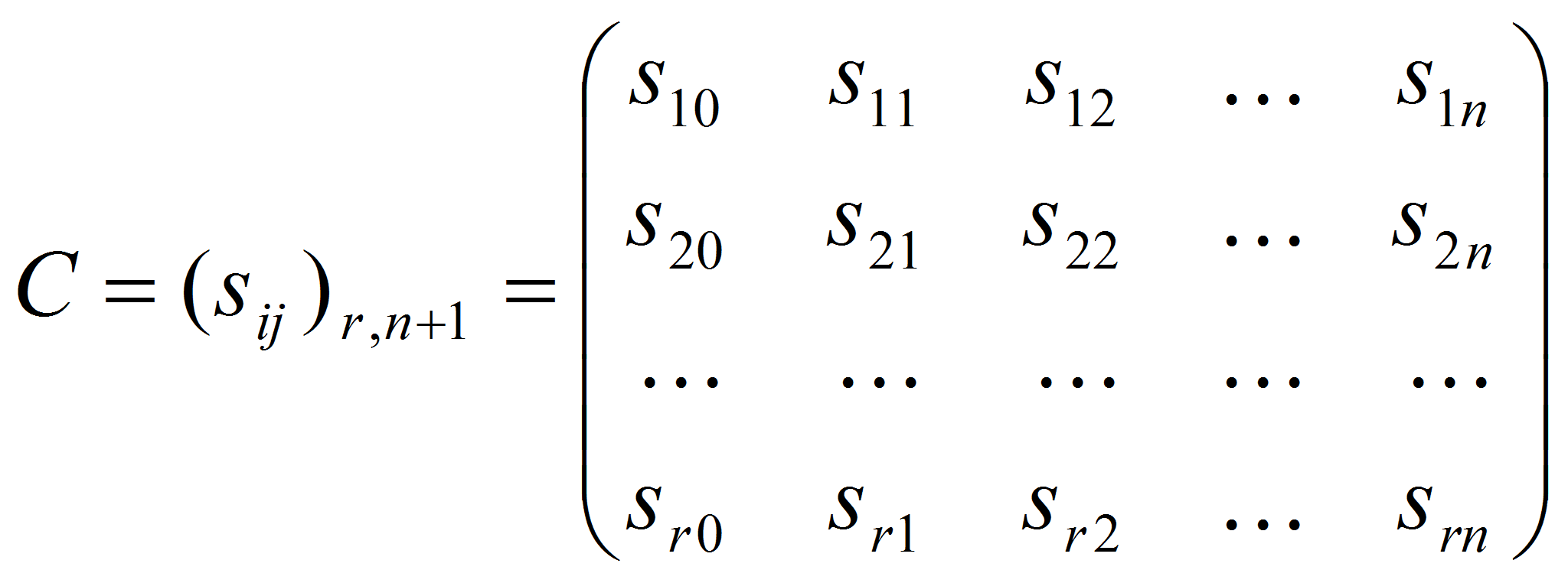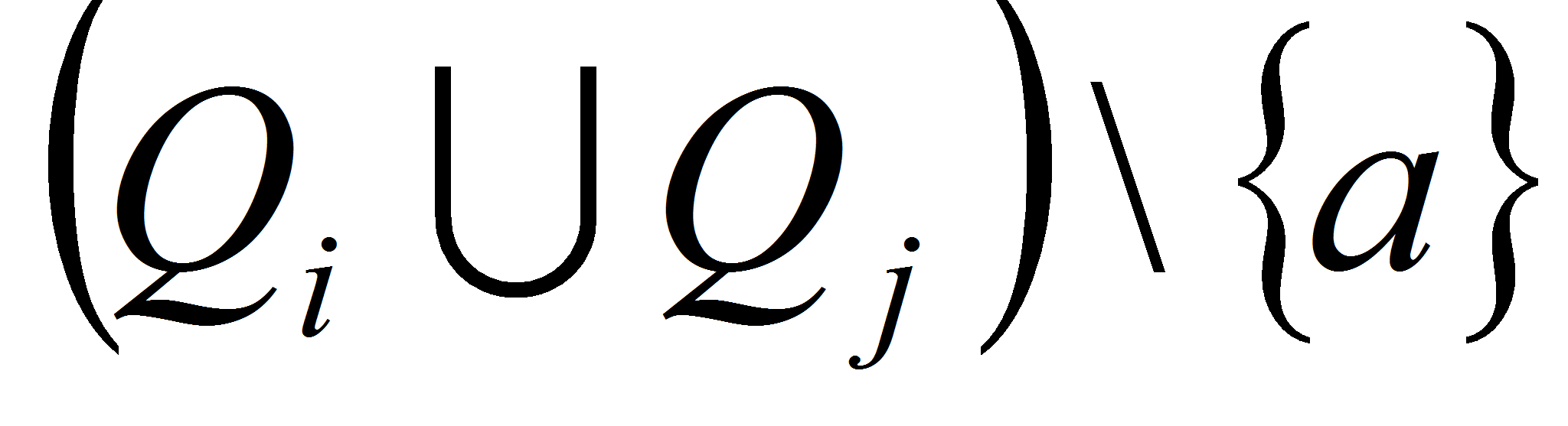Методы пространственного разделения секретной информации образуют одну из основ систем активной безопасности распределённых компьютерных систем. Среди таких методов широко применяются криптографические схемы разделения секрета. Необходимо пояснить, что данные схемы позволяют разделить секрет между некоторым количеством участников обмена информацией, соблюдая следующие условия [2, 3]:
- Заранее заданные разрешенные множества участников, образующие структуру доступа, могут однозначно восстановить секрет.
- Участники, образующие неразрешенные множества, не могут получить никакой дополнительной к имеющейся априорной информации о возможном значении секрета.
Пусть в информационном взаимодействии участвуют
![]() абонентов. Обозначим множество всех абонентов через
абонентов. Обозначим множество всех абонентов через
![]() ,
где
,
где
![]() .
Далее обозначим
.
Далее обозначим
![]() -
как некоторое подмножество множества
-
как некоторое подмножество множества
![]() ,
имеем
,
имеем
![]() .
Множество
.
Множество
![]() входят все разрешенные множества абонентов схемы, которые могут
восстановить секретную информацию после процесса пространственного
разделения. Если
входят все разрешенные множества абонентов схемы, которые могут
восстановить секретную информацию после процесса пространственного
разделения. Если
![]() ,
то
,
то
![]() есть разрешенное множество, иначе
есть разрешенное множество, иначе
![]() есть
неразрешенное множество. Все участники схемы относительно структуры
доступа
есть
неразрешенное множество. Все участники схемы относительно структуры
доступа
![]() делятся
на две группы: существенные и несущественные.
делятся
на две группы: существенные и несущественные.
Участники схемы
![]() ,
где
,
где
![]() ,
будем считать несущественные относительно
,
будем считать несущественные относительно
![]() ,
если для любого неразрешенного множества
,
если для любого неразрешенного множества
![]() множество
множество
![]() также является неразрешенным. Следовательно, элемент
также является неразрешенным. Следовательно, элемент
![]() существенен
относительно структуры доступа
существенен
относительно структуры доступа
![]() ,
при условии существования множества
,
при условии существования множества
![]() ,
,
![]() ;
;
![]() .
.
Зададим множества
![]() и совместное распределение вероятностей
и совместное распределение вероятностей
![]() на их декартовом произведении
на их декартовом произведении
![]() .
Соответствующие случайные величины обозначаются следующим образом
.
Соответствующие случайные величины обозначаются следующим образом
![]() .
.
![]() -
это множество всех возможных секретов. Значение секрета
-
это множество всех возможных секретов. Значение секрета
![]() выбирается
с вероятностью
выбирается
с вероятностью
![]() и
с помощью схемы разделения секрета распределяется в виде
и
с помощью схемы разделения секрета распределяется в виде
![]() между
всеми абонентами схемы с вероятностью
между
всеми абонентами схемы с вероятностью
![]() .
При этом схема строится следующим образом. Каждый i
-й участник получает соответствующую долю секрета
.
При этом схема строится следующим образом. Каждый i
-й участник получает соответствующую долю секрета
![]() ,
знает все множества
,
знает все множества
![]() ,
распределения вероятностей
,
распределения вероятностей
![]() и
и
![]() ,
но не имеет никакой информации о проекциях секрета, которые получили
другие участники схемы. Так же распределение вероятностей
,
но не имеет никакой информации о проекциях секрета, которые получили
другие участники схемы. Так же распределение вероятностей
![]() и
и
![]() можно заменить на
можно заменить на
Рассмотрим схему разделения секрета с точки зрения теории вероятностей [1, 3].
Определение 1. Пара
![]() совершенной вероятностной схемой разделения секрета, реализующей
структуру доступа
совершенной вероятностной схемой разделения секрета, реализующей
структуру доступа
![]() ,
если выполнены следующие условия:
,
если выполнены следующие условия:
Далее введем понятие энтропии дискретной случайной
величины [4, 7, 9]. Под энтропией будем понимать меру степени
неопределенности дискретной случайной величины. Если
![]() -
дискретная величина, принимающая значения
-
дискретная величина, принимающая значения
![]() с распределением вероятностей
с распределением вероятностей
![]() ,
где
,
где
![]() ,
то энтропия определяется формулой
,
то энтропия определяется формулой
- Модифицируем условия 1 и 2 из определения 1 с учетом понятия энтропии:
Также вероятностное определение совершенной схемы разделения секрета может быть переведено на комбинаторный язык.
Существует матрица
Элементы данной матрицы составляют комбинаторную схему разделения
секрета, а строки формируют «правила» распределения
секрета. Матрицу
![]() будем называть кодом комбинаторной схемы разделения секрета, а ее
строки – словами. При выборе правила распределения секрета для
заданного значения
будем называть кодом комбинаторной схемы разделения секрета, а ее
строки – словами. При выборе правила распределения секрета для
заданного значения
![]() необходимо
случайно и равномерно выбрать строку
необходимо
случайно и равномерно выбрать строку
![]() из тех строк матрицы
из тех строк матрицы
![]() ,
для которых значение нулевой координаты равно
,
для которых значение нулевой координаты равно
![]() ,
т.е.
,
т.е.
![]() и
и
![]() .
В комбинаторной модели необходимо:
.
В комбинаторной модели необходимо:
-
для любого множества
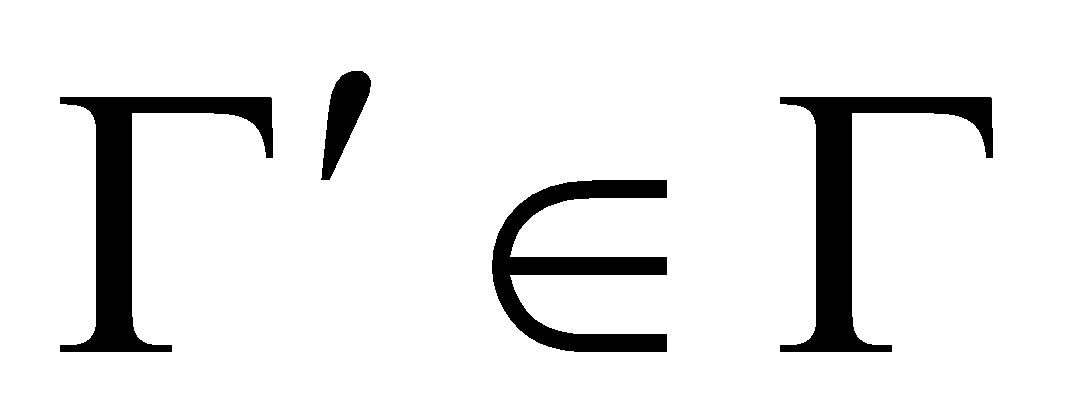 нулевая координата любого кодового слова из
нулевая координата любого кодового слова из
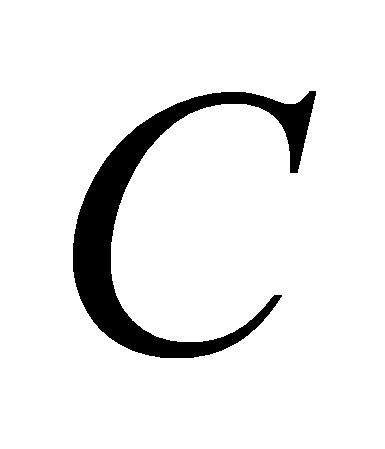 однозначно
определялась значениями его координат из множества
однозначно
определялась значениями его координат из множества
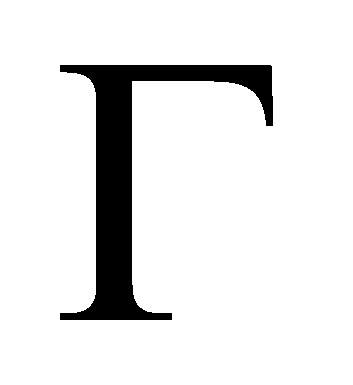 ;
; -
для любого множества
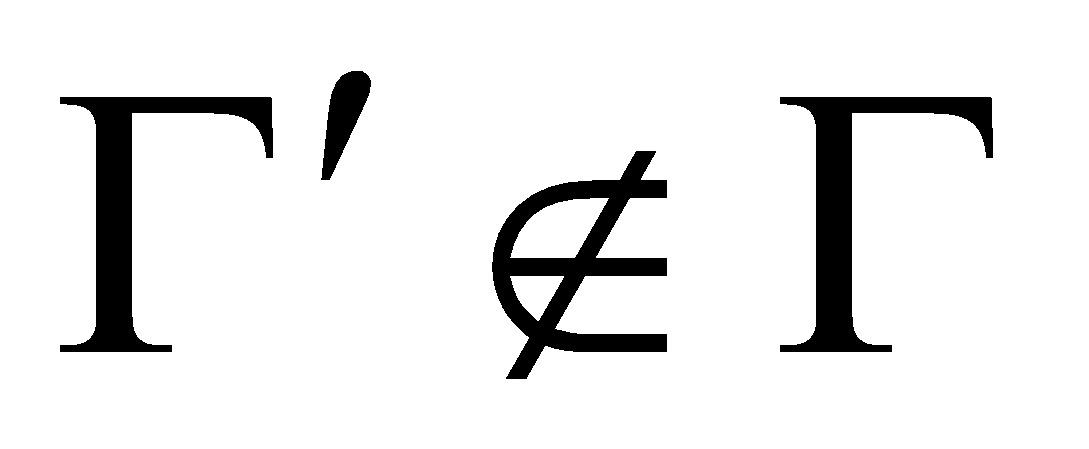 и любых заданных значений координат из множества
и любых заданных значений координат из множества
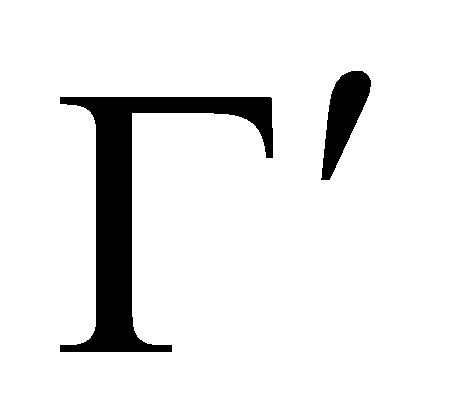 .
.
Исходя из вышесказанного, можно дать определение совершенной комбинаторной схемы разделения секрета:
Определение 2. Матрица
![]() задает совершенную комбинаторную схему разделения секрета,
реализующую структуру доступа
задает совершенную комбинаторную схему разделения секрета,
реализующую структуру доступа
![]() ,
если выполняются следующие условия:
,
если выполняются следующие условия:
-
Для любого множества
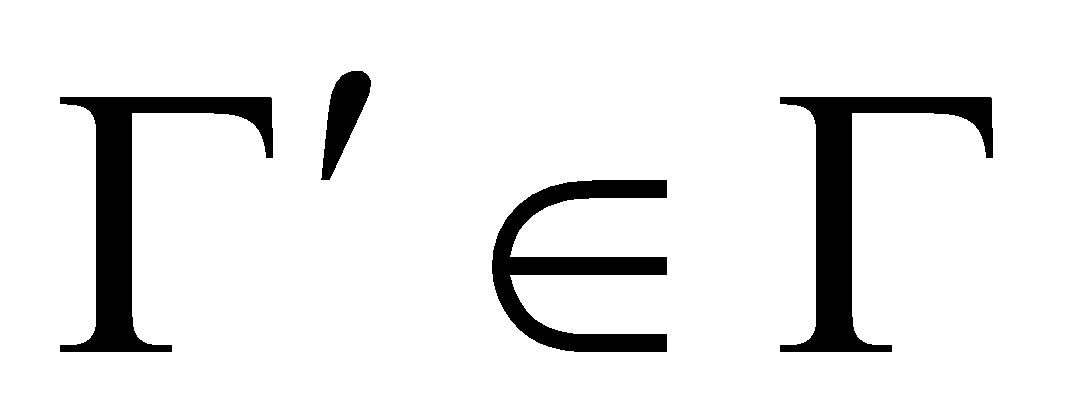 нулевая координата любой строки матрицы
нулевая координата любой строки матрицы
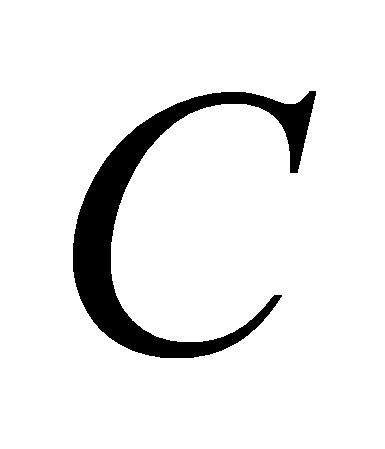 однозначно определяется значениями ее координат из множества
однозначно определяется значениями ее координат из множества
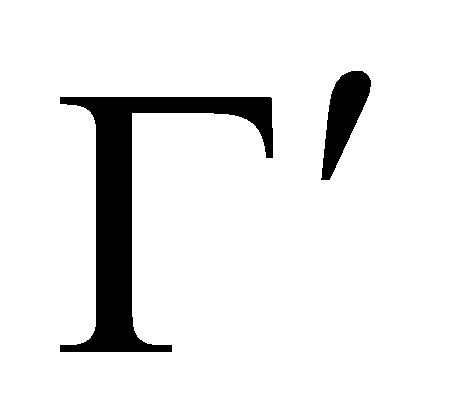 .
. -
Для любого множества
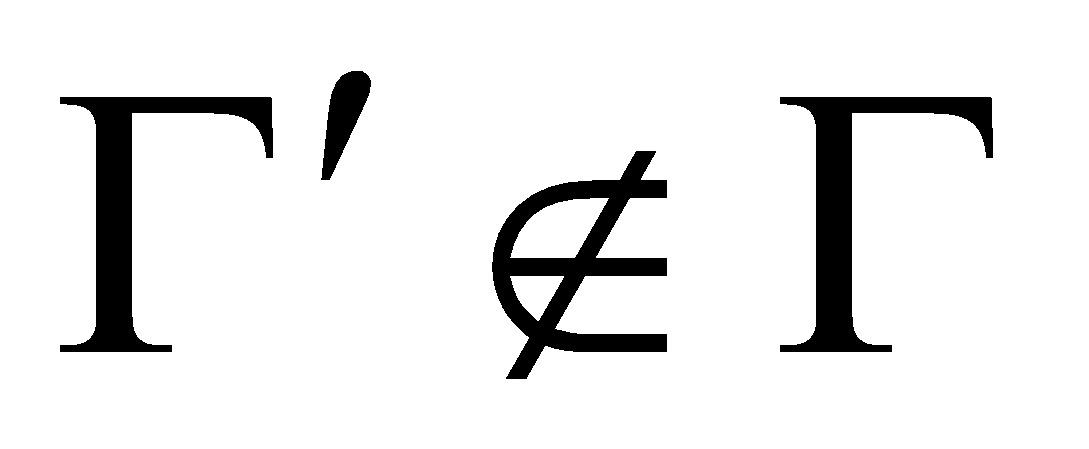 и любых заданных значений координат из множества
и любых заданных значений координат из множества
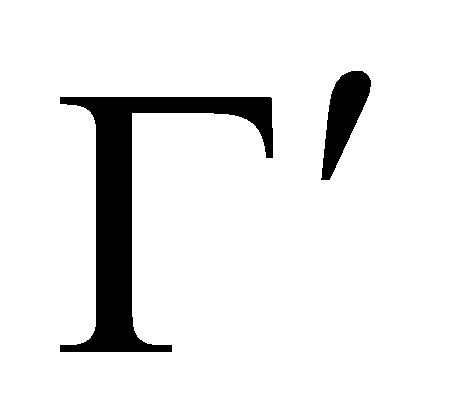 число строк матрицы
число строк матрицы
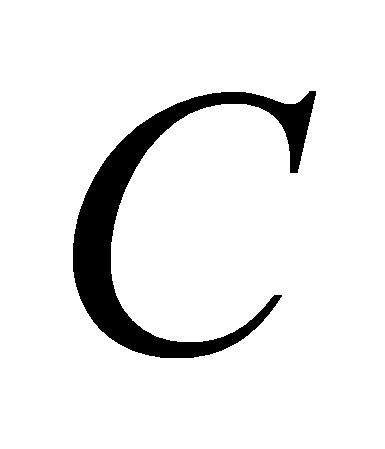 с данным значением
с данным значением
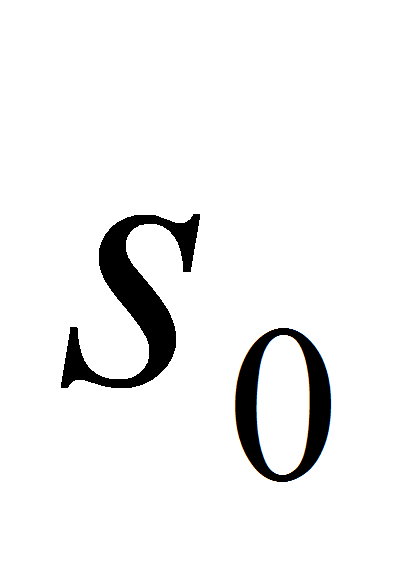 нулевой
координаты не зависит от
нулевой
координаты не зависит от
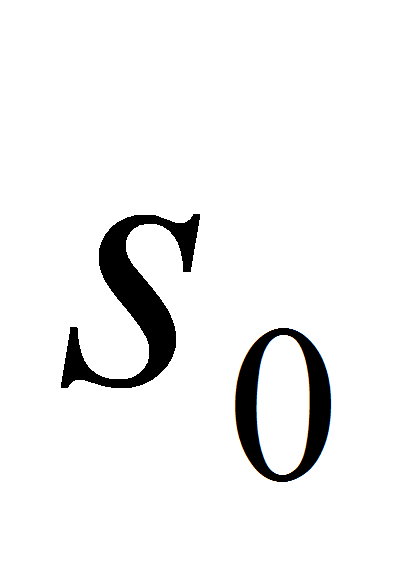 .
.
Необходимо отметить, что комбинаторная модель
является частным случаем вероятностной модели, когда все нулевые
значения
![]() одинаковы.
одинаковы.
Далее сформулируем более общее определение совершенной комбинаторной схемы разделения секрета [1].
За обозначение кода, полученного из
![]() удалением координат (номера которых не принадлежат множеству
удалением координат (номера которых не принадлежат множеству
![]() ,
где
,
где
![]() ),
примем
),
примем
![]() .
Пусть
.
Пусть
![]() обозначает число различных слов в коде
обозначает число различных слов в коде
![]() .
Для произвольной комбинаторной схемы, задаваемой кодом
.
Для произвольной комбинаторной схемы, задаваемой кодом
![]() ,
определим на множествах
,
определим на множествах
![]() функцию
функцию
![]() ,
где
,
где
![]() .
.
Определение 3. Будем говорить, что код
![]() задает совершенную комбинаторную схему разделения секрета, если
задает совершенную комбинаторную схему разделения секрета, если
![]() ,
или, эквивалентно, если
,
или, эквивалентно, если
где
![]() определяется, так же как и в (1).
определяется, так же как и в (1).
Необходимо выделить ещё одну разновидность схем разделения секрета, а
именно так называемые идеальные схемы разделения секрета. Основной
характеристикой таких систем заключается в том, что объем секрета не
меньше отъема информации, предоставляемой участнику. Для любых
совершенной вероятностной схемы разделения секрета для всех
![]() справедливо неравенство [10, 11]
справедливо неравенство [10, 11]
Из неравенства (3) и из определения схемы разделения секрета следует,
что совершенная вероятностная схема называется идеальной, если
![]() для всех
для всех
![]() .
.
Структуры доступа
![]() ,
для которых существуют идеальные схемы разделения секрета, могут быть
описаны теорией матройдов. Матройд - классификация подмножеств
некоторого множества, представляющая собой обобщение идеи
независимости элементов, аналогично независимости элементов линейного
пространства, на произвольное множество.
,
для которых существуют идеальные схемы разделения секрета, могут быть
описаны теорией матройдов. Матройд - классификация подмножеств
некоторого множества, представляющая собой обобщение идеи
независимости элементов, аналогично независимости элементов линейного
пространства, на произвольное множество.
Иными словами Матройд есть конечное множество
![]() и семейство
и семейство
![]() подмножеств множества
подмножеств множества
![]() ,
называемых независимыми множествами, для которых возможно выполнение
аксиом [1, 3, 6]:
,
называемых независимыми множествами, для которых возможно выполнение
аксиом [1, 3, 6]:
-
Пустое множество независимо (
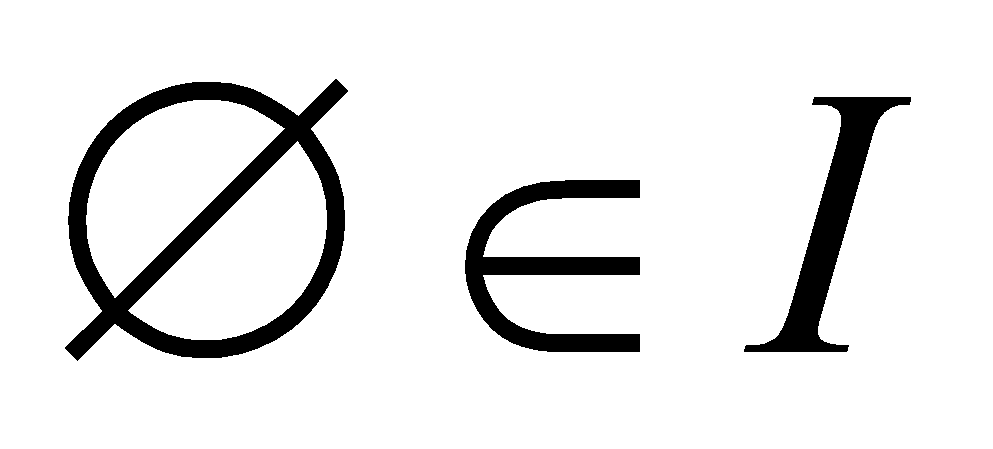 ).
). -
Каждое подмножество независимого множества независимо:
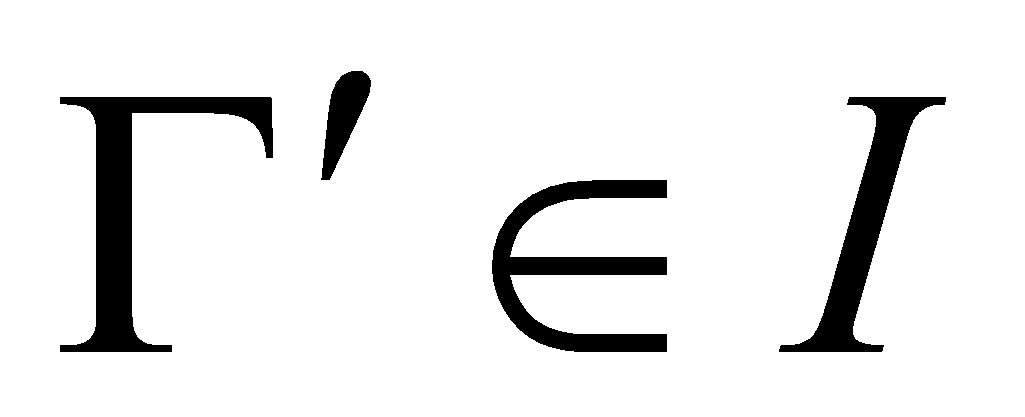 и
и
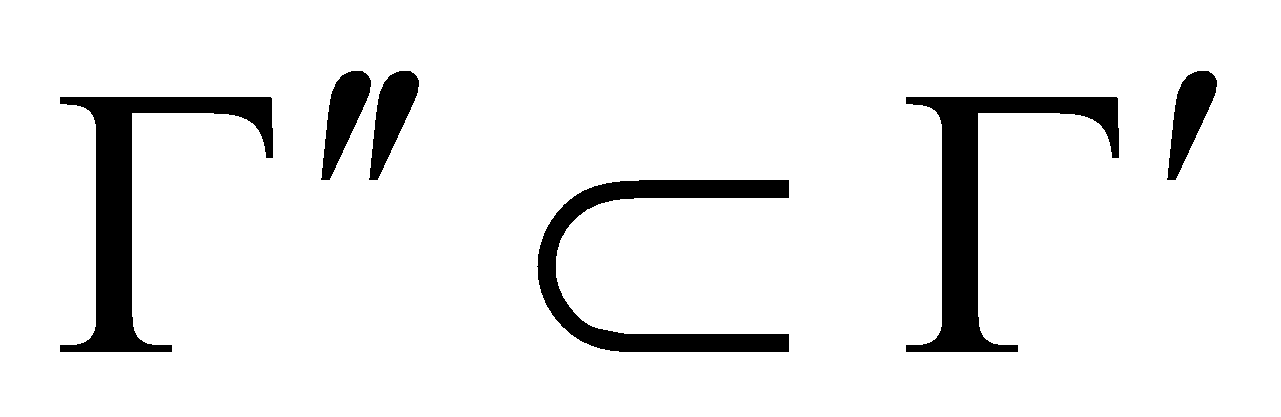 ,
то
,
то
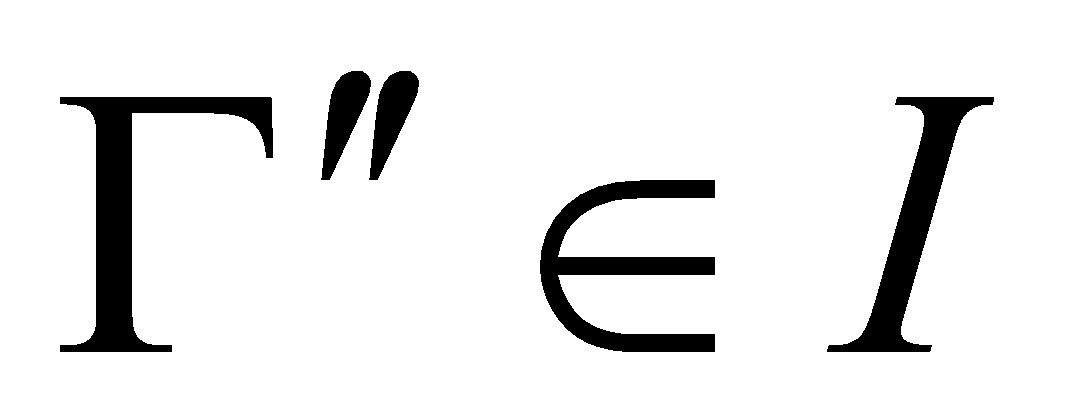 .
. -
Если
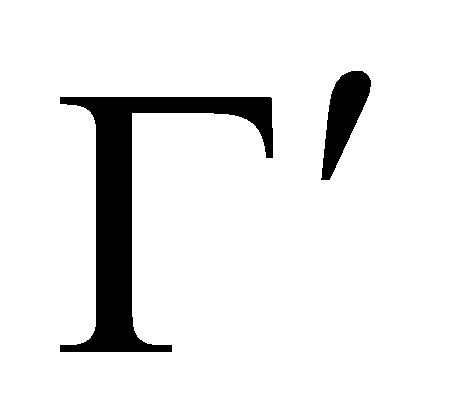 ,
,
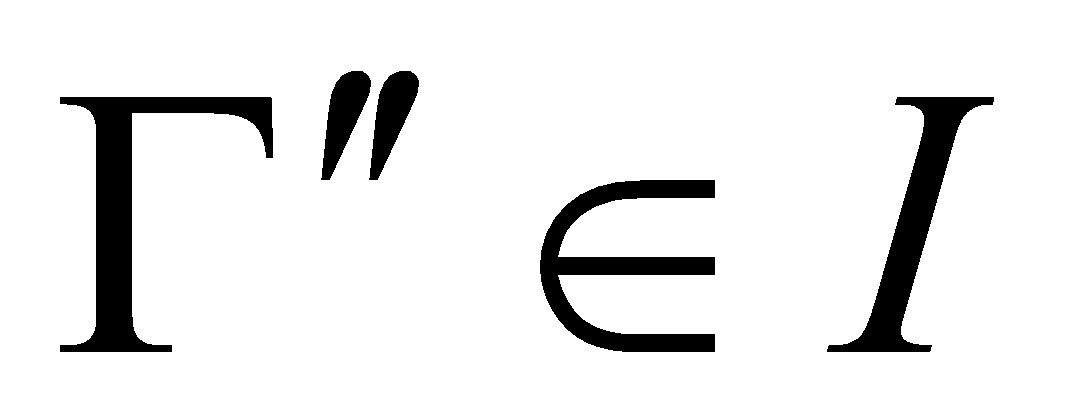 и
и
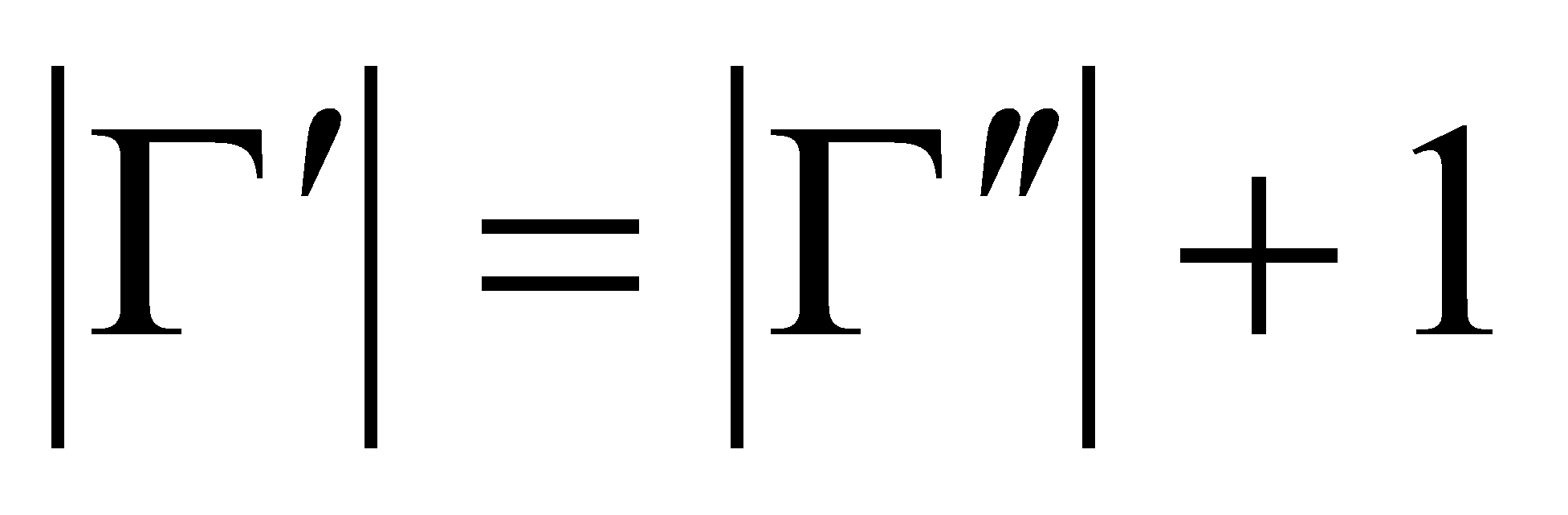 ,
то существует элемент
,
то существует элемент
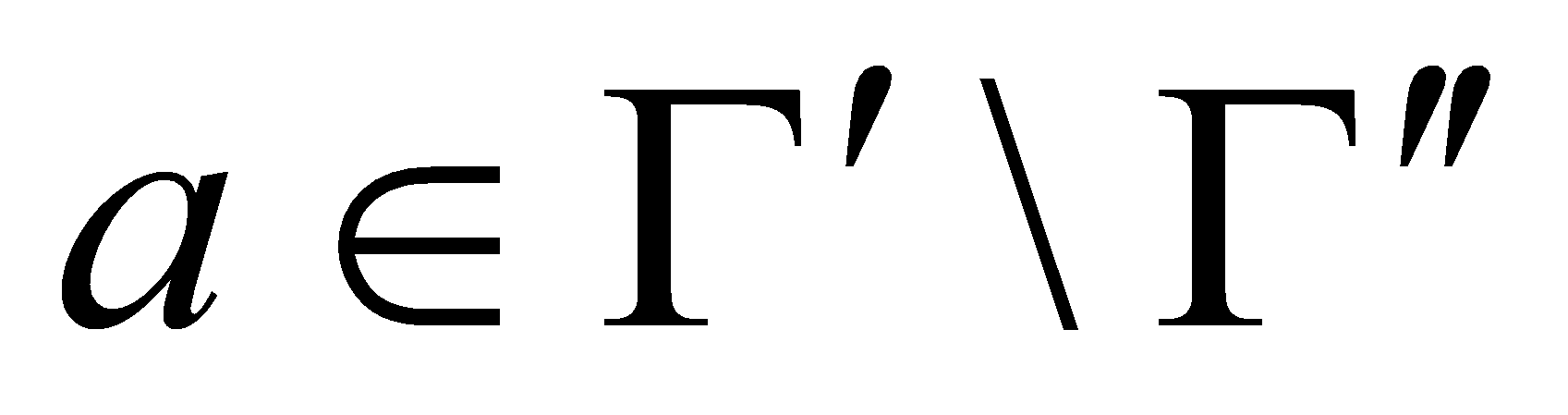 такой, что
такой, что
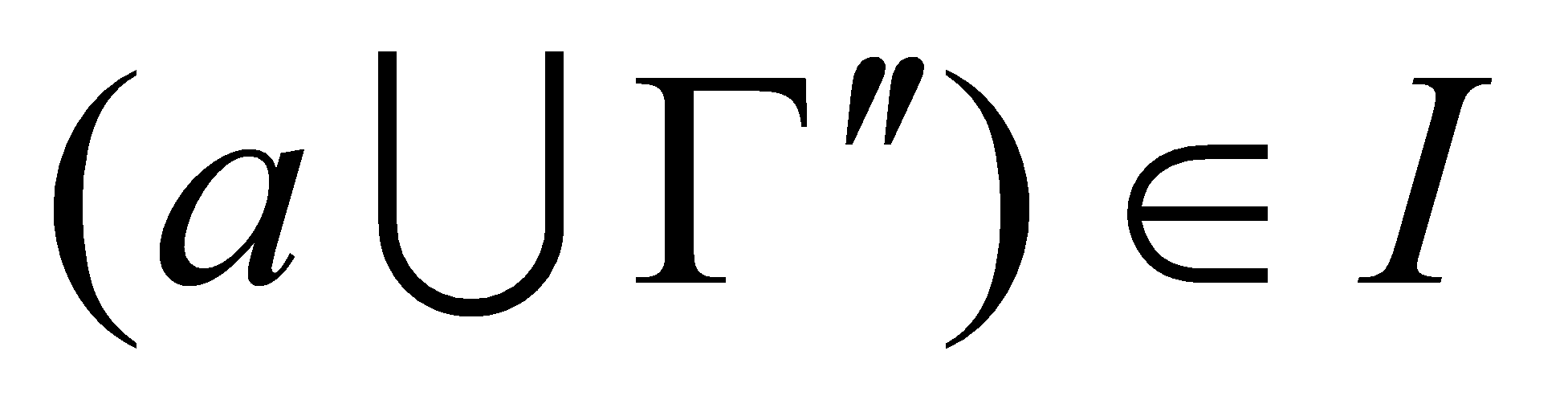 .
.
Матройд можно определить через так называемую
ранговую функцию
![]() матройда, определяемую как максимальная мощность независимого
подмножества
матройда, определяемую как максимальная мощность независимого
подмножества
![]() [3, 5]. Независимые условия задаются
условием
[3, 5]. Независимые условия задаются
условием
![]() .
Опишем свойства ранговой функции:
.
Опишем свойства ранговой функции:
Матройд можно задать конечным множеством элементов
![]() и семейством
и семейством
![]() ,
множества которого являются непустыми (
,
множества которого являются непустыми (![]() ),
называемых циклами. Для таких элементов существуют аксиомы [8]:
),
называемых циклами. Для таких элементов существуют аксиомы [8]:
Матройд называется связным, если для любых его двух точек существует содержащий их цикл.
Существует подход согласно которому, есть связь между матройдами и совершенными схемами разделения секрета [1].
Теорема 1. Для любой обобщенной идеальной
схемы разделения секрета
![]() ,
реализующей структуру доступа
,
реализующей структуру доступа
![]() ,
независимые множества
,
независимые множества
![]() ,
определяемые условием
,
определяемые условием
![]() ,
задают связный матройд на множестве
,
задают связный матройд на множестве
![]() .
Все циклы множества содержащие точку 0, имеют вид
.
Все циклы множества содержащие точку 0, имеют вид
![]() ,
где
,
где
![]() .
.
Из теоремы 1 следует, что между комбинаторными и вероятностными схемами разделения секрета существенной разницы нет.
Стоит учесть, что не любой матройд может быть реализован как идеальная схема разделения секрета, но при этом любой линейный матройд может быть реализован как идеальная схема разделения секрета.
В большинстве случаев для криптографической защиты секретных ключей чаще всего на практике используются пороговые криптосистемы. Данный подход обеспечивает устойчивость процесса обработки и сохранности ключевого материала в условиях неблагоприятных внешних воздействий.
- Литература:
- Блейкли Р.Г., Кабатянский Г.Р. Обобщение идеальные схемы, разделяющие секрет и матройды // Проблемы передачи информации. – 1997. – Т.33. - №3. – C. 42-46.
- Бугров Я.С., Никольский С.М. Высшая математика. Элементы линейной алгебры и аналитической геометрии: Учебник для вузов. – 4-е изд., перераб. и доп. – Ростов – на – Дону: Феникс, 1997. – 268 с.
- Введение в криптографию / Под общ. ред. В.В. Ященко. – М.: МЦНМО, «ЧеРо», 1998. – 272 с.
- Вентцель Е.С. Теория вероятностей: Учеб. для вузов. – 6-е изд. стер. – М.: Высш. шк., 1999. – 576 с.
- Иванов М.А. Криптографические методы защиты информации в компьютерных системах и сетях. – М.: КУДИЦ – ОБРАЗ, 2001. – 368 с.
- Математическая энциклопедия: В 5 т / под ред. И.М. Виноградова. – М.: Советская энциклопедия, 1982. – Т.3. – 1184 стб.
- Математическая энциклопедия: В 5 т / под ред. И.М. Виноградова. – М.: Советская энциклопедия, 1984. – Т.5. – 1248 стб.
- Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2001. – 304 с.
- Яглом А.М., Яглом И.М. Вероятность и информация. М.: Наука, 1973. – 512 с.
- Capocelli R.M., De Santis A., Cargano L., Vaccaro U. On the Size of Shares for Secret Sharing Schemes // J. Cryptology. – 1993. V.6 – P. 157-167.
- Carnin E.D., Greene J.W., Hellman M.E. On Secret Sharing Systems // IEEE Trans. Inform. Theory. – 1983. – V.29. - №1. – P.231-241.