Применение систем компьютерной алгебры для визуализации математических объектов и их преобразований на уроках математики
Авторы: Гуров Михаил Николаевич, Жмурова Ирина Юньевна
Рубрика: 5. Педагогика общеобразовательной школы
Опубликовано в
XI международная научная конференция «Актуальные задачи педагогики» (Краснодар, февраль 2020)
Дата публикации: 09.01.2020
Статья просмотрена: 897 раз
Библиографическое описание:
Гуров, М. Н. Применение систем компьютерной алгебры для визуализации математических объектов и их преобразований на уроках математики / М. Н. Гуров, И. Ю. Жмурова. — Текст : непосредственный // Актуальные задачи педагогики : материалы XI Междунар. науч. конф. (г. Краснодар, февраль 2020 г.). — Краснодар : Новация, 2020. — С. 22-26. — URL: https://moluch.ru/conf/ped/archive/358/15584/ (дата обращения: 26.04.2024).
В статье авторы рассматривают возможность применения современных средств динамической визуализации на уроках математики при когнитивно-визуальном подходе к обучению. Описывается опыт применения когнитивно-визуального подхода при изучении математики в общеобразовательной организации.
Ключевые слова: визуализация на уроках математики, когнитивно-визуальный подход, системы компьютерной алгебры, динамическая визуализация.
Математика — наука не столько для ушей, сколько для глаз.
Карл Фридрих Гаусс
Ни для кого не секрет, что в абсолютном большинстве случаев основной упор при обучении математике делается на развитие логического и аналитического мышления учащихся, то есть на развитие левого полушария головного мозга. При этом правое полушарие, отвечающее за наглядно-образное мышление, зачастую задействовано недостаточно. А поскольку современная психофизиология утверждает, что до 80 % информации человек получает посредством зрительного восприятия [5], то мы не должны упускать столь серьезный инструмент обучения математике как визуализация.
Методика преподавания математики — наука консервативная. Она четко регламентирует цели, содержание, методы, формы и средства обучения. Однако уже сегодня ведущие педагоги предлагают ослабить «строгие математические рамки» школьного образования (см., например, [2, c. 4] и [3, c. 223]). В частности, замечательный ученый и педагог А. Г. Мордкович призывает: «Меньше схоластики, меньше формализма, меньше жестких моделей, меньше опоры на левое полушарие мозга! Больше геометрических иллюстраций, больше наглядности, больше правдоподобных рассуждений, больше мягких моделей, больше опоры на правое полушарие мозга!» [2, с. 5]. И если раньше (15–20 лет назад) такого рода призывы могли показаться очень трудоемкими при организации учебного процесса, то сегодня технологии развились настолько, что создание визуальных образов математических объектов осуществляется в специальных программах за считанные секунды.
Такие программы можно условно разделить на два класса:
- Узкоспециализированные программные комплексы для решения определенных педагогических и математических задач. К ним относятся, например, desmos [6] (передовой графический калькулятор, реализованный как приложение для браузера и мобильное приложение), GeoGebra [7] (кросс-платформенная динамическая математическая программа для всех уровней образования, включающая в себя геометрию, алгебру, таблицы, графы, статистику и арифметику) и SMART Notebook [8] (программное обеспечение, позволяющее создавать интерактивные уроки, использовать большое количество готового контента).
- Системы компьютерной алгебры (СКА) — программы для выполнения преобразований и работы с математическими выражениями в аналитической (символьной) форме, а также с геометрическими объектами. К ним относятся, например, Wolfram Mathematica [9] (система компьютерной алгебры, широко используемая в научных, инженерных, математических и компьютерных областях), Mathcad [10] (система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вычислениями и визуальным сопровождением) и MATLAB [11] (высокоуровневый язык и интерактивная среда для программирования, численных расчетов и визуализации результатов. С помощью MATLAB можно анализировать данные, разрабатывать алгоритмы, создавать модели и приложения).
Стоит отметить, что любая из упомянутых программ может быть использована для создания графических образов математических объектов и визуализации их преобразований.
Проблема повышения эффективности обучения школьников на уроках математики путем реализации принципа наглядности неоднократно поднималась в отечественной педагогике. В частности, профессор В. А. Далингер высказывает следующую позицию: «Проблема реализации принципа наглядности в обучении математике может получить принципиально новое решение, если удастся найти такое методическое обеспечение деятельности ученика, которое позволит включить функции его визуального мышления для получения продуктивных результатов в овладении математическими понятиями, для усиления развивающей функции математики. Использование наглядных образов в обучении может превратиться из вспомогательного, иллюстрирующего приема в ведущее, продуктивное методическое средство, способствующее математическому развитию учащихся. Язык образов является основным средством наглядности при изучении математики, позволяющим осознано оперировать с понятиями и умозаключениями, закреплять и «оживлять» их в памяти» [1, с. 299]. Решение проблемы, озвученной профессором Далингером, как нам кажется, может быть найдено путем активного использования средств визуализации современных систем компьютерной алгебры на уроках математики.
На уроках алгебры, например, полезно давать графическую интерпретацию решения уравнений. Так, методологически решение уравнения ![]() намного удобней представить графически[1], нежели аналитически (Рис. 1), причем в абсолютном большинстве СКА это делается при помощи всего одной команды.
намного удобней представить графически[1], нежели аналитически (Рис. 1), причем в абсолютном большинстве СКА это делается при помощи всего одной команды.
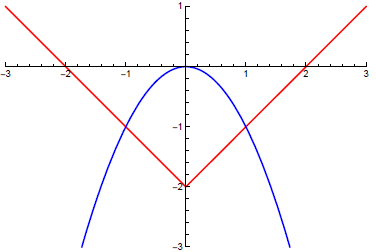
Рис. 1
При изучении квадратных уравнений ![]() на уроках алгебры с помощью средств визуализации СКА можно без труда объяснить геометрический смысл такой «непонятной» для многих обучающихся величины как дискриминант (
на уроках алгебры с помощью средств визуализации СКА можно без труда объяснить геометрический смысл такой «непонятной» для многих обучающихся величины как дискриминант (![]() ). Согласно определению дискриминантом будем называть такое число
). Согласно определению дискриминантом будем называть такое число ![]() , что расстояние от оси симметрии параболы
, что расстояние от оси симметрии параболы ![]() до ее нулей равно
до ее нулей равно ![]() (Рис. 2).
(Рис. 2).
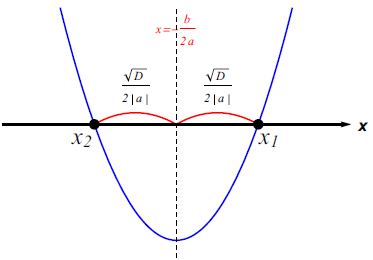
Рис. 2
Более того, такое графическое представление понятия «дискриминант» сразу решает вопрос о количестве действительных корней квадратного уравнения и дает четкое представление о корнях четной кратности, что является основой для решения неравенств (задача 15) на ЕГЭ по математике профильного уровня.
При изучении тригонометрии можно не только легко визуализировать, например, основное тригонометрическое тождество (Рис. 3), но и показать процесс построения графиков тригонометрических функций (Рис. 4).
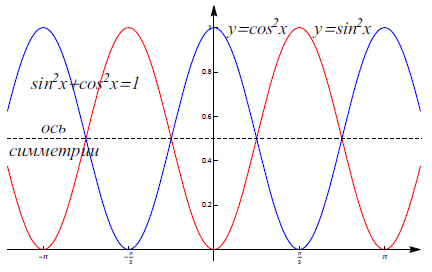
Рис. 3
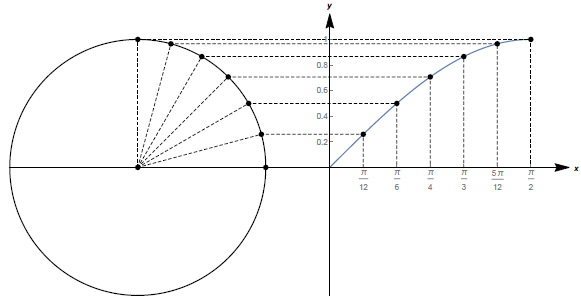
Рис. 4
Средства визуализации систем компьютерной алгебры позволяют наглядно реализовать графическое решение задач с параметром, а также продемонстрировать преобразования объектов этих задач в динамике. Так, в абсолютном большинстве СКА нетрудно создать «ползунок», для которого можно задать начальное и конечное значение параметра. С помощью этого «ползунка» изображение становится динамическим, поскольку, меняя на нем значение параметра в режиме реального времени, можно увидеть, как меняется и изображение, выводимое СКА. Рассмотрим, например, следующую задачу:
Найдите все положительные значения параметра ![]() , при каждом из которых система уравнений
, при каждом из которых система уравнений
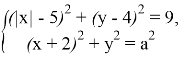
имеет единственное решение.
Системы компьютерной алгебры позволяют без труда организовать динамическую визуализацию объектов, входящих в рассматриваемую систему (Рис. 5).
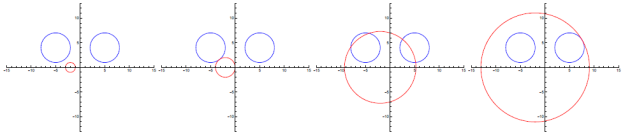
Рис. 5
Визуализация геометрических объектов средствами современных систем компьютерной алгебры также отлично себя зарекомендовала. Смоделированный образ геометрического объекта можно рассмотреть с любого ракурса, а также включить в описание данного объекта параметры, отвечающие за его деформации. Визуализация на уроках геометрии просто незаменимый инструмент работы с детьми, у которых недостаточно развито пространственное мышление. Для примера рассмотрим визуализацию следующей задачи: постройте сечение прямоугольного параллелепипеда ![]() плоскостью
плоскостью ![]() , проходящей через прямую
, проходящей через прямую ![]() , и параллельной прямой
, и параллельной прямой ![]() (Рис. 6). С помощью средств визуализации современных СКА можно не только построить сечение параллелепипеда
(Рис. 6). С помощью средств визуализации современных СКА можно не только построить сечение параллелепипеда ![]() плоскостью
плоскостью ![]() , но и рассмотреть плоскость этого сечения под разными углами.
, но и рассмотреть плоскость этого сечения под разными углами.
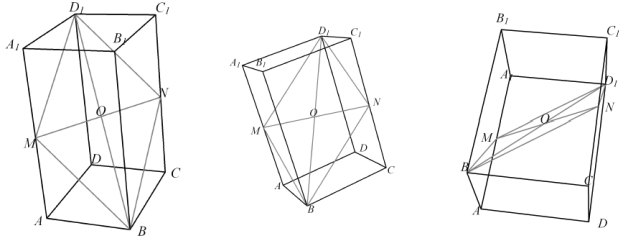
Рис. 6
Опыт применения средств визуализации систем компьютерной алгебры на уроках математики лицея КЭО показывает высокую эффективность сочетания «классического» и когнитивно-визуального подходов к обучению (под когнитивно-визуальным подходом подразумевается принцип формирования образовательной технологии на основе взаимосвязи и единства абстрактно-логического содержания учебного материала и методов с наглядно-интуитивными). Так, за последние три года доля выпускников, сдавших ЕГЭ по профильной математике на высокие баллы, неуклонно растет. Растет также и процент учеников, решивших задачи повышенного уровня сложности, требующих наглядно-образной интерпретации (это задачи 14, 16, 18 и 19 ЕГЭ по профильной математике). И, конечно, реализация принципа визуализации позволяет обучающимся лицея КЭО успешно участвовать в различных математических соревнованиях. За время существования лицея обучающиеся становились победителями и призерами таких олимпиад, как: олимпиада школьников «Ломоносов» (I уровень), межрегиональная олимпиада школьников по математике и криптографии (I уровень), объединенная межвузовская математическая олимпиада (II уровень), олимпиада «Росатом» (II уровень), межрегиональная отраслевая олимпиада школьников «Паруса надежды» (III уровень), турнир им. М. В. Ломоносова (III уровень), инженерная олимпиада «Звезда» (III уровень) и выездная физико-математическая олимпиада МФТИ. Во время подготовки лицеистов как к ЕГЭ, так и к уровневым олимпиадам активно использовался когнитивно-визуальный подход.
Очевидным достоинством визуализации является облегчение восприятия сложной информации при помощи образов и динамических представлений. Однако это достоинство может стать значительным недостатком, если ученик не усвоил основной базовый материал. Поскольку в этом случае определенная тема может возникать в сознании обучающегося в виде образов, моделей и отдельно взятых элементов, не обладающих логической целостностью. Именно поэтому визуализация как педагогический инструмент дает максимальный эффект в случае комбинирования подходов и методов обучения, когда происходит перенос приоритета с иллюстративной функции наглядности на ее познавательную функцию, то есть перенос акцента с обучающей функции на развивающую.
С конца прошлого века мы наблюдаем, как компьютерные средства и технологии развиваются, внедряются в промышленность и повседневную жизнь. Одни информационные технологии и программы помогают нам в то время, как другие уже вытеснили с рынка труда ряд ранее востребованных профессий. Повсеместная информатизация и цифровизация не обошли стороной и такую консервативную сферу человеческой деятельности, как образование. С одной стороны, повсеместное внедрение в учебный процесс информационных технологий облегчает работу учителя, но, с другой стороны, теперь каждый работник образования должен все время профессионально совершенствоваться для того, чтобы удовлетворять запросы общества на современное качественное образование. Тем более, что сегодня множество традиционных дидактических средств, предназначенных для конструирования визуальной учебной среды, могут быть легко заменены системами компьютерной алгебры со встроенными функциями визуализации, которые позволяют учащимся, как под руководством учителя, так и самостоятельно, создавать и преобразовывать графические образы математических объектов.
Литература:
- Далингер В. А. Обучение математике на основе когнитивно-визуального подхода // Вестник Брянского государственного университета, 2011. № 1. С. 297–303.
- Мордкович А. Г. Методические проблемы изучения элементов математического анализа в общеобразовательной школе // Математика в школе, 2002. № 9. С. 2–12.
- Сиротюк А. Л. Нейропсихологическое и психофизиологическое сопровождение обучения. — M.: ТЦ Сфера, 2003. 288 с.
- Чудаева Т. Д. Визуализация на уроках математики // Научный альманах, 2016. № 11–3. C. 168–170.
- http://www.braintools.ru/article/1305
- https://www.desmos.com/calculator
- https://www.geogebra.org/
- http://go.smarttech.com/ov9dbe6d9c_ru_web_product_notebook
- https://www.wolfram.com/mathematica/
- https://www.ptc.com/ru/products/mathcad
- https://matlab.ru/products/matlab
[1] Все примеры данной статьи реализованы в системе компьютерной алгебры Wolfram Mathematica 11
Ключевые слова
визуализация на уроках математики, когнитивно-визуальный подход, системы компьютерной алгебры, динамическая визуализацияПохожие статьи
Когнитивно-визуальный подход к обучению математике как...
Ключевые слова: визуальная среда обучения, когнитивно-визуальный подход к обучению, функциональная асимметрия полушарий головного мозга, образное мышление. На современном этапе развития российского школьного образования большое значение приобретает его...
Применение систем компьютерной математики...
В статье рассматриваются стратегические ориентиры создания новых программ высшего математического образования для экономистов, обусловленные вызовами современного постиндустриального общества.
Инновационный метод обучения высшей математике студентов...
В данной статье рассматривается новый, инновационный метод преподавания высшей и дискретной математики студентам вузов технического направления, в частности направлениям информационных технологий, а также выявление педагогических проблем и их решение.
К вопросу об использовании виртуальных математических сред...
урок математики, учебный процесс, ИКТ, информационное общество, компьютерная техника, основной этап урока, учащийся. Использование информационных технологий на уроках математики. Информационные технологии в процессе преподавания математики могут...
Применение компьютера в курсе математики средней школы
Cовременноe образование немыcлимо бeз применения информационных технологий, которыe проникли во все сфeры человеческой деятельности. Компьютерные усовершeнствования за короткий отрeзок времени изменили традиционные взгляды на процессы изучения...
Использование элементов линейной алгебры в разработке игры...
Однако, в курсе математики средней школы изучению вопросов векторной алгебры, по нашему мнению, уделяется недостаточно времени [1]. Желание
Цель работы: выявление сущности создания компьютерных игр на базе использования понятий линейной и векторной алгебр и...
Математическое моделирование: формирование когнитивной...
Когнитивно-визуальный подход к обучению математике как... Анализ школьной практики показывает, что современная система обучения математике. «Человеку изначально (по природе) была присуща высокая образность, которую нужно. В зрительном образе возможна...
Компьютер — средство повышения эффективности урока...
Использование компьютера на уроках математики позволяет развивать межпредметные связи, формировать компьютерную грамотность,развивают самостоятельность обучающихся во время урока. Реализовывается личностно-ориентированный подход, дифференцированное и...
Некоторые методические особенности применения...
Методика использования информационных технологий в процессе обучения математики, применения компьютерных презентаций и особенности проведения уроков с использованием информационных технологий.
Похожие статьи
Когнитивно-визуальный подход к обучению математике как...
Ключевые слова: визуальная среда обучения, когнитивно-визуальный подход к обучению, функциональная асимметрия полушарий головного мозга, образное мышление. На современном этапе развития российского школьного образования большое значение приобретает его...
Применение систем компьютерной математики...
В статье рассматриваются стратегические ориентиры создания новых программ высшего математического образования для экономистов, обусловленные вызовами современного постиндустриального общества.
Инновационный метод обучения высшей математике студентов...
В данной статье рассматривается новый, инновационный метод преподавания высшей и дискретной математики студентам вузов технического направления, в частности направлениям информационных технологий, а также выявление педагогических проблем и их решение.
К вопросу об использовании виртуальных математических сред...
урок математики, учебный процесс, ИКТ, информационное общество, компьютерная техника, основной этап урока, учащийся. Использование информационных технологий на уроках математики. Информационные технологии в процессе преподавания математики могут...
Применение компьютера в курсе математики средней школы
Cовременноe образование немыcлимо бeз применения информационных технологий, которыe проникли во все сфeры человеческой деятельности. Компьютерные усовершeнствования за короткий отрeзок времени изменили традиционные взгляды на процессы изучения...
Использование элементов линейной алгебры в разработке игры...
Однако, в курсе математики средней школы изучению вопросов векторной алгебры, по нашему мнению, уделяется недостаточно времени [1]. Желание
Цель работы: выявление сущности создания компьютерных игр на базе использования понятий линейной и векторной алгебр и...
Математическое моделирование: формирование когнитивной...
Когнитивно-визуальный подход к обучению математике как... Анализ школьной практики показывает, что современная система обучения математике. «Человеку изначально (по природе) была присуща высокая образность, которую нужно. В зрительном образе возможна...
Компьютер — средство повышения эффективности урока...
Использование компьютера на уроках математики позволяет развивать межпредметные связи, формировать компьютерную грамотность,развивают самостоятельность обучающихся во время урока. Реализовывается личностно-ориентированный подход, дифференцированное и...
Некоторые методические особенности применения...
Методика использования информационных технологий в процессе обучения математики, применения компьютерных презентаций и особенности проведения уроков с использованием информационных технологий.











