Приёмы смыслового чтения как средство обучения решению текстовых задач в 1–2 классах
Авторы: Сазонова Людмила Викторовна, Жданова Светлана Михайловна
Рубрика: 5. Педагогика общеобразовательной школы
Опубликовано в
Дата публикации: 23.02.2016
Статья просмотрена: 2094 раза
Библиографическое описание:
Сазонова, Л. В. Приёмы смыслового чтения как средство обучения решению текстовых задач в 1–2 классах / Л. В. Сазонова, С. М. Жданова. — Текст : непосредственный // Актуальные вопросы современной педагогики : материалы VIII Междунар. науч. конф. (г. Самара, март 2016 г.). — Самара : ООО "Издательство АСГАРД", 2016. — С. 181-187. — URL: https://moluch.ru/conf/ped/archive/188/9829/ (дата обращения: 27.04.2024).
Эти добрые люди и не подозревают, каких трудов и времени стоит научиться читать. Я сам на это употребил 80 лет и все не могу сказать, чтобы вполне достиг цели.
И. Гете
Развитие личности в системе образования обеспечивается, прежде всего, через формирование универсальных учебных действий. Овладение учащимися универсальными учебными действиями создаёт возможность самостоятельного успешного усвоения новых знаний, умений и компетентностей, включая организацию усвоения, т. е. умение учиться.
Понять содержание текста — важная и одновременно сложная задача.
Мы должны научить своих учеников:
ориентироваться в содержании текста и понимать его целостный смысл, находить в тексте требуемую информацию (пробегать текст глазами, определять его основные элементы, сопоставлять формы выражения информации в запросе и в самом тексте, устанавливать, являются ли они тождественными или синонимическими, находить необходимую единицу информации в тексте);
преобразовывать текст, используя новые формы представления информации: формулы, графики, диаграммы, таблицы (в том числе динамические, электронные, в частности в практических задачах), переходить от одного представления данных к другому;
решать учебно-познавательные и учебно-практические задачи, требующие полного и критического понимания текста:
на основе имеющихся знаний, жизненного опыта подвергать сомнению достоверность получаемой информации, обнаруживать её недостоверность.
Для формирования вышеперечисленных универсальных учебных действий, используются приёмы смыслового чтения. Стратегии смыслового чтения чётко прослеживаются в этапах работы над решением текстовых задач на уроках математики.
|
Стратегии смыслового чтения |
Этапы решения задач |
Что должен уметь ученик |
|
Поиск информации и понимание прочитанного |
Анализ содержания задачи. Поиск пути решения задачи и составление плана ее решения |
Ориентироваться в содержании текста и понимать его целостный смысл находить в тексте требуемую информацию |
|
Преобразование и интерпретация |
Осуществление плана решения задачи. |
Преобразовывать текст, используя новые формы представления информации |
|
Оценка информации |
Проверка решения задачи |
Подвергать сомнению достоверность получаемой информации, обнаруживать её |
Решение любой текстовой задачи состоит из нескольких этапов: восприятие и первичный анализ задачи, поиск и составление плана решения, выполнение решения и получение ответа на вопрос, проверка решения, формулировка окончательного ответа, дополнительная работа над решенной задачей.
Основная цель на первом этапе — это понять задачу и преобразовывать текст, используя новые формы представления информации.
Полезно после чтения задачи предложить учащимся представить себе то, о чём говорится в задаче и предложить нарисовать словесную картинку. Далее разбиение текста на смысловые части и выделение на этой основе необходимой для поиска решения информации.
Например: «Утром в магазине было продано 30 книжных шкафов. К концу рабочего дня осталось 12 шкафов. Сколько шкафов продали за день?» — удобнее искать, если текст её будет сформулирован так: «Было 30 шкафов. Осталось 12 шкафов. Сколько шкафов продали?»
Выделение основных опорных слов, которые связаны с действием, соответствующим сюжету. Например: «На вешалке 8 пальто. Дети взяли 6 пальто. Сколько пальто осталось?» Основные слова — было, взяли, осталось.
Главная цель учителя состоит в том, чтобы научить каждого ученика при решении той или иной текстовой задачи понимать вопрос задачи, хорошо представлять её условие и правильно выбирать соответствующее действие. Существенную помощь в выборе действия при решении задачи может оказать использование схематических рисунков, являющихся некоторыми моделями задач. Рассмотрим задачи.
Задача 1. Петя нашёл в лесу 6 белых грибов и 5 подосиновиков. Сколько грибов нашёл Петя?
Сначала нарисуем 6 коричневых кружков. Каждый кружок означает 1 белый гриб. Так как Петя нашёл, кроме белых грибов, ещё 5 подосиновиков, то нарисуем ещё 5 красных кружков. Каждый красный кружок означает 1 подосиновик. Каждый нарисованный кружок означает 1 гриб (белый или подосиновик). Используя числа, данные в тексте задачи, можно сказать, что всего Петя нашёл 6 и 5 грибов, т. е. 6+5. Запишем решение 6+5=11. Ответ: 11 грибов.
![]()
Задача 2. Около школы посадили 9 деревьев — берёз и рябин. Берёз 4. Сколько рябин посадили около школы?
Нарисуем 9 зелёных кружков. Каждый зелёный кружок означает одно дерево (берёзу или рябину), посаженные около школы. Так как берёз посадили 4, то из нарисованных 9 кружков зачеркнём карандашом 4 кружка. Каждый зачёркнутый кружок означает одну берёзу. Остальные деревья — рябины. О рябинах можно сказать, что их 9 без 4, т. е. 9–4. Решение: 9–4=5 Ответ: 5 рябин.
![]()
Обучая решению любой задачи, необходимо выработать у детей такие умения: обозначать геометрической фигурой каждый предмет, о котором говорится в тексте задачи, и ответить на вопрос о том, что означает каждый нарисованный или зачёркнутый кружок; выразить зависимость искомого числа от известных (данных) в задаче чисел; записать решение задачи в виде равенства; найти результат и записать ответ.
Подготовка к решению задач может быть успешно начата с первых уроков математики. Рассмотрим задачу: «В избушке сидят коза и семеро козлят. Сколько всего животных в избушке?» Работа над задачей может быть проведена следующим образом. Учитель говорит: «В избушке сидят семеро козлят и слушают сказку, которую рассказывает им мама. Сейчас мы нарисуем картинку. Так как козу и козлят нарисовать сложно, мы красным кругом обозначим козу, а белым — козлят. Козу нарисуем в центре, а козлят — вокруг козы. Что обозначают кружки красного и белого цвета? Теперь давайте покажем всех животных. Концом карандаша проводится замкнутый контур, внутри которого оказывается 8 кругов. Сосчитайте все нарисованные круги. Сколько их? А сколько всего животных?
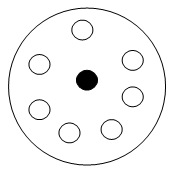
Решение пока не записывается. Под рисунком можно подписать ответ — число 8.
В 1 классе учащиеся встречаются с разными задачами, решаемыми с помощью одного действия.
Рассмотрим задачу на увеличение числа на несколько единиц.
Задача. «У Коли было 5 марок, а у Феди на 3 марки больше. Сколько марок было у Феди?»
Сначала учитель знакомит учащихся с полным текстом задачи. А затем читают задачу по частям. Прежде чем рисовать геометрические фигуры, он выясняет, как удобнее их изобразить. Очевидно, рисовать все фигуры в одну строку неудобно. Так как неизвестно, сколько марок у Феди? Поэтому фигуры лучше нарисовать парами. Например, в две строки, располагая их одну под другой. Итак, у Коли было 5 марок. Нарисуем в верхней строке 5 красных кругов. Каждый красный кружок означает одну марку, которая была у Коли. У Феди было на 3 марки больше. Это значит, что у Феди было столько же марок, сколько у Коли, да ещё 3.Поэтому во второй строке нарисуем синих кружков столько же, сколько красных, т. е. 5, да ещё 3. Каждый синий кружок означает одну марку Феди. Запишем: 5+3=8. Ответ: 8 марок.

Задачи на уменьшение числа на несколько единиц.
Задача. В зоологическом саду живут 6 жирафов, а верблюдов на 2 меньше. Сколько верблюдов в зоологическом саду?
Сначала выясняется, что круги удобнее рисовать, располагая их парами. Нарисуем 6 жёлтых кругов. Каждый жёлтый круг означает одного жирафа. О верблюдах сказано, что их было на 2 меньше. Это значит, что верблюдов столько же, сколько жирафов, но без двух. Для того чтобы их нарисовать, в верхней строке отделим чёрточкой 2 круга, а в нижней строке нарисуем коричневые круги до сделанной отметки. Каждый коричневый круг означает одного верблюда. Верблюдов 6 без 2, т. е. 4. Решение: 6–2=4. Ответ: 4 верблюда.

Описанная работа представляется важной для дальнейшего обучения. Умение отвечать на вопросы способствует осознанному усвоению. Разъяснения, которые дают учащиеся, развивают речь.
На втором этапе важно находить и устанавливать связи между данными и искомым и на этой основе выбирать арифметическое действие. На данном этапе используются различные способы моделирования.
Например (предметное моделирование) Задача: «У Лены было 6 карандашей, а у Тани 4 карандаша. Сколько карандашей у обеих девочек?» К доске выходят две девочки. У одной из них в руке 6 карандашей, у другой — 4 карандаша. Такое воспроизведение уточняет представления детей, возникшие при восприятии ими задачи.
Моделирование как важное средство решения задач.
(преобразовывать текст, используя новые или иные формы представления информации)
Что же понимается под моделированием условия задачи? Моделирование в широком смысле слова — это замена действий с реальными предметами действиями с их уменьшенными образцами, моделями, муляжами, макетами, а также их графическими заменителями: рисунками, чертежами, схемами. Рисунки могут изображать реальные предметы или же быть условными, схематичными, т. е. изображать реальные предметы условно, в виде различных фигур: квадратов, кружков, прямоугольников.
Чертёж представляет собой условное изображение предметов, взаимосвязей между ними и взаимоотношения величин с помощью отрезков и с соблюдением определённого масштаба.
Чертёж, на котором взаимосвязи и взаимоотношения передаются приблизительно, без точного соблюдения масштаба, называется схематическим чертежом, или схемой.
Предметное и графическое моделирование математической ситуации при решении текстовых задач давно применяется в школьной практике. Графическая наглядность необходима на всём протяжении обучения как важное средство развития критического мышления.
Процесс составления текстовых задач по различным моделям предполагает формулирование высказывательной модели задачи. Под составлением задачи понимают: результат соответствующего процесса (словесная модель); механизм составления задачи, приводящий к формулировке текста.
В процессе работы над данным видом деятельности целесообразно использовать следующий алгоритм.
- Придумай сюжет задачи.
- Назови объекты, о которых говорится в задаче.
- Укажи количественные (качественные) характеристики объектов (установи отношения).
- Сформулируй требование задачи.
- Смоделируй текст задачи.
Рассмотрим методику составления текстовых задач по различным моделям.
Модель 1. Условный рисунок. Используем с 1 класса
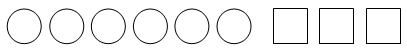
|
Этап словесного моделирования задачи |
Последовательность выполнения действий |
|
Придумаю сюжет задачи |
О книгах, стоящих на полках |
|
Назову объекты задачи |
Полки с книгами |
|
Укажу количественные характеристики |
На первой полке 6 книг, на второй -3 |
|
Сформулирую требование задачи |
Сколько всего книг на полке? |
|
Смоделирую текст задачи |
На одной полке 6 книг, на другой- 3. Сколько всего книг было на двух полках? |
Модель 2. Краткая запись. Используем с 1 класса
Было — 15
Выпили — 4 и 5
Осталось -?
|
Этап словесного моделирования задачи |
Последовательность выполнения действий |
|
Придумаю сюжет задачи |
О компоте в кастрюле |
|
Назову объекты задачи |
Стаканы с компотом |
|
Укажу количественные характеристики |
15 стаканов было в кастрюле; 4 стакана компота выпили утром; 5 стаканов компота выпили в обед |
|
Сформулирую требование задачи |
Сколько стаканов компота осталось в кастрюле? |
|
Смоделирую текст задачи |
В кастрюле было 15 стаканов компота. Утром выпили 4 стакана, в обед — 5 стаканов. Сколько стаканов компота осталось в кастрюле? |
Модель 3. Схема. Используем в 1 классе
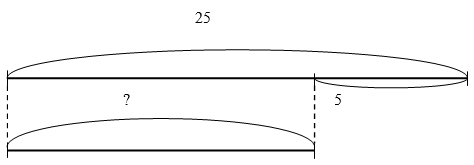
|
Этап словесного моделирования задачи |
Последовательность выполнения действий |
|
Придумаю сюжет задачи |
О количестве песен на кассетах |
|
Назову объекты задачи |
Кассеты |
|
Укажу количественные характеристики |
На одной кассете записано 25 песен, их на 5 больше, чем на второй кассете |
|
Сформулирую требование задачи |
Сколько песен на другой кассете? |
|
Смоделирую текст задачи |
На одной кассете записано 25 песен, их на 5 больше, чем на другой. Сколько песен записано на другой кассете? |
Модель 4. Числовое выражение. Используем во 2 классе
50 + (50–14)
|
Этап словесного моделирования задачи |
Последовательность выполнения действий |
|
Придумаю сюжет задачи |
О массе проданных фруктов |
|
Назову объекты задачи |
Яблоки и груши |
|
Укажу количественные характеристики |
Яблок — 50 кг, груш — на 14 кг меньше, чем яблок |
|
Сформулирую требование задачи |
Сколько фруктов продано? |
|
Смоделирую текст задачи |
В магазине продали 50 кг яблок, а груш — на 14 кг меньше, чем яблок. Сколько всего фруктов продали? |
Как отмечает Л. Ш. Левенберг, «рисунки, схемы и чертежи не только помогают учащимся в сознательном выявлении скрытых зависимостей между величинами, но и побуждают активно мыслить, искать наиболее рациональные пути решения задач, помогают не только усваивать знания, но и овладевать умением применять их».
Так во 2 классе, анализируя задачу: «В первый день для ремонта дома привезли 28 брёвен, а во второй день привезли на 4 машинах по 10 брёвен. Сколько всего брёвен привезли за эти два дня?», обычно записывают её кратко в таком виде:
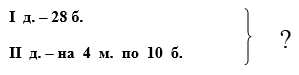
Такая модель не отражает жизненной ситуации с достаточной наглядностью, что и приводит к ошибкам в решении задачи. Поэтому необходимо смоделировать её условие в виде схематического рисунка:
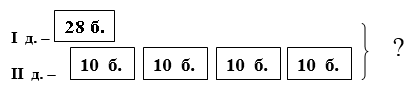
Такая модель отражает математическую ситуацию более наглядно. По такой модели даже слабый ученик сможет записать решение.

Проведя анализ понимания детьми текста задачи, пришли к выводу, что при использовании модели № 1(традиционной) 11 % учащихся затруднялись воспроизвести условие задачи, тогда как при использовании модели № 2 лишь 2 % имели затруднения. Исходя из этого, можно сделать вывод, что использование модели № 2 для задач данного вида более эффективно.
Рассмотрим задачу с пропорциональными величинами для 2 класса.
«В трёх одинаковых ящиках 21 кг апельсинов. Сколько килограммов апельсинов в 8 таких ящиках?» Обычно условие этой задачи записывается сразу в таблицу:
|
Масса одного ящика |
Количество ящиков |
Общая масса |
|
Одинаковая |
3 |
21 кг |
|
8 |
? |
Таблица — это тоже модель задачи, но более абстрактная, чем схематический рисунок или чертёж. При первичном знакомстве с этой задачей целесообразнее смоделировать её условие в виде схематического рисунка или чертежа.
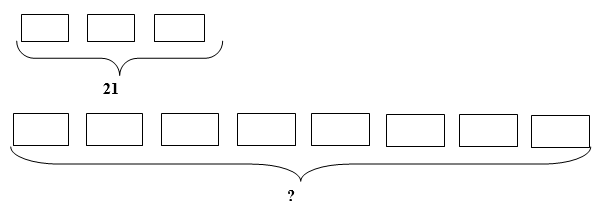
Так же проанализировав результаты понимания детьми задачи данного вида, пришли к заключению, что действительно схематический рисунок является самой удачной моделью, для записи условия задач данного вида, особенно на первичном этапе.

Только 4 % учащихся имели сложности при выборе решения задачи, тогда как при использовании таблицы процент был значительно выше — 14 %.
Рассмотрим ещё один из приёмов развития смыслового чтения — составление краткой записи условия задачи на части во 2 классе.
«Дочка младше мамы в 4 раза и младше бабушки в 9 раз. Сколько лет каждой, если вместе им 98 лет?»

Если меньшую величину обозначить за одну часть, тогда на возраст мамы приходится четыре такие части, на возраст бабушки девять частей. Из краткой записи условия понятен план решения задачи. Изображение одной части может быть любым.
Так как задачи данного вида очень сложны для второклассников, то очень важно, чтобы краткое условие было наиболее наглядно. Поэтому самой эффективной оказалась модель смыслового рисунка.
Представленная таблица, на наш взгляд, отражает наиболее оптимальные виды краткой записи задач с учётом возрастных и психологических особенностей младших школьников. Данные виды записи развивают мыслительные способности учащихся через рассуждения. Такой метод обучения имеет важное значение для формирования межпредметных компетенций.
|
Вид задачи |
Класс |
Вид записи |
|
на нахождение суммы; |
1 |
Условный рисунок |
|
на нахождение остатка; |
1 |
Условный рисунок |
|
на увеличение (уменьшение) числа на несколько единиц; |
1 |
Условный рисунок |
|
на нахождение суммы одинаковых слагаемых (произведения); |
2 |
Условный рисунок -чертёж |
|
на деление на равные части и деление по содержанию; |
2 |
Условный рисунок |
|
на нахождение стоимости товаров по известным цене и количеству; |
2 |
Смысловой рисунок |
|
на увеличение (уменьшение) числа в несколько раз; |
2 |
Смысловой рисунок |
|
составные задачи, решаемые двумя арифметическими действиями |
1–2 |
Схематический рисунок — чертёж |
Овладение стратегиями происходит преимущественно в группах или парах, что позволяет выработать у учеников не только речевую, но и коммуникативную компетентность.
Заключение
Учитывая стратегии современных подходов к чтению, можно рекомендовать учителям математики следующее:
выбирать наиболее рациональные виды чтения для усвоения учащимися нового материала;
формировать у учащихся интерес к чтению путем внедрения нестандартных форм и методов работы с текстом;
предвидеть возможные затруднения учащихся в тех или иных видах учебной деятельности;
повышать уровень самостоятельности учащихся в чтении по мере их продвижения вперед;
организовывать различные виды деятельности учащихся с целью развития у них творческого мышления;
обучать самоконтролю и самоорганизации в различных видах деятельности.
|
Класс |
Традиционная работа |
Использование стратегий смыслового чтения |
|
1 |
72 % |
96 % |
|
2 |
69 % |
96 % |
Представленные данные доказывают эффективность использования стратегий смыслового чтения на уроках математики.
Литература:
- Куропятник И. В. Чтение как стратегически важная компетентность для молодых людей// Педагогическая мастерская. Все для учителя. — 2012. — № 6
- Федеральный государственный образовательный стандарт основного общего образования.
- Формирование универсальных учебных действий в основной школе: от действия к мысли. Система заданий: пособие для учителя/под редакцией А. Г. Асмолова. — Москва 2013.
Похожие статьи
Обучение решению арифметических задач | Статья в журнале...
‒ чтение текста задачи учителем и учащимся; ‒ запись условия задачи
Схематическая форма записи.
Проверить словесно сформулированные задачи, производя действие над предметами.
К вопросу о формировании знаково-символических УУД...
Рис. 3. Схема-рисунок условия задачи. Запись условия задачи в таком виде не соответствует адекватному восприятию учащимися задачной ситуации и не способствует созданию образа, необходимого для фиксации связей между величинами.
Математическое моделирование в детском саду
«Стакан».
Задачи. Повышать интерес детей и родителей к математическому моделированию через игру и сказку. Создать условия для развития творческих способностей и творческой атмосферы.
1. Формулирование текста задачи по предложенному сюжету...
Поиск возможностей применения графического моделирования задачи привело к мысли использовать схему в
На этапе осмысления схематического чертежа можно использовать следующие приемы
Сюжеты задач разные. Рассуждения и решения идентичны.
Использование жизненного опыта обучающихся при решении...
2. Разбиение текста задачи на смысловые части.
Основное требование к чтению задачи — правильное чтение всех слов, сочетаний слов, соблюдение знаков препинания, правильная
5) умения переводить текстовые ситуации в предметные и схематические модели и обратно и др.
Обучение старших дошкольников решению арифметических задач
Простые задачи, т. е. задачи, решаемые одним действием, принято делить на следующие группы
В этих задачах арифметические действия как бы подсказаны самим условием задачи.
Задачи на переливание: от головоломки к алгоритму
В задачах на переливания требуется указать последовательность действий, при которой осуществляется требуемое переливание и выполнены все условия задачи.
Развивающие задачи как средство развития познавательных...
Учебная задача – это такая задача, решая которую ребенок усваивает общие принципы решения (т.е. обобщенный способ решения
Проектирование учебной деятельности младших школьников... Разграничивая моделирование процесса познания и моделирование задачи...
Логико-математическое развитие дошкольников средствами...
Решение задач комбинаторного типа способствует развитию подвижности мышления.
2 Моделирование фигур по словесному руководству.
2 Выполнение заданий по словесному указанию из двух исходных.
Похожие статьи
Обучение решению арифметических задач | Статья в журнале...
‒ чтение текста задачи учителем и учащимся; ‒ запись условия задачи
Схематическая форма записи.
Проверить словесно сформулированные задачи, производя действие над предметами.
К вопросу о формировании знаково-символических УУД...
Рис. 3. Схема-рисунок условия задачи. Запись условия задачи в таком виде не соответствует адекватному восприятию учащимися задачной ситуации и не способствует созданию образа, необходимого для фиксации связей между величинами.
Математическое моделирование в детском саду
«Стакан».
Задачи. Повышать интерес детей и родителей к математическому моделированию через игру и сказку. Создать условия для развития творческих способностей и творческой атмосферы.
1. Формулирование текста задачи по предложенному сюжету...
Поиск возможностей применения графического моделирования задачи привело к мысли использовать схему в
На этапе осмысления схематического чертежа можно использовать следующие приемы
Сюжеты задач разные. Рассуждения и решения идентичны.
Использование жизненного опыта обучающихся при решении...
2. Разбиение текста задачи на смысловые части.
Основное требование к чтению задачи — правильное чтение всех слов, сочетаний слов, соблюдение знаков препинания, правильная
5) умения переводить текстовые ситуации в предметные и схематические модели и обратно и др.
Обучение старших дошкольников решению арифметических задач
Простые задачи, т. е. задачи, решаемые одним действием, принято делить на следующие группы
В этих задачах арифметические действия как бы подсказаны самим условием задачи.
Задачи на переливание: от головоломки к алгоритму
В задачах на переливания требуется указать последовательность действий, при которой осуществляется требуемое переливание и выполнены все условия задачи.
Развивающие задачи как средство развития познавательных...
Учебная задача – это такая задача, решая которую ребенок усваивает общие принципы решения (т.е. обобщенный способ решения
Проектирование учебной деятельности младших школьников... Разграничивая моделирование процесса познания и моделирование задачи...
Логико-математическое развитие дошкольников средствами...
Решение задач комбинаторного типа способствует развитию подвижности мышления.
2 Моделирование фигур по словесному руководству.
2 Выполнение заданий по словесному указанию из двух исходных.











