Современные экономико-математические методы и модели в процессе принятия управленческих решений
Автор: Мясоедов Алексей Иванович
Рубрика: 14. Экономика и организация предприятия, управление предприятием
Опубликовано в
Дата публикации: 20.11.2017
Статья просмотрена: 2146 раз
Библиографическое описание:
Мясоедов, А. И. Современные экономико-математические методы и модели в процессе принятия управленческих решений / А. И. Мясоедов. — Текст : непосредственный // Проблемы и перспективы экономики и управления : материалы VI Междунар. науч. конф. (г. Санкт-Петербург, декабрь 2017 г.). — Санкт-Петербург : Свое издательство, 2017. — С. 150-153. — URL: https://moluch.ru/conf/econ/archive/263/13309/ (дата обращения: 26.04.2024).
Анализ и планирование деятельности организации являются главными компонентами в управлении, при этом анализ и планирование сочетаются с прогнозированием всех процессов в организации, помимо всего прочего они могут быть подконтрольны и тем самым выступать субъектом управления, что, как правило, приводит к улучшению качества процесса деятельности, либо они могут быть не подконтрольными, и, соответственно, их состояние не будет оказывать существенного воздействия на деятельность организации.
Анализ информации подразумевает, что, используя определенные процессы и закономерности, мы сможем их разделить по определенному признаку, с дальнейшим выявлением различного рода факторов и критериев, степени их влияния на сам процесс. Такой анализ, который сочетается с прогнозированием, будет одним из условий планирования деятельности организации, а также станет основанием для принятия различного рода управленческих решений.
Говоря об исследуемых процессах или наблюдаемых процессах, следует сделать ремарку на то что, в первую очередь, речь идёт о бизнес-процессах в деятельности современных организаций. Это подразумевает, прежде всего, совокупность работ по выполнению определенных задач, которые стоят перед организацией, основываясь на анализе хода выполнения этих процессов, влияния внешних условий, ее внутреннего состояния. Все это способствует тому, что на основе вышеуказанного, можно сделать определенные выводы о том, как вырабатываются и редактируются цели организации, а вместе с ними и управленческие решения [1]. В соответствии целевыми установками ставятся определенные задачи по планированию мероприятий с их последующей реализацией в процессе деятельности организации. При этом всегда используются критерии для оценки данных процессов, при принятии управленческих решений для реализации составленных планов.
Информация, которая необходима и используется при принятии управленческих решений часто достигает больших объемов и измеряется в десятках и сотнях мегабайт, достигая в крупных корпорациях или общегосударственных системах и более терабайт (1012байт). Информация всегда является многоаспектной и сложной, поскольку отражает суть объектов и систем, применяемых в организации, а также их взаимосвязи между собой.
Подобного рода обстоятельства давно вынудили современные организации прибегать к использованию программно-технического обеспечения, которое стало неотъемлемой составной частью их деятельности. Качественное применение подобного рода технологий приводит к выживаемости и комфортному развитию хозяйствующего субъекта в условиях конкурентной борьбы [2].
Распространение информационных технологий на данный момент достигло огромных масштабов. В любой сфере деятельности человека применяются подобного рода технологии, как простые, так и сложные. Большое распространение получили экономико-математические методы, которые позволяют моделировать различного рода ситуации, позволяют давать им оценку, прогнозировать их развитие, планировать деятельность организации в дальнейшем, выявлять закономерности и причинно-следственные связи между объектами и явлениями. Все это может в совокупности обеспечивать функционирование системы поддержки принятия решений для организаций любой сферы [3].
Принятие решений в системе управления на практике представляет собой проблему, которая отягощается различного рода альтернативами. Поэтому применение экономико-математических методов, можно рассматривать как эффективное средство структурированного анализа всей имеющейся информации с целью получения наиболее благоприятного исхода разрешения поставленных задач. Характерными особенностями применения экономико-математических методов является то, что для их построения учитываются все возможные факты вероятности успехов и рисков, которые позволяют сравнить результаты каждого из возможных принятых решений и выбрать наилучший вариант [4].
Использование экономико-математических методов и моделей является базовым инструментарием для принятия научно-обоснованных управленческих решений.
Проблемы принятия управленческих решений затрагивают сотрудников организации любого уровня, поэтому важно осознавать и понимать составляющие этого процесса так, чтобы решение, которое было принято, обеспечивало наилучший результат вне зависимости от должностного положения человека, принимающего эти решения [5].
Использование экономико-математических методов позволяет повысить качество как текущего, так и стратегического планирования, а дополнительный положительный эффект может быть достигнут без привлечения дополнительных ресурсов.
Далее будут рассмотрены некоторые упрощенные примеры реализации управленческого решения с использованием экономико-математических методов.
Пример A. Планировании производства— На предприятие производятся изделия трех типов: U1, U2, U3. По каждому типу изделия существует план (b1 b2 b3), по которому подрядчик обязан выполнить изделий в определенном количестве единиц. План может быть перевыполнен, но лишь в определенных границах, так как ресурсы компании ограничены (1, 2, 3). На каждое изделие уходит в определённое количество сырья, чьё количество подтипов составляет 4 единиц (1, 2, 3 4) Необходимо узнать, какое количество сырья каждого из подтипов сырья уйдет на изготовление каждого изделия.
Обозначаем ![]() количество подтипов сырья вида
количество подтипов сырья вида![]() , которое требуется на изготовление
, которое требуется на изготовление ![]()
![]() изделия. Первый индекс
изделия. Первый индекс ![]() у числа — вид сырья, второй — вид изделия. Значения представлены в таблице 1.
у числа — вид сырья, второй — вид изделия. Значения представлены в таблице 1.
Таблица 1

Изделие U1 приносит прибыль c1, U2 — прибыль c2, U3 — прибыль c3. Необходимо так прогнозировать производственный процесс, чтобы план был выполнен или перевыполнен, а суммарная прибыль была максимальной.
Поставленную задачу распишем в форме задачи линейного программирования. Элементами, такого решения будут x1, x2, x3 — количества изделий U1, U2, U3, которые будут произведены. Обязательность выполнения плана запишем в виде ограничений — неравенств:
![]() (1)
(1)
Отсутствие излишков изделий даст еще три ограничения-неравенства:
![]() (2)
(2)
Нам необходимо учитывать, что ресурсы сырья ограничены, поэтому по четырем подтипам сырья будем ещё четыре ограничения-неравенства:
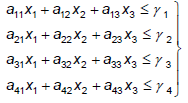 (3)
(3)
А прибыль, которая заявлена в плане (x1, x2, x3) будет равна
![]() (4)
(4)
Таким образом, мы получим задачу линейного программирования: подобрать такие значения переменных x1, x2, x3, чтобы они удовлетворяли неравенствам — ограничениям (1), (2), (3) и, при этом, обращали в максимум линейную функцию этих переменных:
![]()
![]() Пример B. Загрузка оборудования -Фирмы имеет два типа станков, из которых N1 станков тип№ 1 и N2 станков тип№ 2. Станки производят три типа продукции: Т1, Т2, Т3, производительность разница. Данные производительности станков даны в таблице 2.
Пример B. Загрузка оборудования -Фирмы имеет два типа станков, из которых N1 станков тип№ 1 и N2 станков тип№ 2. Станки производят три типа продукции: Т1, Т2, Т3, производительность разница. Данные производительности станков даны в таблице 2.
Таблица 2

Единица продукции типа Т1 приносит прибыль с1, типа Т2 — прибыль с2, типа Т3 — прибыль с3.
У фирмы существует план, по которому ей необходимо производить в месяц не менее b1 единиц типа Т1, не менее b2 единиц типа Т2, не менее b3 единиц типа Т3. Количество выпускаемых типов продукции не должны быть выше 1, 2, 3, при этом все станки должны работать. Необходимо распределить работу станков так, чтобы производство продукции вида Т1, Т2, Т3, приносило максимальный месячный доход.
В данной задаче элементы решения — не количества продукции определенного типа, а количества станков типа № 1 и типа № 2, которые заняты производством. Будет удобнее обозначить элементы решения x с двумя индексами. Всего будет шесть элементов решения:
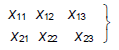 5)
5)
Здесь x11 — количество станков типа № 1, занятых изготовлением продукции Т1, x12 — количество станков типа № 1, занятых изготовлением продукции Т2, и т. д.
![]() Это задача линейного программирования. Необходимо указать условия ограничения, наложенные на элементы. Выполнения, даст нам три неравенства-ограничения:
Это задача линейного программирования. Необходимо указать условия ограничения, наложенные на элементы. Выполнения, даст нам три неравенства-ограничения:
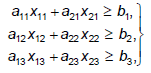 (6)
(6)
Перевыполнение, даст ещё три неравенства-ограничения:
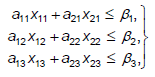 (7)
(7)
Ограничения, которые связанны с наличием оборудования и его полной загрузкой — это суммарное количество станков типа № 1, которые заняты изготавливая всю продукцию, должно быть равно N1, а для типа № 2 — N2, что дает два условия –равенства:
![]() (8)
(8)
Суммарный доход от производства — это суммарное количество продукции типа Т1, которое произведено всеми станками, будет равно a11 x11 + a21 x21 и принесет доход с1 (a11 x11 + a21 x21). Аналогично сказанному — суммарный доход фирмы за месяц при плане (5):
![]()
Или более краткая запись:
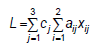
Линейная функция шести аргументов должны быть обращена к максимуму:
![]()
Так задача линейного программирования сводится к тому, чтобы найти такие значения переменных x11, x12, …, x23, которые бы, во-первых, удовлетворяли ограничениям-неравенствам (6), (7), во-вторых, — ограничениям-равенствам (8), и обращали бы в максимуме линейную функцию этих переменных (9), так в поставленной задаче линейного программирования существует шесть ограничений неравенств и два ограничения-равенства.
Таким образом, даже иллюстрация несложных примеров решения поставленных задач при помощи методов линейного программирования, позволила заключить, что они позволяют довольно быстро и эффективно принять правильное управленческое решение.
Исходя из всего вышесказанного можно сделать следующие выводы, что:
- Процесс принятия управленческих решений, в первую очередь, связан со сложной аналитическо-статистической работой, которая в современных условиях глобализации и большого объема информации, невозможен без использования различного рода программ и технических средств.
- Для обработки данных по исследованиям в данной области необходимо использовать формат математического моделирования на базе новых информационных технологий.
- Технологий, которые достигли за последнее время качественно нового уровня, очень сильно расширяют возможности эффективного управления и представляют небывалый интерес со стороны финансистов, руководителей производства, менеджеров, маркетологов, а новейшие методы обработки и анализа информации, просто необходимы для принятия качественного управленческого решения.
Литература:
- Острик А. А., Пряжникова Е. Ю. Когнитивные технологии на этапе освоения профессии // В книге: Горизонты зрелости Сборник тезисов участников Пятой всероссийской научно-практической конференции по психологии развития. Редакторы: Л. Ф. Обухова, И. В. Шаповаленко, М. А. Одинцова. 2015. С. 235–239.
- Колпаков В. Ф., Идентификация динамических моделей экономики//Модернизация национальной экономики: проблемы и решения: коллективная монография/под общей редакцией Н. А. Адамова. -М.: ЭКЦ «Профессор», 2014.
- Колпаков В. Ф. Исследование динамических свойств экономических систем с помощью весовых функций//Финансовая аналитика: проблемы и решения. -2015. -№ 13(247). -С. 56–64.
- Радостева, М. В. Производительность труда как фактор экономического роста//Исследование отношений, механизмов и институтов рынка: вопросы экономики и управления: сб. научных трудов. Вып. 5 -М.: Изд-во Московского гуманитарного университета, 2003.
- Колпаков В. Ф. Моделирование динамических процессов в экономике. Научно-практический и информационно-аналитический сборник «Финансовая аналитика», 2014.
Похожие статьи
Линейное программирование | Статья в журнале «Молодой...»
В данной статье рассматривается задача линейного программирования и возможный способ её решения — симплекс метод. Приведены примеры, поясняющие, что такое линейное программирование и симплекс метод.
Применение метода линейного программирования для решения...
Цель настоящей статьи — показать использование метода линейного программирования при решении текстовых задач по математике, предполагающих максимизацию (минимизацию) некоторой величины, например...
Предельная эффективность и параметрический анализ в задачах...
Решение задачи линейного программирования в Excel позволяет получить оптимальное решение и попутно создается отчет по устойчивости, который содержит двойственные оценки полученного решения.
Приложения линейного программирования к решению...
Метод решения рассматриваемых ниже задач связан с именем российского Лауреата Нобелевской премии по экономике Л. В. Канторовича (за вклад в теорию оптимального распределения ресурсов; 1975 г.; взгляд на математику как на единую дисциплину...
Создание и использование программы для статистического...
Получена задача линейного программирования: найти максимум целевой функции (4) при ограничениях (3).
При этом используются встроенные функции: МАКС, МИН, ЕСЛИ и ПОИСК РЕШЕНИЯ. Решение игровых задач с нулевой суммой с помощью Microsoft...
Решение интервальной задачи дробно-линейного...
В настоящее время широко разработаны вопросы традиционной оптимизации систем с детерминированными параметрами [1,2]. С математической точки зрения такая оптимизация есть отыскание экстремумов функции, параметры которых детерминированные...
Решение многокритериальных задач линейного...
Ключевые слова: задача линейного программирования, многокритериальная оптимизация, метод последовательных уступок. Метод последовательных уступок решения многокритериальных задач применяется в случае...
Решение транспортных задач с применением программирования...
Рассматриваются основные методы решения различных типов транспортных задач.
Ключевые слова:линейное программирование, транспортная задача, система автоматизированного проектирования, MathCAD, программирование.
Решение транспортных задач с помощью линейного...
Линейное программирование | Статья в журнале «Молодой...» Модель линейного программирования имела бы множество переменных решений, которые. Исторически общая задача линейного программирования была впервые поставлена в 1947.
Похожие статьи
Линейное программирование | Статья в журнале «Молодой...»
В данной статье рассматривается задача линейного программирования и возможный способ её решения — симплекс метод. Приведены примеры, поясняющие, что такое линейное программирование и симплекс метод.
Применение метода линейного программирования для решения...
Цель настоящей статьи — показать использование метода линейного программирования при решении текстовых задач по математике, предполагающих максимизацию (минимизацию) некоторой величины, например...
Предельная эффективность и параметрический анализ в задачах...
Решение задачи линейного программирования в Excel позволяет получить оптимальное решение и попутно создается отчет по устойчивости, который содержит двойственные оценки полученного решения.
Приложения линейного программирования к решению...
Метод решения рассматриваемых ниже задач связан с именем российского Лауреата Нобелевской премии по экономике Л. В. Канторовича (за вклад в теорию оптимального распределения ресурсов; 1975 г.; взгляд на математику как на единую дисциплину...
Создание и использование программы для статистического...
Получена задача линейного программирования: найти максимум целевой функции (4) при ограничениях (3).
При этом используются встроенные функции: МАКС, МИН, ЕСЛИ и ПОИСК РЕШЕНИЯ. Решение игровых задач с нулевой суммой с помощью Microsoft...
Решение интервальной задачи дробно-линейного...
В настоящее время широко разработаны вопросы традиционной оптимизации систем с детерминированными параметрами [1,2]. С математической точки зрения такая оптимизация есть отыскание экстремумов функции, параметры которых детерминированные...
Решение многокритериальных задач линейного...
Ключевые слова: задача линейного программирования, многокритериальная оптимизация, метод последовательных уступок. Метод последовательных уступок решения многокритериальных задач применяется в случае...
Решение транспортных задач с применением программирования...
Рассматриваются основные методы решения различных типов транспортных задач.
Ключевые слова:линейное программирование, транспортная задача, система автоматизированного проектирования, MathCAD, программирование.
Решение транспортных задач с помощью линейного...
Линейное программирование | Статья в журнале «Молодой...» Модель линейного программирования имела бы множество переменных решений, которые. Исторически общая задача линейного программирования была впервые поставлена в 1947.











