Ключевые слова: логическое мышление школьников, примеры упражнений на развитие логики.
В наше время, нам часто не хватает умения логично излагать свои мысли, особенно, если для нас важен результат этого изложения. Эта способность к логическому рассуждению не заложена в нас природой. Ее нужно развивать собственными усилиями. Каждый урок развивает логическое мышление, но дети часто не умеют делать обобщений, выводов, классификаций. В данной статье, я хочу уделить внимание тому, как важно развить логическое мышление обучающихся.
Для начала, выясним, что же такое логика и логическое мышление. Для этого воспользуемся толковым словарем В. И. Даля.
Логика, если дословно переводить с древнегреческого, обозначает речь, рассуждение. Если слово логика использовать как термин, то это наука о правильном мышлении, искусство рассуждения.
Логическое мышление — это вид мыслительного процесса, при котором человек использует логические конструкции и готовые понятия.
Вернемся к цели моей статьи и выясним, как же все-таки развить логическое мышление у детей средней школы на уроках математики?
Развитие логического мышления при изучении математики состоит в формировании у учащихся характерных для этого предмета приемов мыслительной деятельности. При этом важно, чтобы в структуру умственной деятельности школьников помимо алгоритмических умений и навыков, фиксированных в стандартных правилах, формулах и способах действий, вошли эвристические приемы, которые необходимы для решения творческих задач, применение знаний в новых ситуациях, доказательства высказываемых утверждений. Системное развитие логического мышления должно быть неотрывно от урока, каждый ученик должен принимать участие в процессе выполнения обучающей деятельности. Безусловно, данному процессу развития поможет решение задач. Решение всякой задачи по математике — это, прежде всего, цепь рассуждений. Вычисления, преобразования, построения, которыми так часто приходится пользоваться для решения задач, невозможны без логических рассуждений: они направляются рассуждениями. Значит, в математике невозможно обойтись без логики.
На уроках учитель должен моделировать ту умственную деятельность, которая нужна на данном этапе развития (учить анализировать задачи, делать чертежи, выявлять отношения объектов и т. д.). Это имеет обучающее и воспитывающее значение: учащиеся приобщаются к методу поиска, ориентируются не только на результат, но и на процесс его достижения, т. е. учатся мыслить логически.
В системе задач школьного курса математики, безусловно, необходимы задачи, направленные на отработку того или иного математического навыка, задачи иллюстративного характера, тренировочные упражнения, выполняемые по образцу. Необходимы специальные упражнения для обучения школьников способам самостоятельной деятельности, общим приемам решения задач, для овладения ими методами научного познания реальной действительности и приемам продуктивной умственной деятельности. Осуществляя целенаправленное обучение школьников решению задач, с помощью специально подобранных упражнений, можно учить их наблюдать, пользоваться аналогией, индукцией, сравнениями, и делать соответствующие выводы. Необходимо на уроках систематически использовать задачи, способствующие целенаправленному развитию творческого мышления учащихся, их математическому развитию, формированию у них познавательного интереса и самостоятельности. Такие задачи требуют от школьников наблюдательности, творчества и оригинальности. Также, в качестве средств развития логического мышления могут выступать занимательные задачи (задачи «на соображение», головоломки, нестандартные задачи, логические задачи). Почему же так хороши занимательные задачи?
Занимательный материал многообразен, но его объединяет следующее:
- способ решения занимательных задач не известен. Для их решения характерно, броуновское движение мысли, т. е. к решению приводит метод проб и ошибок. Поисковые пробы решения могут в отдельных случаях закончиться догадкой, которая представляет собой нахождение пути искомого решения.
- занимательные задачи способствуют поддержанию интереса к предмету и играют роль мотива к деятельности учащихся. Необычность сюжета, способа презентации задачи находят эмоциональный отклик у детей и ставят их в условия необходимости ее решения;
- занимательные задачи составлены на основе знаний законов мышления.
Систематическое применение задач такого вида способствует развитию мыслительных операций (анализ, синтез и др.) и формированию математических представлений детей.
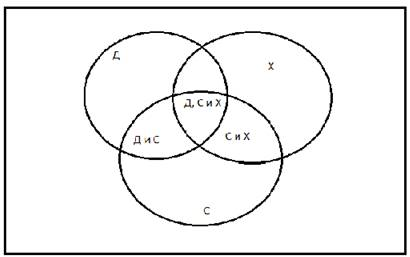
Пример занимательной задачи (решение осуществляется с помощью кругов Эйлера):
В пятых классах школы всего 70 детей, 27 из них занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. Сколько учащихся не посещают ни одного кружка?
Обозначения:
- Д — посещают драмкружок;
- С — спортсмены;
- Х– поют в хоре;
- ДХС — посещают одновременно 3 кружка
Как же все-таки использовать данную информацию на конкретном уроке?
По моему мнению, нужно выбрать задания, которые будут посильны для детей. Задания должны быть разнообразными для воздействия на различные высшие психические функции (например, память, мышление, речь, восприятие). Также необходимо выбрать задачу, которая потребует знание предыдущего материала (причем не только последней темы) и выполнения некоторых исследовательских действий. При задачах данного типа, все учащиеся должны быть включены в работу. Т. е. задачу прочитал один ученик, рассказал, о чем говорится в задаче другой, выявил отношения между предметами — третий и т. д. Далее, нужно предоставить детям возможность порассуждать: они должны записать в тетради предполагаемый ход решения, возможные действия и результат. После определенного времени, несколько из учащихся предлагают свои варианты (с объяснением) всему классу, а класс соглашается или нет, аргументируя свою точку зрения. Таким образом, каждый будет активным субъектом процесса обучения и у каждого будут развиваться как речь, так и приходить в порядок образ мыслей. В качестве домашнего задания, детям можно предложить попробовать составить свою задачу, похожую на классную.
Также, например, можно использовать упражнения следующего вида:
Пример 1. Найдите закономерность и допишите по одному примеру:
1) 1 = 12 1 + 3 = 22 1 + 3 + 5 = 32 …
2) 13 = 12 13 + 23 = (1 + 2)2 13 + 23 + 33 = (1 + 2 + 3)2 …
Решение:
1) Заметим, что нужно сложить нечетные цифры подряд и получится квадрат следующего четного числа: 1+3+5+7=42;
2) В левой части равенства последовательно складываются кубы чисел, а справа берется квадрат суммы тех же самых чисел, т. е. следующее равенство будет: 13+23+33+43=(1+2+3+4)2
Пример 2: Записаны подряд числа: 1, 2, 3, 4, 5,…, 2000.
Первое, третье, пятое, и т. д. по порядку вычёркивают, из оставшихся 1000 чисел снова вычёркивают первое, третье, пятое, и т. д., повторяя, пока не останется одно число. Что это за число?
Решение:
Выпишем ряды, для установления некоторой закономерности:
1) 1, 2, 3, 4, 5, 6, 7, …, 2000 (2000 чисел)
2) 2, 4, 6, 8, 10, …, 2000 (1000 чисел) формула 2n
3) 4, 8, 12, 16, 20, …, (500 чисел) формула 4n
Заметим, что остаются числа, являющиеся степенями двойки, а значит останется число:
2n < 2000, а это 210 = 1024, т. к. 211 = 2048 > 2000.
Логическое мышление — это тот конёк, который мобилизует работу всех компонентов усвоения — внимания, памяти, воображения, что составляет основу интеллекта учащихся, вовлекает учащегося познавательную деятельность, стимулируя тем самым и его логическое развитие. И педагоги, и родители должны постоянно помнить о том, что интеллектуальные способности — это тот багаж, с которым подросток выйдет во взрослую жизнь, с помощью которого выберет и освоит профессию.
Литература:
1. Фридман Л. М. Психолого-педагогические основы обучения математике в школе. — М.: Просвещение, 1983 г.
2. Даль В. И. Толковый словарь. — М.: Олма Медиа Групп, 2009 г.
3. Голощапова, С. В. Логические игры и задачи на уроках математике. — Я.: «Академия развития», 1997 г.

