Различают два типа оценивателей времени: оцениватель времени, управляемый решениями и не управляемый решениями. В первом типе информационные символы на выходе демодулятора рассматриваются как известная переданная последовательность, во втором — неизвестная.
Оценку параметра задержки, не управляемую решениями, можно получить путём усреднения отношения правдоподобия 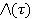 с учётом функции плотности вероятности (ФПВ) информационных символов для получения
с учётом функции плотности вероятности (ФПВ) информационных символов для получения 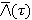 [1]. Затем это выражение дифференцируется по
[1]. Затем это выражение дифференцируется по 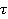 для получения условия для максимально правдоподобной (МП) оценки задержки, не управляемой решениями
для получения условия для максимально правдоподобной (МП) оценки задержки, не управляемой решениями 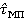 .
.
В случае двоичного (базового) амплитудно-модулированного (AM) сигнала, где информационные символы 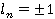 с равной вероятностью, усреднение по данным дает результат:
с равной вероятностью, усреднение по данным дает результат:
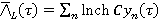 (1)
(1)
Он совпадает с результатом в случае оценивания фазы. Поскольку 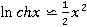 для малых x, квадратичная аппроксимация (9) предназначается для низких отношений сигнал/шум.
для малых x, квадратичная аппроксимация (9) предназначается для низких отношений сигнал/шум.
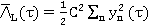 (2)
(2)
Для многоуровневой амплитудной модуляции (AM) мы можем аппроксимировать статистику информационных символов 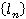 гауссовской функцией плотности вероятности (ФПВ) с нулевым средним и единичной дисперсией. Когда мы усредняем
гауссовской функцией плотности вероятности (ФПВ) с нулевым средним и единичной дисперсией. Когда мы усредняем 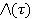 по гауссовской ФПВ, то получаем
по гауссовской ФПВ, то получаем 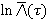 идентично
идентично 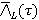 . Следовательно, оценку
. Следовательно, оценку 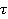 можно получить дифференцированием (2). Результат является аппроксимацией для МП оценки времени задержки без управления решениями. Производная от (2) приводит к результату (3).
можно получить дифференцированием (2). Результат является аппроксимацией для МП оценки времени задержки без управления решениями. Производная от (2) приводит к результату (3).
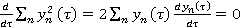 , (3)
, (3)
где 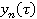 определено так:
определено так:
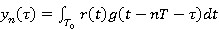 . (4)
. (4)
Схема отслеживающей петли, основанная на выражении (3), иллюстрируется на рисунке 1 [1].
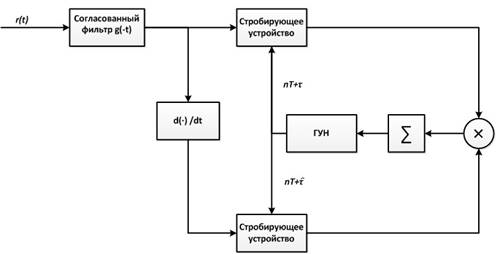
Рис. 1. Оценивание времени сдвига без обратной связи по решению для АМ в базовой полосе частот
В данной структуре суммирование служит петлевым фильтром. Полоса такого фильтра управляется длиной скользящего окна при суммировании. Выход петлевого фильтра подается на генератор управляемого напряжения (ГУН), который управляет интервалом стробирования на входе петли. Поскольку детектируемая информационная последовательность не используется при оценке задержки, оценивание оказывается не управляемым решением.
Для того чтобы восстановить переданную информацию в цифровой системе связи выход демодулятора должен периодически стробироваться со скоростью передачи символов в точно выбранных моментах 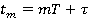 , где T — символьный интервал, а
, где T — символьный интервал, а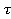 — номинальное время задержки, которое определяется временем распространения сигнала от передатчика к приёмнику. Поскольку время распространения от передатчика к приемнику обычно неизвестно на приеме, управление этим стробированием должно осуществляться от принимаемого сигнала [1].
— номинальное время задержки, которое определяется временем распространения сигнала от передатчика к приёмнику. Поскольку время распространения от передатчика к приемнику обычно неизвестно на приеме, управление этим стробированием должно осуществляться от принимаемого сигнала [1].
Чтобы выполнять это периодическое стробирование, требуется тактовая синхронизация (синхронизация символов) или восстановление отсчётов времени.
Восстановление отсчётов времени — одна из наиболее ответственных функций, которые выполняются в приёмнике синхронных цифровых систем связи. Отметим, что приёмник должен знать не только частоту (1/T), с которой стробируются выходы согласованных фильтров или корректоров, но также тот момент времени, в который необходимо взять отсчёты внутри каждого символьного интервала. Положение отсчётного момента внутри символьного интервала длительностью T называют фазой синхронизации.
Описание модели Matlab
Каждый, кто занимается цифровой обработкой сигналов, знает, как важно построить математическую модель проектируемого устройства, реализовать её в виде программы и затем провести на этой модели испытания в условиях, приближающихся к натурным.
Simulink является очень удобным средством решения таких задач для разных предметных областей и, в первую очередь, для задач в области цифровой обработки сигналов. MATLAB, Simulink и соответствующие продукты позволяют разрабатывать и моделировать системы связи. Использование Simulink во многих случаях исключает утомительные и трудоёмкие этапы составления и отладки программ, позволяя сосредоточить основные усилия непосредственно на решении определенных предметно-ориентированных задач. С помощью данной программы мы сможем количественно оценить эффективность моделируемой системы и аппаратных прототипов и сделать визуализацию данных [2].
Работая с программой Simulink, можно создавать модели линейных и нелинейных, аналоговых, дискретных и смешанных (аналогово-дискретных) цепей и систем, изменять параметры блоков непосредственно во время процесса моделирования и сразу же наблюдать реакцию моделируемой системы. Всё это делает работу с Simulink одинаково привлекательной как для начинающих пользователей, так и для опытных специалистов.
Именно поэтому для проведения моделирования и оценки параметра задержки была выбрана данная интерактивная графическая программа, позволяющая моделировать динамические системы на уровне структурных и функциональных схем.
Реализация схемы, изображенной на рисунке 1, в среде Matlab Simulink показано на рисунке 2.
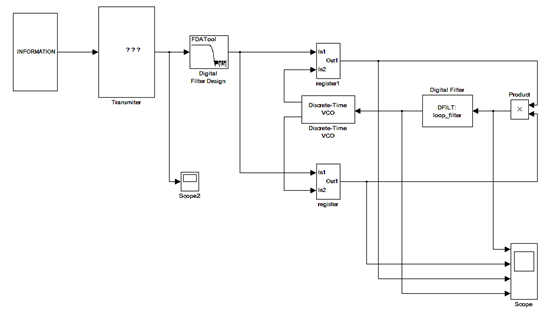
Рис. 2. Реализация схемы в Matlab Simulink
При моделировании отслеживающей петли в среде Matlab Simulink были заданы следующие параметры:
- Длительность информационного символа 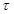 = 0.5/20 мкс
= 0.5/20 мкс
- Информационная частота fинф = 40 МГц
- Частота Доплера информационная Δfинф =200 Гц
- Промежуточная частота fпч = 400МГц
- Частота Доплера на промежуточной частоте Δfпч = 4 кГц
- Частота несущей fнес = 3 ГГц
Принимаемый сигнал является QPSK сигналом. Этот сигнал мы формируем при помощи блоков INFORMATION и Transmitter. Эти блоки представлены на рисунке 3 и 4.
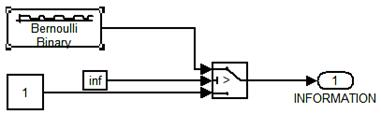
Рис. 3. Содержимое блока INFORMATION
Входным параметром блока INFORMATION является F=1/τ=20/(0.5e-6).
В качестве источника удобно использовать псевдослучайный некоррелированный битовый поток — блок Bernoulli Binary. Здесь мы задаем следующие параметры:
- Probability of a zero: 0.5;
- Initial seed: 64;
- Sample time: 1/(40e+6), где 40e+6 информационная частота. Это шаг модельного времени, использующийся для согласования работы источника и других компонентов модели во времени.

Рис. 4. Составные части блока Transmitter
Блок Unipolar to Bipolar Converter позволяет сделать из однополярного сигнала двуполярный. Здесь Repetition count: (3e+9) /(40e+6) =75, где в качестве входного параметра блока modulator PSK выступает параметр f=1/(40e+6), с информационной частотой fи=40 МГц.
Полученный QPSK сигнал мы можем увидеть по результатам моделирования на осциллографе Scope2, изображенный на рисунке 5.
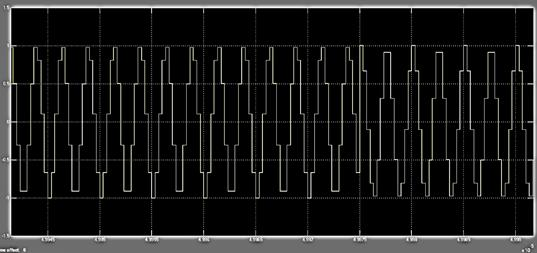
Рис. 5. Показания осциллографа Scope2
С помощью блока Digital Filter Design мы смоделировали КИХ-фильтр (ФНЧ).
Блок Digital Filter в схеме является петлевым фильтром. Петлевой фильтр представляет собой фильтр низких частот (ФНЧ), который подавляет сигнал на удвоенной частоте, в результате чего формируется управляющее напряжение.
При оценивании параметра задержки мы используем блок Discrete-Time VCO — генератор, управляемый напряжением. С его помощью генерируем сигнал, мгновенная частота которого меняется по закону, заданному отсчетами. Входные параметры блока следующие:
- Quiescent frequency (Hz) = fпч;
- Output amplitude =1 V;
- Input sensitivity (Hz/V) = 100;
- Initial phase = 0 rad;
- Sample time (s) = 1/ fнес.
Здесь fпч — промежуточная частота, fнес — частота несущей [3].
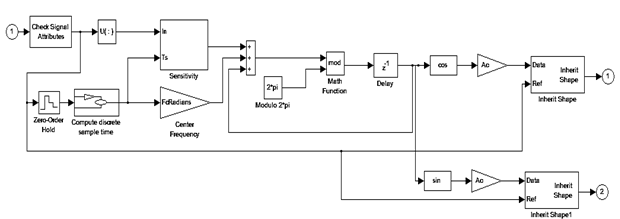
Рис. 6. Схема блока Discrete-Time VCO
На рисунке 7 мы видим показания осциллографа Scope, иллюстрирующие верную работу нашей схемы.

Рис. 8. Показания осциллографа Scope
По данным показателям мы можем оценить время задержки без обратной связи по решению для АМ в базовой полосе частот
В данной статье была проведена оценка параметра временной задержки, не управляемой решениями и реализована отслеживающая петля, оценивающая время сдвига без обратной связи по решению для АМ в базовой полосе частот. Смоделировав и описав данную схему, был показан принцип ее работы.
Литература:
1. Прокис Джон. Цифровая связь. Пер. с англ. / Под ред. Д. Д. Кловского. М.: Радио и связь. 2000. 800 с.
2. Шульгин В. И. Основы работы с Simulink Matlab, 2010. Режим доступа: http://k501.xai.edu.ua/lib/labrab_Shulgin_Osnovi %20raboti %20s %20SIMULINK %20MATLAB.pdf
3. Черных И. В. Моделирование электротехнических устройств в MATLAB, SimPowerSystems и Simulink. М.: ДМК Пресс, СПб.: Питер, 2008. 288 с.

