Мировые тенденции в области медицинского приборостроения в последние годы претерпели значительные изменения. В основном это вызвано необходимостью повышения качества диагностики, что приводит как к созданию новых высокоинформативных диагностических приборов, так и к совершенствованию традиционных технологий.
Под фильтрацией изображений понимают операцию, имеющую своим результатом изображение того же размера, полученное из исходного изображения по некоторым правилам. Обычно интенсивность (цвет) каждого пикселя результирующего изображения обусловлена интенсивностями (цветами) пикселей, расположенных в некоторой его окрестности в исходном изображении.
Изображения, подлежащие распознаванию, могут быть зашумлены. Причиной тому могут быть искажения, вносимые в изображение предметами, активно отражающими свет (стекло, железо, водные поверхности), неравномерная прозрачность воздушного слоя, пыль, попавшая в объектив, качество используемой аппаратуры и др. Поэтому необходима дополнительная предварительная фильтрации изображения.
В общем виде модель искаженного изображения имеет вид:
− в пространственном представлении: g(x,y)=h(x,y)⋅f(x,y)+ν(x,y){\displaystyle g(x,y)=h(x,y)\cdot f(x,y)+\nu (x,y)\,\!}
− в частотном представлении: G(u,v)=H(u,v)⋅F(u,v)+N(u,v){\displaystyle G(u,v)=H(u,v)\cdot F(u,v)+N(u,v)\,\!}
Если искажение представлено только шумом, то эти формулы принимают вид:
g(x,y)=f(x,y)+ν(x,y){\displaystyle g(x,y)=f(x,y)+\nu (x,y)\,\!}
или
G(u,v)=F(u,v)+N(u,v)
{\displaystyle G(u,v)=F(u,v)+N(u,v)\,\!}
Поскольку слагаемое, описывающее шум, неизвестно, то просто получить g(x,y){\displaystyle g(x,y)\,\!} или G(u,v){\displaystyle G(u,v)\,\!} невозможно. В таких случаях, когда присутствует только аддитивная составляющая шума, пространственная фильтрацияявляется лучшим (а в данном случае и единственным) решением.
Наиболее часто используемым фильтром является медианный фильтр. Обусловлено это двумя причинами:
Фильтры, основанные на порядковых статистиках, занимают промежуточное положение по соотношению скорость/качество среди всех прочих алгоритмов. К примеру, простейший фильтр, основанный на вычислении среднего, дает очень смазанное изображение, которое сложно впоследствии обрабатывать, а использование вейвлетов приводит к дополнительной параметризации программы, уменьшая тем самым степень автоматизма, а также замедлению работы, т. к. требует для вычисления дополнительных массивов данных.
Вейвлет-анализ является на сегодняшний день одной из самых перспективных технологий анализа данных.
Модель сигнала можно записать следующим образом:
s(t)=f(t)+σe(t)
{\displaystyle s(t)=f(t)+\sigma e(t)\,\!}
где f(t){\displaystyle f(t)\,\!} — полезный сигнал;
e(t){\displaystyle e(t)\,\!} — шум;
σ{\displaystyle \sigma \,\!} — уровень шума;
s(t){\displaystyle s(t)\,\!} — исследуемый сигнал.
Для такой модели удаление шума с помощью вейвлет-преобразования выполняется в 4 этапа:
− разложение сигнала по базису вейвлетов;
− выбор порогового значения шума для каждого из уровней разложения;
− пороговая фильтрация коэффициентов детализации;
− реконструкция сигнала.
Со статистической точки зрения такая методика представляет собой непараметрическую оценку модели сигнала с использованием ортогонального базиса. Методика наилучшим образом работает на достаточно гладких сигналах, т. е. на сигналах, в разложении которых лишь небольшое количество коэффициентов детализации значительно отличается от нуля.
Получаемые изображения, как правило, не настолько сильно зашумлены, что бы требовать очень тщательной фильтрации. Учитывая особенности применяемого при сегментации метода, достаточно просто удалить локальные выбросы яркости на изображении.
Пространственная фильтрация или окрестностная обработка изображений состоит из следующих действий:
- определение центральной точки (x, y) окрестности;
- совершение операции, которая использует лишь значения пикселей в заранее оговоренной окрестности вокруг центральной точки;
- назначение результата этой операции «откликом» совершаемого процесса в центральной точке окрестности;
- повторение всего процесса для каждой точки изображения. В результате перемещения центральной точки образуются новые окрестности, отвечающие каждому пикселю изображения.
Механизм линейной пространственной фильтрации проиллюстрирован на рисунке 1.
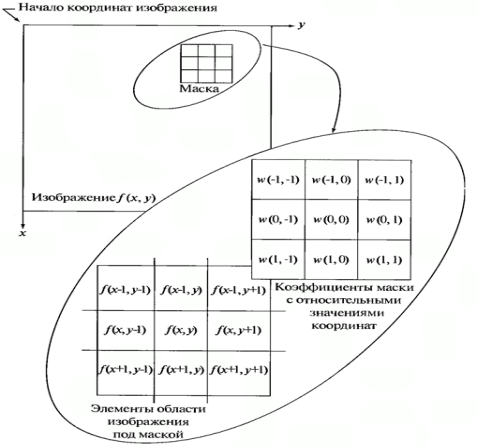
Рис. 1. Механизм линейной пространственной фильтрации
Процесс заключается в перемещении центра фильтрующей маски w от точки к точке изображения f. В каждой точке (х, у) откликом фильтра является сумма произведений коэффициентов фильтра и соответствующих пикселов окрестности, которые накрываются фильтрующей маской. Для маски размера m х n обычно предполагается, что и, где a и b — неотрицательные целые числа, т. е. основное внимание уделяется маскам, имеющим нечетные размеры, причем наименьшим содержательным размером маски считается размер 3x3 (маска 1x1 исключается как тривиальная). Преимущественное обращение с масками нечетных размеров является вполне обоснованным, поскольку в этом случае у маски имеется выраженная центральная точка.
Для получения более информативного изображения актуально использование различных видов его обработки, цифровых фильтров. Фильтры позволяют либо улучшить изображения, отсеяв ненужные «шумы» и мелкие частицы, либо изменить его так, чтобы акцентировать те или иные объекты на изображении.
Основные достоинства цифровых фильтров по сравнению с аналоговыми:
− цифровые фильтры могут иметь параметры, реализация которых невозможна в аналоговых фильтрах, например, линейную фазовую характеристику;
− цифровые фильтры не требуют периодического контроля и калибровки, т. к. их работоспособность не зависит от дестабилизирующих факторов внешней среды, например, температуры;
− один фильтр может обрабатывать несколько входных каналов или сигналов;
− входные и выходные данные можно сохранять для последующего использования.
Недостатками цифровых фильтров по сравнению с аналоговыми являются:
− трудность работы с высокочастотными сигналами. Полоса частот ограничена частотой Найквиста, равной половине частоты дискретизации сигнала. Поэтому для высокочастотных сигналов применяют аналоговые фильтры, либо, если на высоких частотах нет полезного сигнала, сначала подавляют высокочастотные составляющие с помощью аналогового фильтра нижних частот, затем обрабатывают сигнал цифровым фильтром;
− трудность работы в реальном времени — вычисления должны быть завершены в течение периода дискретизации;
− для большой точности и высокой скорости обработки сигналов требуется не только мощный процессор, но и дополнительное, аппаратное обеспечение в виде высокоточных и быстрых ЦАП и АЦП.
Сглаживающие фильтры применяются для расфокусировки изображения и подавления шума. Расфокусировка может применяться как предварительный шаг обработки изображения, например, для удаления мелких деталей перед обнаружением больших объектов. Для подавления шумов может использоваться расфокусировка с применением как линейной, так и нелинейной фильтрации.
С помощью пространственного цифрового фильтра были обработаны реальные фиброскопические изображения. Были использованы два фильтра: фильтр высоких частот и фильтр низких частот.
При низкочастотной фильтрации расфокусировка изображения, позволяющая создать грубый образ объектов, которые могут представлять интерес. При этом интенсивность мелких объектов смешивается с фоном, в то время как большие объекты остаются в виде пятен и могут быть легко обнаружены (рисунок 2б).
При высокочастотной фильтрации заметно повышение четкости границ и усиление других контуров. Вместе с тем высокочастотная фильтрация гасит низкие частоты и отфильтрованное изображение теряет большую часть фоновой тональности, имевшуюся на исходном изображении (рисунок 2в).
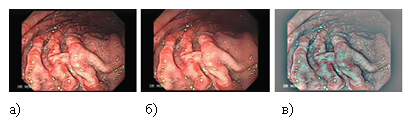
Рис. 2. Фильтрация изображения: а) — исходное изображение, б) — низкочастотная фильтрация, в) — высокочастотная фильтрация
Фильтрация изображений в настоящее время способна упростить работу врача, ускорив процесс выявления патологий и снизив риск постановки неверного диагноза.
Как показывает практика, при применении фильтрации возможно значительное улучшение изображения — повышение резкости, снижение уровня шумов и т. п. Кроме того, фильтрация — универсальное средство для повышения качества изображения. Следовательно, фильтрацию рекомендуется использовать в дальнейшем для обработки изображений с целью их последующего улучшения.
Литература:
- Дмитриев А. Л. Оптические методы обработки информации. — СПб.: СПбГУИТМО, 2005. — 46 с.
- Куликов А. Ю. Волоконно-оптическая система формирования изображений. — Радиосистемы. — Тамбов: 2003. — 41–44 с.
- Чео П. К. Волоконная оптика: приборы и системы. — Энергоатомиздат. — 1991. — 324 с.
- Иванов Д. В. Алгоритмические основы растровой графики. — М.: Учебное пособие, 2007. — 166 с.

