Распознавание образов — научная дисциплина, целью которой является выявление объектов по нескольким критериям или классам. Теория распознавания объектов представляет собой раздел информатики, который основывается на разработке основ и методов идентификации предметов, явлений и сигналов. Потребность в таком распознавании возникает во многих областях, начиная с машинного зрения, символьного распознавания, диагностики в медицине, распознавания речи и заканчивая узко специальными задачами. Несмотря на то, что некоторые из этих задач решаются человеком на подсознательном уровне с большой скоростью, до настоящего времени ещё не создано компьютерных программ, решающих их в столь же общем виде [1,2]. В связи с этим, проблема распознавания образов получила повсеместное распространение, в том числе в области искусственного интеллекта и робототехники.
Возможность распознавания базируется на схожести подобных объектов. Несмотря на то, что все явления и предметы не похожи друг на друга, между некоторыми из них всегда можно найти сходства по тому или иному признаку
Все методы распознавания объектов делятся на два вида: методы, основанные на теории решений и структурные методы. Первые основаны на вычислении с помощью количественных величин, таких как длина, текстура и т.д. Вторые ориентированы на образы, для описания которых больше подходят качественные величины, например реляционные. Также в распознавании объектов немаловажную роль играет обучение на основе известной выборки.
Под образом подразумевается некоторая упорядоченная совокупность признаков. Классом образов называется совокупность объектов с одинаковыми свойствами. Классификатором или решающим правилом называется правило отнесения образа к одному из классов на основании его вектора признаков. На практике широкое применение имеют три формы представления признаков: вектор признаков (для количественных величин), символьная строка и деревья признаков (для структурных величин) [3].
Методы, основанные на сопоставлении, представляют собой наборы векторов признаков каждого класса объектов. Новый образ будет отнесен к тому классу, который окажется наиболее близким, в пределах заранее заданной метрики. Очевидно, что самый простой подход состоит в поиске минимального расстояния, которое вычисляется при помощи евклидовых норм между векторами признаков неизвестного объекта и векторами прототипа. Вывод о принадлежности объекта к определенному классу происходит по наименьшему из этих расстояний. Минимальный классификатор расстояния хорошо работает в тех случаях, где расстояние между точками математического ожидания классов велико по сравнению с диапазоном разброса объектов каждого класса.
Не менее важными являются методы распознавания образов, основанные на вероятностных классификаторах, по причине случайностей, которые влияют на порождение классов образов. Следовательно, необходимо выработать такой оптимальный подход, при использовании которого окажется наименьшая вероятность появления ошибок.
Очень сложно однозначно ответить, как выглядит оптимальный метод описывающий компьютерное зрение. Однако, можно разделить все существующие методы на три ступени: первичная обработка и фильтрация, логическая оценка результатов фильтрации и алгоритмы принятия решений [2]. Как правило, для распознавания объектов на изображении необходимо применить все эти этапы, однако бывает достаточно двух, или даже одного.
К группе фильтрации можно отнести методы, которые позволяют определить на изображении интересующие объекты, без предварительного анализа. Основная масса таких методов использует какую-либо единую операцию ко всем точкам изображения одновременно. На данном уровне анализ как правило не проводится.
Самым простым преобразованием является бинаризация изображения по порогу. Для изображений 
и в градациях серого таким порогом является значение яркости. Выбор порога, определяющего бинаризацию, определяет вид самого процесса. Как правило, бинаризация происходит при алгоритме аддитивного выбора порога. Например, таким алгоритмом может стать выбор математического ожидания или моды, а также наибольшего пика гистограммы.
Существующие классические методы фильтрации могут быть применены в широком спектре задач. Наиболее распространенным классическим методом является преобразование Фурье, однако он не используется в изображениях в чистом виде [3,4]. Однако для анализа изображений часто бывает недостаточно простого одномерного преобразования, и требуется гораздо более ресурсоемкое двумерное преобразование:
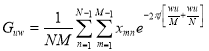
Вычисление по такой формуле является достаточно трудоемким, поэтому на практике чаще пользуются сверткой интересующей области с помощью низкочастотных или высокочастотных фильтров, в зависимости от конкретной задачи. Такое упрощение конечно, не позволяет более широкого диапазона операций, таких как анализ, однако зачастую бывает достаточно только результата без последующих преобразований.
Вейвлет-преобразования являются более перспективным и современным методом обработки изображений, чем преобразование Фурье [5]. Они упрощают сжатие, анализ и передачу большого количества изображений. Вейвлет-преобразования основаны на разложения по малым волнам (вейвлетам) с изменяющейся частотой и ограничением по времени, в отличие от преобразования Фурье, построенного на гармонических функциях.
В 1987 году Стефан Маллат впервые продемонстрировал, что вейвлеты могут быть положены в основу принципиально нового метода обработки изображений, получившего название кратномасштабный анализ. Как очевидно из названия, кратномасштабная теория имеет дело с анализом изображений при различных разрешениях, так как многие детали, незаметные при одном масштабе, могут быть легко найдены при другом. Долгое время вейвлеты обладали весьма ограниченным распространением, однако в настоящий момент уже трудно уследить за всей информацией, имеющейся по этой теме.
При взгляде на изображение, мы видим связанные наборы объектов одинаковой яркости и структуры, которые объединяясь образуют предметы или области отображения. Когда присутствуют одновременно, как маленькие объекты, так и большие, то анализ изображения в разных разрешениях позволит значительно расширить области обработки.
С математической точки зрения изображение является двумерной матрицей значений яркости. Однако при переходе от одной его части к другой, даже такие статистики первого порядка, как гистограммы значительно меняются. Существует набор классических функций, применяемых в вейвлет преобразованиях [5]: вейвлет Хаара, вейвлет Морле, вейвлет Добеши и т.д. Хорошим примером применения вейвлет анализа является задача поиска блика в зрачке глаза, где вейвлетом является сам блик.
В основе вейвлетов лежит корреляция, которая может применяться как в совокупности с другими методами, так и самостоятельно. При распознавании образа в изображении это незаменимый инструмент.
Другим не менее интересным классом фильтрации является фильтрация функций. Она позволяет на простом изображении найти множество кусочков простейших функций (прямая, парабола и т.д.). Наиболее известным является преобразование Хафа, которое позволяет находить любые эффективно вычислимые функции. Его аналогом является преобразование Радона, которое за счет вычисления через быстрое преобразование Фурье дает выигрыш в производительности.
Отдельный раздел фильтрации — фильтрация контуров. Она очень полезна в той ситуации, когда объект достаточно сложный, но имеет четкие границы. Тогда фильтрация контуров является чуть ли не одним из основных инструментов работы с изображением и проводится с использованием операторов Кенни, Лапласа, Прюитта, Собеля и Робертса.
Рассмотренные фильтры могут решить большинство задач, однако не стоит забывать о менее распространенных, но используемых в локальных задачах [6]: итерационные фильтры, курвлет и бамблет преобразования и т.д.
Поле фильтрации на выходе получается набор данных поддающихся обработке. Но порой они все же требуют дополнительных логических преобразований. Поэтому необходимо введение методов, позволяющих перейти от целого изображения к свойствам объектов на нем.
Методы математической морфологии являются средством перехода от фильтрации к логике. Они позволяют убрать шумы на бинарном изображении, изменив размер имеющихся элементов. Также существует множество методов, которые позволяют идентифицировать объект по контуру. Такой подход называется контурным анализом. Особые точки являются уникальными характеристиками которые позволяют сопоставить разные классы объектов. Существует три вида особых точек: особые точки, являющиеся стабильными на протяжении времени; особые точки, являющиеся при смене освещения и небольших движениях объекта; и стабильные особые точки.
Методы машинного обучения и принятия решений являются финальной стадией в распознавании образов. Они находятся на стыке математической статистики, методов оптимизации и классических математических дисциплин, но имеет также и собственную специфику, связанную с проблемами вычислительной эффективности и переобучения. В большинстве случаев суть обучения заключается в следующем: на основе обучающей выборки с признаками каждого класса построить такую модель, с помощью которой машина сможет проанализировать новое изображение и решить, какой из объектов имеется на изображении. Существует два типа обучения: на основе человеческий знаний, перенесенных в компьютер в виде базы и обучение по прецедентам (индуктивное) основанное на выявлении закономерностей. В реальных прикладных задачах входные данные об объектах могут быть неполными, неточными, нечисловыми, разнородными. Эти особенности приводят к большому разнообразию методов машинного обучения.
Таким образом, мы провели краткий анализ существующих методов машинного распознавания образов. Искусственный интеллект и некоторые смежные области, такие как анализ сцен и машинное зрение, все еще пребывают на начальных стадиях развития. Однако, описанные подходы действительно крайне разнообразны и с помощью большинства из них можно решить практически любую задачу распознавания образов.
Литература:
- Вудс Р., Гонсалес Р. Цифровая обработка изображений //М.: Техносфера. — 2005.
- Гонсалес Р., Вудс Р., Эддинс С. Цифровая обработка изображений в среде MATLAB //М.: Техносфера. — 2006. — Т. 616. — С. 6.
- Дж Т., Гонсалес Р. Принципы распознавания образов. — 1978.
- Вапник В. Н., Червоненкис А. Я. Теория распознавания образов. Статистические проблемы обучения. — 1974.
- Дремин И. М., Иванов О. В., Нечитайло В. А. Вейвлеты и их использование //Успехи физических наук. — 2001. — Т. 171. — № . 5. — С. 465-501.
- Шапиро Л., Стокман Д. Компьютерное зрение //М.: Бином. Лаборатория знаний. — 2006. — Т. 752.
