Ключевые слова:вероятностный алгоритм, простые числа, псевдопростые числа, слабо псевдопростые числа, эффективность теста.
Введение
С развитием возможностей вычислительной техники в криптографии и возникновением в 1976 году идеологии открытого ключа, начали активно использовать фундаментальные результаты теории чисел и современной алгебры. В них на первый план выходит порядок цифр, с которыми приходится работать. Такие числа должны быть достаточно большими, чтобы обеспечивать крипто-аналитическую устойчивость алгоритма, который используется. В то же время, их нужно генерировать сравнительно быстро. Это обусловливает важность построения эффективных алгоритмов для проверки большого случайного числа на простоту (случайность выбранного числа так же важна для обеспечения устойчивости). Все такие алгоритмы можно разделить на две группы: детерминированные и вероятностные. Первые устанавливают простоту числа математически строго, и, как правило, требуют много времени для проверки, в то время как другие просто минимизируют вероятность погрешности в определении простоты после каждого последовательного своего запуска.
Постановка задачи.
Сформулируем основные направления поиска больших простых чисел.
1. Для заданного большого натурального числа  выяснить, является ли оно простым. Можно последовательно перебирать простые числа меньше заданного числа (точнее меньше
выяснить, является ли оно простым. Можно последовательно перебирать простые числа меньше заданного числа (точнее меньше 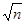 ), чтобы найти все его делители. Тогда приобретает актуальность не столько время работы алгоритма, как его асимптотическое поведение при росте количества цифр числа
), чтобы найти все его делители. Тогда приобретает актуальность не столько время работы алгоритма, как его асимптотическое поведение при росте количества цифр числа  .
.
2. Найти большое простое число. Самые большие простые числа, найденные на сегодня, имеют специальный вид. Для чисел специального вида разработаны алгоритмы проверки на простоту, которые невозможно применить к обычным числам. Такие числа нельзя считать случайными, и они почти не применяются в асимметрических криптосистемах. Например, числа Мерсенна, это числа вида 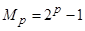 . В начале февраля 2013 математик Кертис Купер, участник проекта вычислений GIMPS (Great Internet Mersenne Prime Search), нашел сорок восьмое простое число Мерсенна, десятичная запись которого имеет 17 425 170 знаков.
. В начале февраля 2013 математик Кертис Купер, участник проекта вычислений GIMPS (Great Internet Mersenne Prime Search), нашел сорок восьмое простое число Мерсенна, десятичная запись которого имеет 17 425 170 знаков.
3. Найти большое случайное простое число. В этом случае мы тестируем различные случайные числа заданной сложности (под сложностью имеем в виду количество знаков в бинарной записи числа), пока не встретим простое.
4. Найти простое число, которое будет делителем заданного натурального числа (разложить заданное натуральное число на множители). Эта задача часто возникает в криптоанализе, и в некотором смысле служит обобщением первой проблемы — ведь если нам не удалось найти ни одного собственного делителя числа 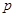 — это и означает, что оно простое. На самом деле, разложить число на множители сложнее, чем проверить его на простоту — существование полиномиального алгоритма для разложения числа на множители не доказано.
— это и означает, что оно простое. На самом деле, разложить число на множители сложнее, чем проверить его на простоту — существование полиномиального алгоритма для разложения числа на множители не доказано.
В этой работе рассматривается первая проблема — проверка простоты большого числа.
Формализация задачи.
Дано натуральное число 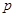 . Установить, является ли оно простым с помощью некоторого алгоритма. Важнейшим критерием качества нашего алгоритма будет время его выполнения. Это время можно существенно уменьшить, если использовать вероятностные методы проверки. Вероятностные тесты работают намного быстрее детерминированных, но имеют определенный недостаток. После положительного прохождения числом теста, остается вероятность того, что оно на самом деле составное.
. Установить, является ли оно простым с помощью некоторого алгоритма. Важнейшим критерием качества нашего алгоритма будет время его выполнения. Это время можно существенно уменьшить, если использовать вероятностные методы проверки. Вероятностные тесты работают намного быстрее детерминированных, но имеют определенный недостаток. После положительного прохождения числом теста, остается вероятность того, что оно на самом деле составное.
Требования к вероятностному алгоритму проверки простоты.
1. С самого начала мы считаем, что число простое, а с помощью алгоритма попробуем установить, является ли оно составным (установить непростоту числа значительно легче, чем простоту).
2. Алгоритм устанавливая простоту числа может ошибиться, а именно — составное число определяет как простое.
3. Алгоритм зависит от параметра, который выбирается каждый раз случайным образом. Мы можем применять алгоритм много раз с разными значениями параметра, и с каждым его последующим применением, вероятность того, что исследуемое число является составным, должна уменьшаться.
4. После того как параметр пробегает все заранее определенное параметрическое множество, наш вероятностный алгоритм превращается в детерминированный.
Алгоритм частичного деления.
Можно рассматривать алгоритм частичного деления как вероятностный тест. Пусть нам надо проверить простоту числа  . Мы проверяем, не делится ли оно на какое-то из чисел
. Мы проверяем, не делится ли оно на какое-то из чисел 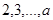 . В этом случае
. В этом случае 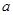 является параметром, а параметрическим множеством будет
является параметром, а параметрическим множеством будет 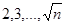 . Когда
. Когда 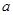 пробегает все множество параметров, то тест становится детерминированным. Но в этом случае, вряд ли можно говорить об эффективности этого теста, если мы планируем проверять с его помощью очень большие числа.
пробегает все множество параметров, то тест становится детерминированным. Но в этом случае, вряд ли можно говорить об эффективности этого теста, если мы планируем проверять с его помощью очень большие числа.
Но перед проверкой данного числа на простоту с помощью малой теоремы Ферма и других методов, целесообразно провести базовое исследование на наличие малых простых делителей. Это позволяет существенно сократить время поиска простого числа, в случае, когда нас интересует нахождение хотя бы одного такого числа (эта проблема возникает в кратковременных процедурах шифрования, когда время при кодировании-декодирования для нас играет большую роль, чем время, которое требуется для криптоанализа).
Алгоритм базового метода может быть представлен следующими шагами:
1. Задаем 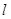 — нижнюю границу диапазона, в котором должно находиться простое число.
— нижнюю границу диапазона, в котором должно находиться простое число.
2. Задаем 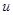 — верхнюю границу диапазона, в котором должно находиться простое число.
— верхнюю границу диапазона, в котором должно находиться простое число.
3. Проверяемо корректность задания диапазона 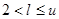 .
.
4. Подсчитываем максимальное количество попыток 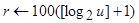 .
.
5. 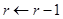 .
.
6. Если 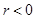 , то лимит попыток исчерпан (событие очень мало вероятно, и на практике практически никогда не встречается. В том случае, когда это все же случилось, нужно просто перезапустить тест).
, то лимит попыток исчерпан (событие очень мало вероятно, и на практике практически никогда не встречается. В том случае, когда это все же случилось, нужно просто перезапустить тест).
7. Выбираем в заданном интервале 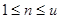 случайное число
случайное число  .
.
8. Если  меньше чем 2000, то тестирование выполняется методом пробного деления на все известные простые числа, которые меньше чем
меньше чем 2000, то тестирование выполняется методом пробного деления на все известные простые числа, которые меньше чем  .
.
9. Если  больше чем 2000, то тестирование выполняется методом пробного деления на все простые числа, меньше чем 2000. Если делитель существует, то переходим к шагу 5.
больше чем 2000, то тестирование выполняется методом пробного деления на все простые числа, меньше чем 2000. Если делитель существует, то переходим к шагу 5.
10. На этом шаге можно приступать к проверке числа  на простоту другим методом (который не связан с методом частичного деления).
на простоту другим методом (который не связан с методом частичного деления).
11. Если результат теста отрицательный ( оказалось составным), переходим к шагу 5.
оказалось составным), переходим к шагу 5.
12. Если результат тест положительный, то мы генерируем простое число, что нам и было нужно.
Ключевым в этом тесте является пункт 9. Он позволяет отбросить 85 % чисел перед запуском выбранного нами алгоритма для исследования простоты.
Следует отметить, что эффективность частичного деления никак не зависит от основного алгоритма (который запускается на 10 шаге). Очевидна целесообразность использования частичного деления.
Псевдопростые числа.
Псевдопростым числом называют составное натуральное число, которое имеет некоторые свойства простых чисел. Существование псевдопростых чисел препятствует работе алгоритмов, которые используют те или иные свойства простых чисел.
Согласно малой теореме Ферма для любого простого числа 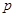 и для произвольного натурального числа
и для произвольного натурального числа  взаимнопростого с
взаимнопростого с 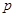 , имеет место сравнение:
, имеет место сравнение:
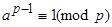 (1)
(1)
На основе этой теоремы можно построить достаточно мощный тест на простоту.
Тест Ферма.
Для 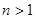 выбираем
выбираем 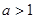 , и вычисляем
, и вычисляем 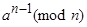 , если результат не равен 1, то
, если результат не равен 1, то  составное, если 1, то
составное, если 1, то — псевдопростое по основанию
— псевдопростое по основанию 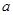 или псевдопростое число Ферма.
или псевдопростое число Ферма.
Некоторые составные числа являются псевдопростыми по любым основаниям. Это так называемые абсолютно псевдопростые числа, их еще называют числами Кармайкла. Ситуация, когда исследуемое число окажется совершенно псевдопростым, очень мало вероятна, но формально мы не можем ее опускать.
Эффективность теста Ферма для слабо псевдопростых чисел.
Исследуем насколько эффективен тест Ферма для чисел, которые не являются числами Кармайкла. Такие числа будем называть слабо псевдопростыми.
Обозначим через 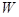 множество всех значений параметра
множество всех значений параметра 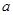 , для которых
, для которых  проходит тест Ферма на простоту, а именно
проходит тест Ферма на простоту, а именно
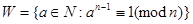 (2)
(2)
Поскольку, по нашему предположению,  не является абсолютно псевдопростым, то
не является абсолютно псевдопростым, то 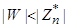 , т. е.
, т. е. 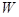 не может совпадать со всей мультипликативной группой
не может совпадать со всей мультипликативной группой 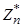 вычетов, взаимнопростых с
вычетов, взаимнопростых с  . Легко понять, что
. Легко понять, что 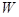 — подгруппа группы
— подгруппа группы 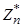 , поэтому
, поэтому 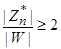 . Это означает, что среди элементов параметрического множества нашего вероятностного теста, максимум половина из них может привести к продолжению прогонки (все вычеты с
. Это означает, что среди элементов параметрического множества нашего вероятностного теста, максимум половина из них может привести к продолжению прогонки (все вычеты с 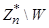 сразу покажут, что
сразу покажут, что  не является простым). Отсюда следует, что после
не является простым). Отсюда следует, что после 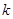 прогонок теста Ферма для слабо псевдопростого числа, вероятность погрешности в определении простоты числа
прогонок теста Ферма для слабо псевдопростого числа, вероятность погрешности в определении простоты числа  составит не более
составит не более 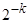 (конечно же, при условии случайного выбора вычетов из параметрического множества).
(конечно же, при условии случайного выбора вычетов из параметрического множества).
Таким образом, тест Ферма будет эффективным для чисел, которые не являются абсолютно псевдопростыми — мы можем с большой точностью устанавливать простоту таких чисел. Проблема лишь в том, что следует сначала отсеять числа Кармайкла, а это почти нереально для тех порядков чисел, которые сейчас применяются в криптографических протоколах.
Тест Соловея-Штрассена.
Рассмотрим тест, который строится на обобщении малой теоремы Ферма. Используем критерий Эйлера.
Утверждение 1. Для произвольного нечетного  следующие условия эквивалентны:
следующие условия эквивалентны:
1.  — простое;
— простое;
2. для произвольного 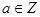 выполняется сравнение:
выполняется сравнение:
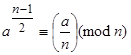 ,
, 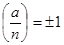 . (3)
. (3)
Этот критерий позволяет нам использовать следующий вероятностный тест.
1. Выбираем 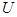 — коэффициент точности (чем больше этот коэффициент, тем выше точность установки простоты
— коэффициент точности (чем больше этот коэффициент, тем выше точность установки простоты  ).
).
2. 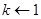 .
.
3. Выбираем из упорядоченного по величине массива простых чисел 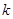 — непростое число.
— непростое число.
4. Проверяем, выполняется ли сравнение (3).
5. Если сравнение не выполняется, то ответ « — составное».
— составное».
6. Если сравнение выполняется, то 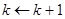 .
.
7. Если 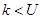 , то переходим к третьему шагу.
, то переходим к третьему шагу.
8. Если 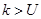 , то ответ: «
, то ответ: « — псевдопростое с вероятностью
— псевдопростое с вероятностью 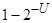 ».
».
Легко видеть, что этот тест удовлетворяет требованиям эффективного вероятностного теста на простоту: множеством параметров выступают простые числа, меньше 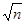 , и после каждого прогона теста вероятность того, что простота числа определена неправильно, уменьшается вдвое. При этом тест Соловея-Штрассена лишен главного недостатка теста Ферма — для всех натуральных
, и после каждого прогона теста вероятность того, что простота числа определена неправильно, уменьшается вдвое. При этом тест Соловея-Штрассена лишен главного недостатка теста Ферма — для всех натуральных  многократная прогонка теста уменьшает вероятность ошибки до нуля.
многократная прогонка теста уменьшает вероятность ошибки до нуля.
Следует также отметить главный недостаток теста Соловея-Штрассена — это время его выполнения. Если возведение в степень по модулю можно осуществить за сравнительно малое время, то про вычисление символа Лежандра этого сказать нельзя. Проблема осложняется необходимостью проводить тест несколько раз — при этом уменьшение вероятности ошибки мы считаем приемлемой.
Формализуем задачу. Пусть для нас приемлема вероятность погрешности 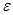 . Для ее обеспечения нам достаточно
. Для ее обеспечения нам достаточно 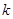 прогонок теста, где
прогонок теста, где 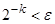 . Мы можем существенно уменьшить время, необходимое для обеспечения достаточной точности определения простоты, если улучшим оценку
. Мы можем существенно уменьшить время, необходимое для обеспечения достаточной точности определения простоты, если улучшим оценку 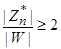 , заменив двойку на какое-то большее число.
, заменив двойку на какое-то большее число.
Видим, что слишком большое количество прогонок теста Соловея-Штрассена, необходимое для достижения приемлемой точности оценки простоты больших натуральных чисел, делает его практически не применимым. Однако тест допускает модификации, которые позволяют оптимизировать количество его последовательных применений для достижения заданной точности. Дальнейшая оптимизация теста Соловея-Штрассена реализована в вероятностных тестам Леманна, Миллера-Рабина. Эти тесты подробно рассмотрены в [4].
Оценки скорости алгоритмов.
Приведем эмпирические оценки скорости алгоритмов (количество операций, необходимых для проведения одного цикла теста), описанных в этой работе. Такие оценки чаще всего предоставляются в виде некоторой функции от числа проверяемого и содержат в себе некоторые константы, численное значение которых для нас неважно — ведь имеет значение лишь асимптотика этой функции при увеличении порядка исследуемого числа. Доказательство этих оценок не приводится, поскольку оно опирается на некоторые нетривиальные факты теории алгоритмов. Подробно методы получения оценок такого рода описаны в книге [6].
1. Для теста на основе частичного деления, количество операций для полной проверки числа  на простоту не превышает
на простоту не превышает 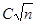 для некоторой константы
для некоторой константы 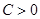 . Эта оценка следует из того, что для каждого частичного деления необходимо лишь конечное число операций (для нас нужно, чтобы она не зависела от
. Эта оценка следует из того, что для каждого частичного деления необходимо лишь конечное число операций (для нас нужно, чтобы она не зависела от  ). На практике, уже для чисел порядка 1030 получаем такое количество операций, которое не способен выполнить за приемлемое время мощный компьютер. Для вероятностной модификации теста частичного деления время зависит от мощности параметрического множества, которое обеспечивает заданную точность проверки простоты. В рассматриваемом нами примере это множество имеет мощность
). На практике, уже для чисел порядка 1030 получаем такое количество операций, которое не способен выполнить за приемлемое время мощный компьютер. Для вероятностной модификации теста частичного деления время зависит от мощности параметрического множества, которое обеспечивает заданную точность проверки простоты. В рассматриваемом нами примере это множество имеет мощность 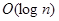 .
.
2. Для тестов Ферма и Соловея-Штрассена количество операций оценивается числом 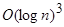 , то есть полиномиальной функцией от количества знаков числа
, то есть полиномиальной функцией от количества знаков числа  . Необходимость запускать эти тесты большое количество раз увеличивает эту оценку до
. Необходимость запускать эти тесты большое количество раз увеличивает эту оценку до 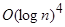 — в соответствии с мощностью параметрического множества.
— в соответствии с мощностью параметрического множества.
В то же время, быстрые детерминированные тесты показывают значительно худшие результаты. Полиномиальный алгоритм, предложенный Агравалом, Кайялом и Саксен, дает результат 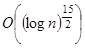 [2].
[2].
Выводы. Исследование алгоритмических проблем теории чисел, является актуальным с момента изобретения первых криптосистем с открытым ключом. Причем важно как совершенствование самих криптографических алгоритмов и методов генерации простых чисел, так и исследования устойчивости этих алгоритмов с точки зрения криптоанализа. Использование вероятностных тестов дает нам существенный выигрыш в скорости. Значение погрешности при установлении простоты числа, получаемого уже после небольшого количества прогонок тестов, может удовлетворить даже требовательного криптографа.
Литература:
1. Alford, W.R.; Granville, A.; Pomerance, C. There are Infinitely Many Carmichael Numbers // Annals of Mathematics. — 1994. — № 139. — P. 703–722.
2. Agrawal, M.; Kayal, N.; Saxena, N. Primes is in P // Annals of Mathematics. –2004. –№ 160. — P. 781–793.
3. Василенко О. Н. Современные способы проверки простоты чисел // Кибернетический сборник. — 1988. — № 25. — С. 162–187.
4. Василенко О. Н. Теоретико-числовые алгоритмы в криптографии. — М.:МЦНМО, 2006. — 336 с.
5. Коблиц Н. Курс теории чисел в криптографии. — М.: Научное изд-во: ТВП, 2001. — 254 с.
6. Черемушкин А. В. Лекции по арифметическим алгоритмам в криптографии. — М.:МЦНМО, 2002. — 104 с.

