Известно, что для обеспечения фокусировки электронного потока в лампах бегущей волны (ЛБВ) применяются магнитные периодические фокусирующие системы (МПФС) различных видов [1]:
1) моногармонические МПФС (рис. 1а);
2) полигармонические МПФС (рис. 1б);
3) реверсивные МРФС (рис. 1в).
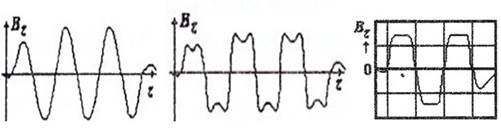
а) б) в)
Рис. 1. Продольное распределение магнитного поля в магнитных периодических фокусирующих системах (МПФС)
Моделирование вышеперечисленных видов МПФС разделено два основных этапа (рис. 2) [1–4]:
- моделирование продольного распределения магнитного поля ячейки МПФС (отдельного магнита);
- моделирование продольного распределения магнитного поля МПФС, которое реализуется с использованием реального механизма формирования распределения [5].
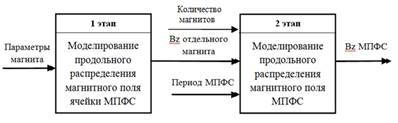
Рис. 2. Два этапа моделирования продольного распределения магнитного поля всех видов МПФС
В статье [2] рассмотрена программа для моделирования продольного распределения магнитного поля МРФС в среде MATHCAD. Для построения математической модели продольного распределения магнитного поля ячейки МРФС принята графическая модель (рис. 3), которая представляет собой кусочно-линейную функцию, определяемую точками A — H, и рассматривается как модернизированная вейвлет-функция «Французская шляпа».
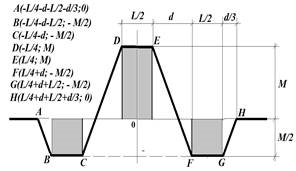
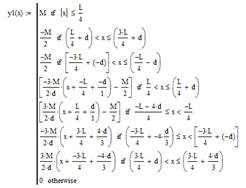
а) б)
Рис. 3. Графическая модель (а) и математическая модель продольного распределения магнитного поля ячейки МРФС [4]
Известно, что продольное распределение магнитного поля МРФС представляет собой совокупность чередующихся продольных распределений магнитных полей составляющих ее ячеек (магнитов), разнесенных по вертикальной оси на расстояние друг от друга, равное периоду МРФС [4]. Используя реальный механизм формирования МПФС [5] с периодом равным (L/2+d) для математических моделей магнитов (рис. 3б) и обратной ей функции получим продольное распределение магнитного поля МРФС, состоящее из 6 магнитов (рис. 4).
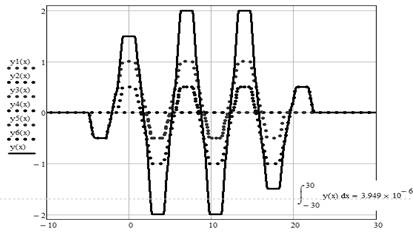
Рис. 4. Продольное распределение магнитного поля МРФС (сплошная линия), состоящее из 6 чередующихся магнитов при М=1, L=2, d=3
Для моделирования создана программа расчета продольного распределения магнитного поля МРФС в среде MAthcad [2], листинг которой приведен на рис. 5.
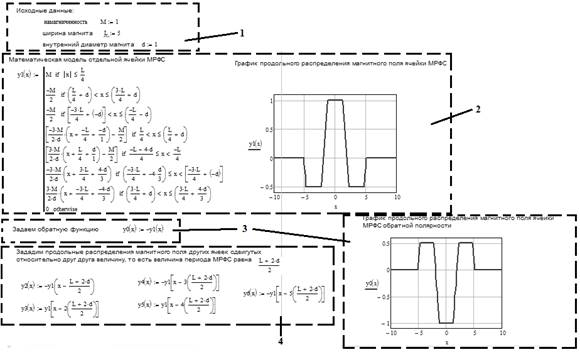
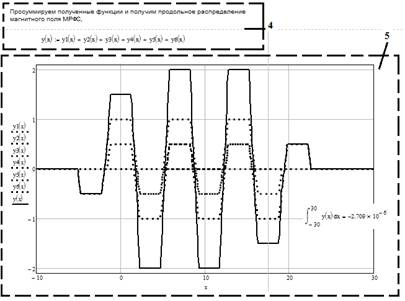
Рис. 5. Листинг программы расчета продольного распределения магнитного поля МРФС с заданными значениями M, L и d (среда MathCad)
Программа расчета для удобства (рис. 5) разделена на блоки: 1 — исходные данные (входные параметры модели ячейки МРФС), 2 — математическая модель ячейки МРФС (1), 3 — получение обратной функции; 4 — математическая модель МРФС, где задается количество ячеек (магнитов) и период МРФС (L/2+d), 5 — область визуализации результатов моделирования. Последовательность блоков 1–5 определяет алгоритм программы моделирования [2].
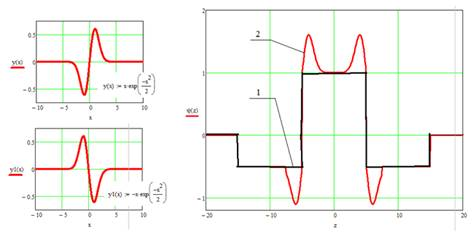
Рассмотрим еще один вид продольного распределения магнитного поля МРФС [3], формирование суммирующего распределения, которого происходит путем наложения на вейвлет — функцию «Французская шляпа» (рис. 6б, линия 1) двух вейвлет — функций Гаусса первого порядка (рис. 6а), при этом последние разрываются в точке перегиба и сдвигаются в начало «горизонтальных» площадок первой вейвлет — функции.
а) б)
Рис. 6. Суммирующее распределение (б, линия 2), состоящее из вейвлет-функции «Французская шляпа» (б, линия 1) и двух вейвлет — функций Гаусса первого порядка (а)
Заменим вейвлет-функцию «Французская шляпа» модернизированной вейвлет-функцией «Французская шляпа» [4], добавив вейвлет-функции Гаусса первого порядка (рис.6), и получим продольное распределение магнитного поля МРФС (рис. 7) [3].
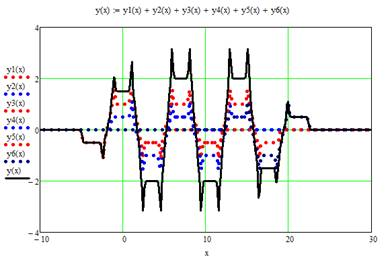
Рис. 7. Продольное распределение МРФС из 6 магнитов при следующих параметрах М=1, L=5, d=1 с коэффициентом сжатия для вейвлет-функции Гаусса первого порядка k=7
Для моделирования данного распределения создадим программу расчета продольного распределения магнитного поля МРФС в среде MAthcad [2], листинг которой приведен на рис. 8. Ее аналогично можно разбить на блоки, как показано на рис. 5.

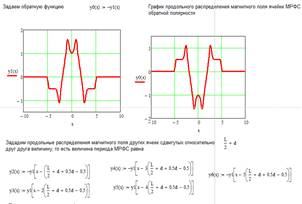
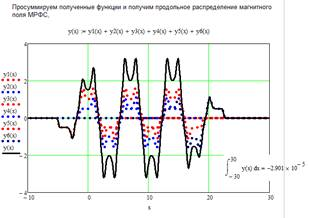
Рис. 8. Листинг программы расчета продольного распределения магнитного поля МРФС с заданными значениями M, L и d(среда MathCad) (рис. 6б)
Сравнение листингов программ на рис. 5 и рис. 8 показывает, что алгоритм вычисления одинаков, а отличием является только математическая модель распределения ячейки МРФС (отдельного магнита). Это позволяет в перспективе создать пользовательское приложение, в котором необходимо выбирать математическую модель распределения и задать параметры отдельного магнита для решения задачи моделирования распределения МРФС.
Литература:
1. Кожанова Е. Р. Автоматизация моделирования продольного распределения магнитного поля полигармонических магнитных периодических фокусирующих систем в среде MATHCAD // материалы II Международной научной конференции «Технические науки: проблемы и перспективы». СПб.: Заневская площадь, 2014. С. 112–116.
2. Кожанова Е. Р. Программа для моделирования продольного распределения магнитного поля магнитной реверсивной фокусирующей системы в среде MATHCAD // Новый университет. Серия: Технические науки. 2014. № 1 (23). С. 20–24.
3. Кожанова Е. Р., Захаров А. А., Ткаченко И. М. Возможность применения вейвлет-функции Гаусса первого порядка для моделирования продольного распределения магнитного поля реверсивных магнитных периодических систем // Молодой ученый. 2014. № 2 (61). С. 149–152.
4. Кожанова Е. Р., Захаров А. А. Применение модернизированной вейвлет-функции «Французская шляпа» для аппроксимации продольного распределения магнитного поля в магнитных реверсивных фокусирующих системах // Молодой ученый. 2012. № 9. С. 25–29.
5. Кожанова Е. Р., Захаров А. А. Формирование распределения суммирующих вейвлет-функций для моделирования продольного распределения магнитного поля магнитных периодических фокусирующих систем // Вестник Саратовского государственного технического университета. 2011. Т.4. № 1. С. 83–88.







