Автоматизация моделирования продольного распределения магнитного поля полигармонических магнитных периодических фокусирующих систем в среде Mathcad
Автор: Кожанова Евгения Романовна
Рубрика: 14. Общие вопросы технических наук
Опубликовано в
Дата публикации: 01.04.2014
Статья просмотрена: 72 раза
Библиографическое описание:
Кожанова, Е. Р. Автоматизация моделирования продольного распределения магнитного поля полигармонических магнитных периодических фокусирующих систем в среде Mathcad / Е. Р. Кожанова. — Текст : непосредственный // Технические науки: проблемы и перспективы : материалы II Междунар. науч. конф. (г. Санкт-Петербург, апрель 2014 г.). — Т. 0. — Санкт-Петербург : Заневская площадь, 2014. — С. 112-116. — URL: https://moluch.ru/conf/tech/archive/89/5465/ (дата обращения: 24.04.2024).
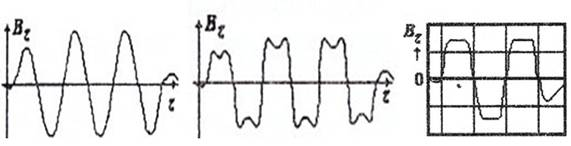
Известно, что для обеспечения фокусировки электронного потока в лампах бегущей волны (ЛБВ) применяются магнитные периодические фокусирующие системы (МПФС) различных видов [1]:
1) моногармонические МПФС (рис. 1а);
2) полигармонические МПФС (рис. 1б);
3) реверсивные МРФС (рис. 1в).
а) б) в)
Рис. 1. Продольное распределение магнитного поля в магнитных периодических фокусирующих системах (МПФС)
Возможность применения вейвлет-функций как аппроксимирующих функций для моделирования продольного распределения магнитного поля различных видов магнитных периодических фокусирующих систем (МПФС) рассмотрены в [1–3] и базируется на их графическом сходстве.
Моделирование всех видов МПФС, в том числе и полигармонических МПФС, разделено два основных этапа (рис. 2) [3]:
- моделирование продольного распределения магнитного поля ячейки МПФС (отдельного магнита);
- моделирование продольного распределения магнитного поля МПФС, которое реализуется с использованием реального механизма формирования распределения [4].
Для моделирования продольного распределения магнитного поля ячейки (отдельного магнита) полигармонических МПФС предложен подход, основанный на суммировании однополярных вейвлет-функций Гаусса второго порядка [1].
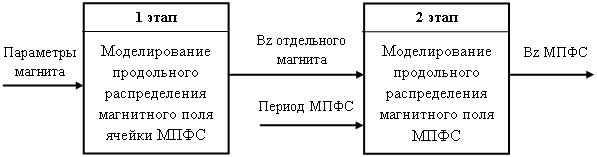
Рис. 2. Два этапа моделирования продольного распределения магнитного поля всех видов МПФС
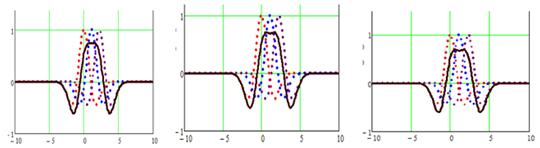
Рассмотрим формирование суммирующего распределения ячейки полигармонических МПФС, полученное суммированием двух (рис. 3а-в), трех (рис. 3г-е) и четырех (рис. 3ж-з) вейвлет-функций Гаусса второго порядка со сдвигом на величину S [1].

а) S=1.1 б) S=1.5 в) S=1.7
г) S=1.12 д) S=1.14 е) S=1.15
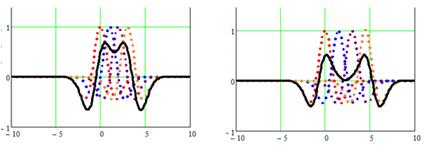
ж) S=1.01 з) S=1.5
Рис. 3. Суммирующее распределение ячейки (сплошная линия) из двух (а-в), трех (г-е) и четырех (ж-з) вейвлет-функций Гаусса второго порядка с различными значениями сдвига S
Из полученных суммирующих распределений ячеек (рис. 3) создаются распределение обратной полярности, чтобы образовать суммирующее распределение полигармонического МПФС. Для этого необходимо суммирующие распределения ячеек разной полярности сложить с учетом реального механизма формирования продольного распределения магнитного поля МПФС [5], сдвигая центры распределений ячеек на период МПФС [1]:
ТМПФС = S + 31/2 (1)
где S — сдвиг относительно центров двух соседних функций, 31/2 — абсцисса точки минимума функции.
Получим суммирующее распределение, по данной методике (рис. 4).
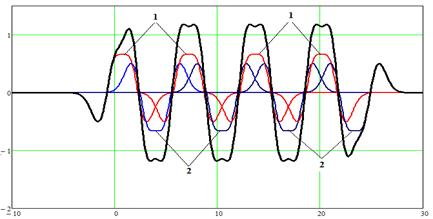
Рис. 4. Суммирующее распределение (сплошная линия) полигармонической МПФС из восьми суммирующих распределений: 1 — распределение (рис. 3а), 2 — обратное распределение
Составим алгоритм для моделирования продольного распределения магнитного поля полигармонической МПФС (рис. 5).
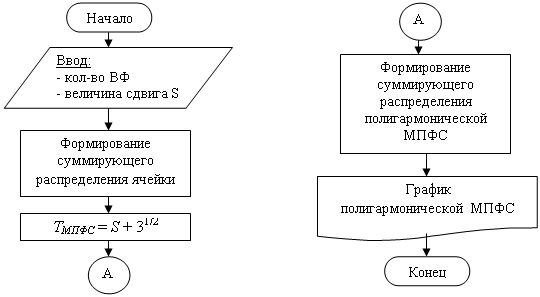 |
Рис. 5. Алгоритм моделирования продольного распределения магнитного поля полигармонической МПФС
На рис. 6 представлен листинг программы, позволяющий моделировать продольное распределение магнитного поля полигармонической МПФС в два этапа (см. рис. 2).
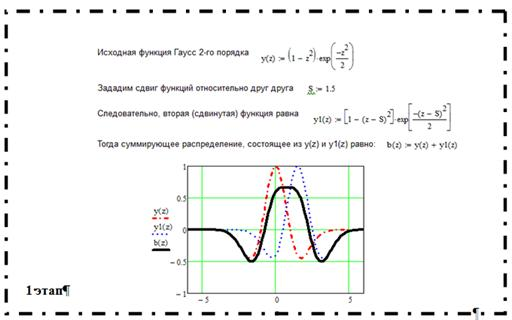
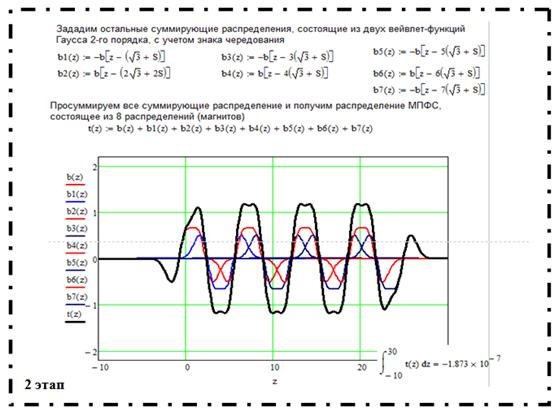
Рис. 6. Листинг программы моделирования продольного распределения магнитного поля полигармонической МПФС в среде MATHCAD
В дальнейшем планируется разработать пользовательское приложение, которое позволило бы моделировать продольное распределение магнитного поля различных видов МПФС с привязкой к параметрам магнитов, из которых состоит МПФС.
Литература:
1. Кожанова Е. Р., Захаров А. А., Ткаченко И. М. Применение вейвлет-функций Гаусса второго порядка для аппроксимации продольного распределения магнитного поля различных видов МПФС // Актуальные проблемы электронного приборостроения АПЭП — 2012: Материалы 10-й юбилейной международ. научно-технич. конференции (19–20 сентября 2012, Саратов). Саратов, 2010. С. 446–451.
2. Кожанова Е. Р., Захаров А. А. Применение модернизированной вейвлет-функции «Французская шляпа» для аппроксимации продольного распределения магнитного поля в магнитных реверсивных фокусирующих системах // Молодой ученый. 2012. № 9. С. 25–29.
3. Кожанова Е. Р., Захаров А. А., Ткаченко И. М. Возможность применение вейвлет-функции Гаусса первого порядка для моделирования магнитного поля реверсивных магнитных периодических систем // Молодой ученый. 2014. № 2. С. 149–152.
4. Кожанова Е. Р. Программа для моделирования продольного распределения магнитного поля магнитной реверсивной фокусирующей системы в среде MATHCAD // Новый университет. Серия: Технические науки. 2014. № 1. С.20–24.
5. Кожанова Е. Р., Захаров А. А. Формирование распределения суммирующих вейвлет-функций для моделирования продольного распределения магнитного поля магнитных периодических фокусирующих систем // Вестник Саратовского государственного технического университета. 2011. Т.4., № 1. С. 83–88.
Похожие статьи
Программное обеспечение для моделирования продольного...
магнитное поле, продольное распределение, вейвлет-функция Гаусса первого порядка, коэффициент сжатия, суммирующее распределение, модернизированная вейвлет-функция, различная полярность...
Возможность применение вейвлет-функции Гаусса первого...
Рис. 2. Суммирующее распределение (сплошная линия) из двух вейвлет-функций Гаусса второго порядка с различным значением смещения S [4]. - сложением двух функций: модернизированной вейвлет-функции «Французская шляпа» и двух...
Применение модернизированной вейвлет-функции «Французская...
По виду продольное распределение магнитного поля отдельного магнита, составляющего МРФС (рис. 3а), можно аппроксимировать знакопеременным распределением (пунктирная линия, рис. 3б), которое в свою очередь имеет схожесть с вейвлетом «Французская шляпа»...
Анализ структуры магнитного поля МПФС ЛБВ | Статья в журнале...
- моделирование продольного распределения магнитного поля ячейки МПФС (отдельного магнита). Применение модернизированной вейвлет-функции «Французская...» Магнитная реверсивная фокусирующая система (МРФС).
Использование программного продукта Elcut при решении задач...
продольное распределение, магнитное поле, программа расчета, отдельный магнит, математическая модель, магнитное поле ячейки, листинг программы расчета, графическая модель, вейвлет-функция Гаусса первого порядка...
Методы подавления счетного шума при решении задач физики...
Задача определения распределения электрического поля... Расчет проходили в несколько этапов: 1) Определение методом Гаусса -Зейделя значений функции в узлах области А и В.
Вычисление статистических показателей с использованием...
При проведении экспериментов или опытов получаются случайные величины, появление которых предсказать невозможно, и они чаще всего подчиняются нормальному закону распределения (закону Гаусса).
Похожие статьи
Программное обеспечение для моделирования продольного...
магнитное поле, продольное распределение, вейвлет-функция Гаусса первого порядка, коэффициент сжатия, суммирующее распределение, модернизированная вейвлет-функция, различная полярность...
Возможность применение вейвлет-функции Гаусса первого...
Рис. 2. Суммирующее распределение (сплошная линия) из двух вейвлет-функций Гаусса второго порядка с различным значением смещения S [4]. - сложением двух функций: модернизированной вейвлет-функции «Французская шляпа» и двух...
Применение модернизированной вейвлет-функции «Французская...
По виду продольное распределение магнитного поля отдельного магнита, составляющего МРФС (рис. 3а), можно аппроксимировать знакопеременным распределением (пунктирная линия, рис. 3б), которое в свою очередь имеет схожесть с вейвлетом «Французская шляпа»...
Анализ структуры магнитного поля МПФС ЛБВ | Статья в журнале...
- моделирование продольного распределения магнитного поля ячейки МПФС (отдельного магнита). Применение модернизированной вейвлет-функции «Французская...» Магнитная реверсивная фокусирующая система (МРФС).
Использование программного продукта Elcut при решении задач...
продольное распределение, магнитное поле, программа расчета, отдельный магнит, математическая модель, магнитное поле ячейки, листинг программы расчета, графическая модель, вейвлет-функция Гаусса первого порядка...
Методы подавления счетного шума при решении задач физики...
Задача определения распределения электрического поля... Расчет проходили в несколько этапов: 1) Определение методом Гаусса -Зейделя значений функции в узлах области А и В.
Вычисление статистических показателей с использованием...
При проведении экспериментов или опытов получаются случайные величины, появление которых предсказать невозможно, и они чаще всего подчиняются нормальному закону распределения (закону Гаусса).











