To the article touches upon some questions concerning the optimization process of driven rotation and drilling process with the criterion of minimum process costs. An analysis of reducing costs of drilling and boring processes is done, and the indexes influencing on basic price of cutting process are pointed out. The analysis of dependences of drilling speed is observed at different modes of cutting. The charts of dependences demonstrating a development of adaptive adjusting algorithm of drilling machines is performed.
Keywords:adaptive cutting; rotation, drilling and boring machine; rational modes; optimal modes of drilling.
В статье приведены некоторые вопросы оптимизации процесса вращательного бурения по критерию минимальной себестоимости процесса. Приведен анализ формирования стоимости процесса бурения, а также предложены показатели, влияющие на себестоимость процесса резания. Проведён анализ зависимостей скорости бурения при различных режимах резания. Построены графики зависимостей, которые наглядно показывающие необходимость разработки алгоритма адаптивного регулирования бурильных машин.
Ключевые слова: адаптивное резание; вращательное бурение; рациональные режимы; оптимальные режимы бурения.
An adaptive drive of boring installations or boring machines both have adaptive structures [1] and provide automatic maintenance of rational drilling modes. The concept «rational modes» includes various conditions of drilling and boring processes, for providing a maximum productivity of the process with minimum power consumption, and drilling costs. It is possible to say that the drilling modes can be sorted out in accordance with a certain target criteria. In a number of researches [2,3], the term «optimum modes of drilling» is widely used to describe a process reducing costs. Without any specification explaining the criterion «optimum», authors believe that it is an assumption mode where all drilling indicators of the process are supposed to be the best. However in different drilling modes we pay attention to this criterion which does not coincide with the meaning of the adjective the best [4]. Some leading experts in this field dealing with drilling machines [5], also point out that the main feature of drilling process is optimization so our research is an attempt to solve the problem of efficiency of the process [6]. We will compare two modes to be developed according to the actual data (see Fig. 1). Schedule 1 describes drilling modes with optimal data; schedule 2 describes drilling with overestimated results, in accordance to the present statement it is effective (we call this mode a power drilling).
For both modes, drilling cycle time is supposed to be tc and the depth of drilling for a cycle is Lc, is possible to see as:
tc = ∑ td + ∑ tr; Lc = ∑ Li,
where td is time of pure drilling, tr is time for a cutter replacement, Li is drilling depth of replacement of a cutter.
Then the speed of drilling or productivity of the process will have the following results:
Vd = Lc/tc = ∑ Li / ∑ td + ∑ tr;
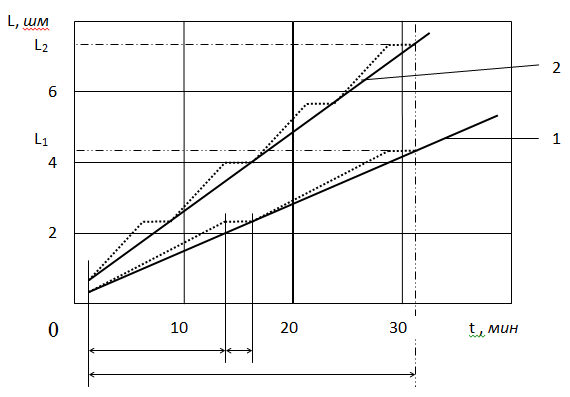
Fig. 1. The schedule of dependences of total depth is L for drilling time of t: where 1is for a relative mode to optimum, 2 for power drilling (Foc > Foc wholesale); the dotted line designating dependences of the actual drilling process
The actual speed of drilling, for the considered modes, is equal:
«Optimum» mode is: Vd = L1/tc
«Power drilling» is: Vd = L2/tc
The analysis of these dependences shows that at tc >> tr, the result of productivity will be increased in power drilling mode and it may be possible tz due to significant increase on cutter’s expenses and costs of drilling process. But sometimes a cutter is to be replaced, for example in drilling processes of strong breeds when td and tr are equal, the power mode increase can influence drilling productivity increase.
The power mode at tc >> tr is characterized by a bigger intensity of cutters when temperature of cutting edges is close to or equal to critical temperatures, thus the operating time of a cutter can be lowered twice (as it is provided on fig. 1) and even more times. Power drilling assumes the maximum specifications within strength restrictions and drive power restrictions.
When the «optimum» mode of drilling is picked out the cutters’ intensity should be much lower, then at drilling power in «non optimum» mode of drilling process. However power productivity of this mode is higher.
Designs of boring machines with the adaptive drive have to be based on drilling conditions with maximum speed operation, for example in extreme situations concerning people’s life or in other critical circumstances where everything depends on drilling velocity, so an «irrational» frequency of replacing cutting tools is required. Thus, it is necessary to provide reorganization of drilling algorithm in the power mode. It is obvious that development of managing system of a drilling process with temperature sensors at the cutting edge is highly actual for this mode of operation, so it is possible to perform drilling process in critical area and provide maximum velocity of drilling which will be more effective [7].
The cost of installing adaptive process of drilling machine in «optimum» mode and «power» mode is important for developing adaptive regulation algorithm and introducing additional correcting links to design adaptive boring machines.
The costs of stone drilling process Ccd can be set by the sum of two components with idle time costs Ci and expenses of drilling process Cpd: Ccd = Ci + Cpd.
Cutting process with an adaptive management influences only the second component of the process, but indirectly it is operating as a decrease of total expenses of drilling processes due to time decrease at prolonged and final operations and to decrease of cutting tool damages. We consider that mining material volume may be shown as drilling expenses with specific drilling costs Csd. This indicator can be demonstrated in the following way
Сsd =
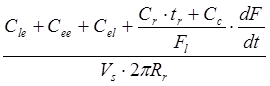(1)
Where: Cle are given labor expenses; Сee are given expenses on equipment; Cel are electric power costs; Cr is the cost of cutter’s replacement; Cc is cutter’s cost; Fl is a limit platform of a cutter; Vs is a giving speed; Rr is the radius of the drilled opening; dF/dt is the speed of degree changed sharpening process of a cutter.
For the majority of boring machines the control of drilling process is regulated by a given velocity and drill rotation velocity control. This adjusting can executed by the operator of the boring drilling and automatically. In practice of boring works, more often, frequency of rotation of boring barbell is not regulated, and the boring drilling is executed at permanent effort of serve. In situations, when the boring drilling is executed on a boundary path crosses breeds, for example, when the layers of soft breeds alternate and strong — this effort step can change operator, if this adjusting is envisaged in a boring machine. Analogical results are got and at the stand tests of adaptive boring machine [8].
Speed of degree influencing a cutter sharpening (dF/dt) depends on two regime parameters: a given speed of Vs and angular rotation speed of a drill of w (frequency of rotation of nr), thus it follows that the cost of drilling process depends only on these operated modes parameters. These variables are processing data and have to be varied in the course of drilling for ensuring minimizing costs. The last one represents the characteristic feature of process.
To determine dependence among the speed and meanings of variable cutting modes is a difficult task. we must pay attention to cutting tool if it is proportional to cutting time, i.e. intensity doesn't depend on the speed of cutting process/6/, so it is possible to get the following:
dF/dt = Сi ·
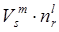, (2)
where: Ci is the coefficient characterizing cutting process and the characteristics of a destroyed material; m is an exponent of influence of a given velocity; l is an exponent of rotation frequency influencing a cutter; Vs is velocity.
At low rotation tool’s velocity it is possible to consider a vector of cutting speed as Vc is the geometric sum of velocity vectors of Vs and a linear speed of rotation- Vl = 2π Rr· nr, for a friction platform of cutting remote part with a rotation axis at the provided Rpr distance:
Vc =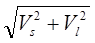 
= Vs·Vl ·
;
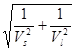Considering that Δ F is proportional to a way of friction of L during t for the quozy conditions we have:
dF/dt = Kc · Сi · Vs · nr (3)
where: Kc =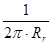
;
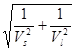For drilling mode with a certain range of considered variables it is possible to accept m and l as equal to unit, so we have:
dF/dt = Kf Vs· nr, (4)
where: Kf is a coefficient of strength and abrasive qualities of a destroyed material; Kr is a coefficient of a considered geometrical features of the tool and cutter’s material.
Expressions (1) and (4) applied for getting optimum conditions of adaptation taking into account a process of cutting part. It is possible to use a common equations (1) and (4), as a result we receive
Сsd =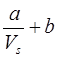 
· nr, (5)
where: a is the parameter characterizing the cost of an equipment and electric power; b is a parameter characterizing tool’s replacement process.
In Fig. 2 we have curves of a constant costs of the operating variables. These dependences can be received with the equation (5).
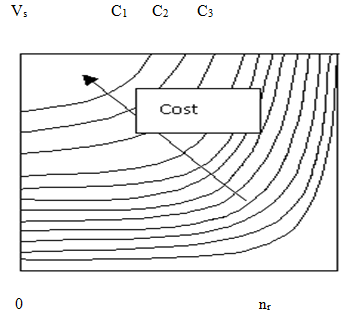
Fig. 2. Constant cost curve (indicators of drilling costs), C1 < C2 < C3
Apparently it is possible to reduce costs with the help of regulating drilling process, and increasing and reducing rotation velocities. We can substitute concrete conditions of drilling parameters and b, it is used to receive quantitative costs characteristics of drilling process.
It is necessary to emphasize that adaptive self-regulating process of a boring machine with the optimum mode using two different drives rovided by redistribution of rotation speed [9].
References:
1. Алимов О. А., Дворников Л. Г. Бурильные машины.–М.: Машиностроение, 1976. С. 295.
2. Волков Р. Ю. Исследование адаптивной бурильной машины с гидроприводом подачи вращения. //Альманах современной науки и образования. 2015. № 3 (93). С. 26–29.
3. Дровников А. Н. Анализ, синтез и разработка адаптивных механизмов: Автореф. дис… д-ра техн.наук // Казахский гос.ун-т, Алма-Ата: 1988.-32 с.
4. Дровников А. Н., Лемешко М. А. Структурная схема динамической модели «адаптивный буровой станок-забой».//Горный информационно-аналитический бюллетень (научно-технический журнал). 2003. № 8. С. 147–149.
5. Крапивин М. Г, Мамонтов В. Н., Ленченко В. В. Методы расчета режимов сверления крепких пород / Тр. НПИ. Т.244- Новочеркасск, 1972.С.49–54.
6. Лемешко М. А. Адаптивное управление процессом резания горных пород: монография // Лемешко М. А.; М-во образования и науки Российской Федерации, Гос. образовательное учреждение высш. проф. образования " Южно Российский гос. ун-т экономики и сервиса» (ГОУ ВПО «ЮРГУЭС»). Шахты, 2010, 67с.
7. Лемешко М. А. Стенд для исследования адаптивного процесса бурения с не сило-моментными обратными связями.// Горный информационно-аналитический бюллетень (научно-технический журнал). 2005. № 4. С. 314–315.
8. Лемешко М. А., Трифонов А. В. Исследование привода адаптивной машины «УБГ-1А». Горный информационно-аналитический бюллетень (научно-технический журнал). 2013. № 6. С. 202–207.
9. Лемешко М. А., Трифонов А. В. Математическая модель ограничений адаптивного управления машинами вращательного бурения. // Горный информационно-аналитический бюллетень (научно-технический журнал). 2012. № 2. С. 207–210.
