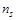Кластерная структура в дисперсно-наполненных композитах

В статье показано, что структура дисперсно-наполненных композитных материалов во многом зависит от качественного и количественного трансформирования кластеров в системе, и в частности от критического размера кластера.

Ключевые слова: композит, дисперсный наполнитель, кластер, структура, пороги протекания.

Новые композиционные материалы, появляющиеся вследствие стремления к совершенствованию уже существующих материалов и изделий, открывают широкие возможности для реализации перспективных конструктивных решений, технологических процессов, а также использования эффективных методов анализа, моделирования и прогнозирования.

От степени точности анализа и дальнейшего прогнозирования необходимых параметров композитных материалов, используемых в различных условиях эксплуатации, зависят надежность, долговечность и другие физико-технические свойства [1–3]. В этой связи, исследование физико-химических и эксплуатационных свойств композитных систем, и разработка моделей их прогнозирования, основанных на современных теориях кластерообразования, перколяции, бифуркации, структурно-фазовых переходов являются очень перспективными [4–6].

К подобным системам можно отнести моделирование и прогнозирование дисперсно-наполненных полимерных композитов. Например, с позиций кластерного анализа можно рассматривать упрочнение композитов дисперсными наполнителями [6–9], которое непосредственно связано с возникновением кластерных образований, представляющих собой в грубом приближении скопление частиц наполнителя, взаимодействующих между собой через пленочные прослойки матричной среды. Отдельные кластеры по существу являются центрами формирования новой кристаллоподобной структуры композита, обладающей повышенной упругостью и прочностью. В процессе роста кластера за счет присоединения к нему отдельных частиц происходит его качественное трансформирование в новую фазу с кристаллоподобными свойствами [10]. Причем такой переход осуществляется через неустойчивые состояния, связанные с частичным или полным распадом кластера. Поэтому в новую фазу переходят лишь те кластеры, размер которых превышает критическое значение. Впоследствии глобальное развитие кластерной структуры композита происходит в результате укрупнения закритических кластеров, за счет присоединения к ним неустойчивых кластеров и кластерных осколков.

Рис. 1. Элемент кластера в дисперсно-наполненном полимерном композите

Критический размер кластера определяется методом итерационно-экстраполяционного анализа данных, найденных для решеточных систем, и заключается в следующем. Устойчивость кластеров в немалой мере обусловлена дальнодействующим взаимодействием между составляющими его частицами, распространяющимся на дальние координационные группы. В таблице 1 приведены пороги протекания по узлам решеток, в которых связи между узлами (частицами) распространяются до третьей координационной группы. Известно, что произведение 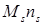 в пределе стремится к критическому числу 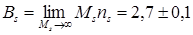, которое является универсальным и не зависит от типа решетки. Очевидно, что в случае реализации предельного значения  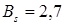под величиной  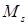подразумевается критическое число связанных узлов (частиц), которое в свою очередь определяет критический размер кластера. Для оценки критической величины  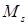проанализируем данные табл. 1.

В результате несложных вычислений определим среднеарифметические значения 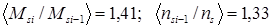, где 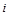 — номер решетки, указанный в табл.1. Пользуясь данными средних значений и величинам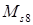и  и 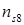 для последней из указанных в табл. 1 правильной решетки с плотнейшей упаковкой 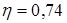, имеющей номер 8, найдем  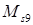и 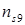 для решетки, связи между узлами которой распространяются до 4-й координационной группы 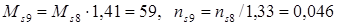. Умножение найденных чисел  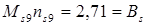дает весьма точное значение критического числа 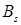, что подтверждает сделанный прогноз о структуре критического кластера.

Таблица 1

Пороги протекания по узлам с дальнодействующим взаимодействием

Следует отметить, что приведенная оценка размера критического кластера, включающего 59 узловых элементов, незначительно отличается от величины (55 узловых элементов), найденной Мюллером-Крумбхааром [4]. Связность между частицами в критическом кластере распространяется до 4-й координационной группы, а порог протекания по узлам при этом равен 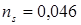. Условия критического кластера больше всего осуществимы в плотном клубковом кластере.

Поскольку взаимодействие центральной частицы клубкового кластера распространяется до 4-й координационной группы, можно сделать предположение, что в критическом кластере проявляется сильная дальнодействующая корреляция, приводящая к его силовой стабилизации под действием среднего поля. Такие кластеры обладают повышенной устойчивостью в условиях гидродинамических воздействий и вибраций. Кроме того, в процессе перемещения в объеме системы критические и закритические кластеры, подобно большим частицам, способны захватывать и присоединять к себе отдельные частицы и малые кластеры.

Таким образом, размер критического кластера имеет большое значение при оценке эффективности поверхностно-активных веществ (ПАВ). В этой связи свидетельством неэффективности ПАВ будет являться наблюдение в структуре композитов критических и закритических кластеров. Динамика развития, стабилизации, коалесценции критических кластеров позволяет более детально судить об усилении прочности, трещиностойкости, проницаемости, электропроводности и других свойств дисперсно-наполненных композитов.

Литература:

1.         Зубарев, П.А., Планирование оптимального соотношения компонентов в полиуретановой системе / П. А. Зубарев, В. О. Петренко, А. В. Лахно, Е. Г. Рылякин // Молодой ученый. 2014. — № 6 (65). — С. 164–166.

2.         Зубарев, П.А., Производственный процесс получения защитных полиуретановых покрытий / П. А. Зубарев, А. В. Лахно, Е. Г. Рылякин // Молодой ученый. 2014. — № 5 (64). — С. 57–59.

3.         Петренко, В. О. Моделирование оптимальной концентрации компонентов ремонтного клеевого состава / В. О. Петренко, А. В. Лахно, Е. В. Новиков Международный технико-экономический журнал. 2011. № 3. С. 110–112.

4.         Мюллер-Крумбхаар, Х. Моделирование малых систем / Х. Мюллер-Крумбхаар // Методы Монте-Карло в статистической физике. — М.: Мир, 1982. — С. 216–246.

5.         Бобрышев, А.Н. Анализ критического содержания наполнителя в композите с позиций теории перколяции / А. Н. Бобрышев, А. В. Лахно, П. В. Воронов, А. А. Бобрышев, Е. В. Новиков // Международный технико-экономический журнал. 2013. № 6. С. 93–98.

6.         Бобрышев, А. Н. Структура и свойства дисперсно-наполненных композитных материалов / А. Н. Бобрышев, А. В. Лахно, Р. В. Козомазов, А. А. Бобрышев. — Пенза: Изд-во ПГУАС, 2012. — 160 с.

7.         Лахно, А.В. Некоторые аспекты усиления полимерных композитов / А. В. Лахно, А. Н. Бобрышев, П. А. Зубарев, В. О. Петренко, Е. В. Новиков // Международный технико-экономический журнал. 2012. № 5. С. 100–105.

8.         Новиков, Е.В. Кластеро- и трещинообразование в композитах / Е. В. Новиков, А. В. Лахно, А. Н. Бобрышев, П. А. Зубарев // Международный технико-экономический журнал. 2012. № 5. С. 96–99.

9.         Бобрышев, А.Н., Анализ распределения наполнителя в структуре композитов // А. Н. Бобрышев, П. А. Зубарев, П. И. Кувшинов, А. В. Лахно // Интернет-Вестник ВолгГАСУ. 2012. № 1 (20). С. 28.

10.     Воронов, П.В. Оценка кинетики фазовых переходов в твердеющих гетерогенных материалах / П. В. Воронов, А. Н. Бобрышев, А. В. Лахно, П. И. Кувшинов, Н. Н. Туманова // Региональная архитектура и строительство. 2010. № 2. С. 58–66.