Embedding theorems of multi-weighted multi-parametric Sobolev spaces on domains with arbitrary shapes are obtained. Conditions on weight functions 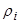
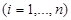 ,
, 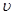 and at which the inequality of an investment is fair are received
and at which the inequality of an investment is fair are received 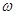
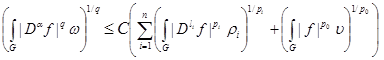 .
.
Examples with proofs are resulted.
Let 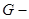 area in
area in 
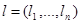 ,
, 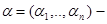 vectors with the whole coordinates
vectors with the whole coordinates 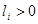 ,
, 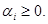
Below we will use designations: for
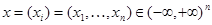 ,
, 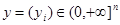 ,
, 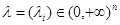 ,
, 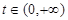
Let 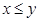 ,
, 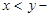 record of pokoordinatny comparison,
record of pokoordinatny comparison,
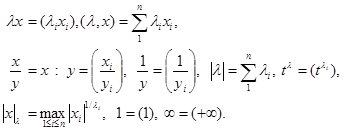
For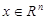 , sets
, sets 
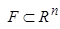 , and
, and 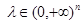 let
let
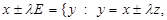
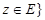 ,
, 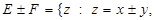
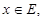
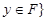 .
.
Let 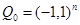 , area
, area 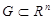 ,
,
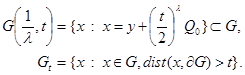
Let further 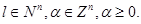
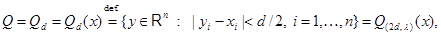
at 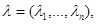
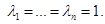 We will put
We will put
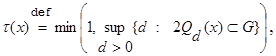
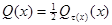 ,
,
and let
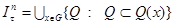 .
.
Through 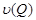 ,
, 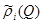 ,
, 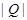 will be designated, respectively
will be designated, respectively 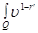 ,
, 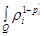 ,
, 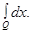 For a multiindex
For a multiindex 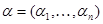
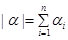 , for
, for 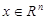
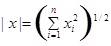 ;
;
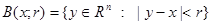 .
.
Through 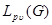 , the weight Lebesgue space with norm will be designated
, the weight Lebesgue space with norm will be designated
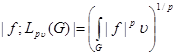 .
.
Below record 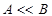 will mean that
will mean that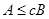 .
.
Definition 1 ([1]). Domain 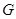 we will call if
we will call if 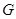 area with a condition of a flexible
area with a condition of a flexible 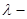 horn (a flexible cone at
horn (a flexible cone at 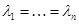 ) if at some
) if at some 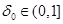 ,
, 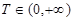 for
for 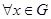 there is a curve
there is a curve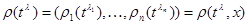
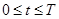 , with the following properties:
, with the following properties:
(a) for all 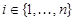
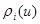 it is absolutely continuous on
it is absolutely continuous on 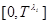 ;
; 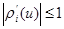 for the item of century.
for the item of century. 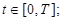
(b)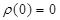
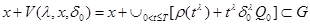 .
.
Let's put thus
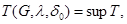
where the top edge takes on all 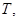 for which takes place the listed properties.
for which takes place the listed properties.
Lemma 1([2]). Let 
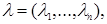
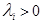 . Then from family of parallelepipeds
. Then from family of parallelepipeds 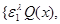
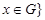 it is possible to take
it is possible to take 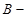 a covering
a covering 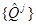 a set
a set 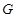 parallelepipeds
parallelepipeds 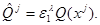 Thus family
Thus family 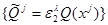 also forms
also forms 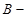
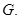 The Frequency rate covering
The Frequency rate covering 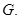 a covering
a covering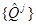 ,
, 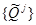 depend only from
depend only from 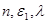 respectively
respectively 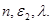
Lemma 2 ([2]). Let 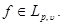 Then takes assessment place
Then takes assessment place
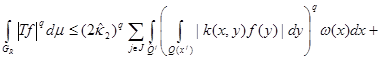
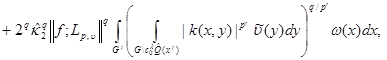
where 
Theorem. Let 
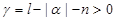 , and let weight
, and let weight 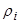
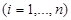 ,
, 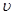 and
and 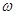 on
on 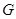 meet conditions: there is a regular function
meet conditions: there is a regular function 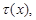 that
that
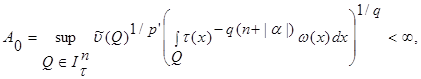
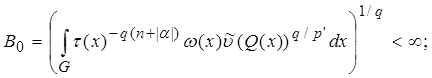
and
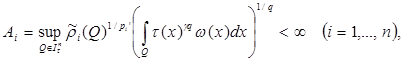
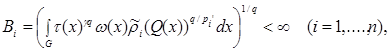
where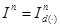 . Then the investment takes place
. Then the investment takes place
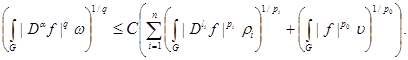 (1)
(1)
from an exact constant
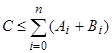 .
.
Proof. In these work [1, page 17] for functions 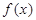 on area
on area 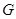 with a condition of a flexible
with a condition of a flexible 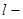 horn was received in particular, the following integrated representation:
horn was received in particular, the following integrated representation:
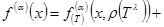
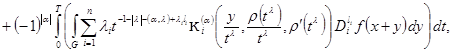 (2)
(2)
where
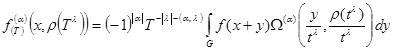 . (3)
. (3)
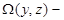 definite care,
definite care, 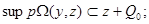
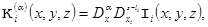
and 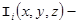 functions, satisfying the following conditions:
functions, satisfying the following conditions:
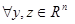 function (4)
function (4)
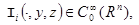
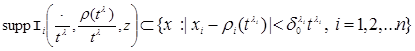 (5)
(5)
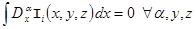 (6)
(6)
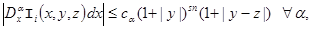 (7)
(7)
where 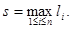
Let's copy representation (2) for 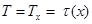 and considering conditions
and considering conditions 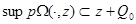 and (5):
and (5):
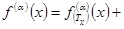
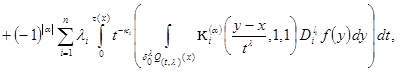 (8)
(8)
where 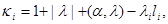 and
and
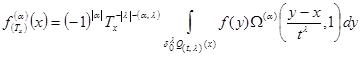 (9)
(9)
using integrated representation (8), (9), for a case 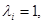
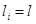
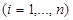 we write out
we write out
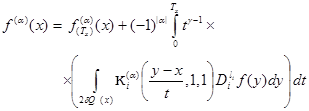 (10)
(10)
where 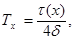
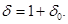 B (10) in conditions force (3), (7)
B (10) in conditions force (3), (7) 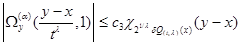 , we will receive
, we will receive
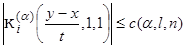 . (11)
. (11)
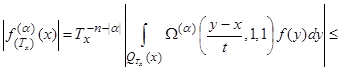
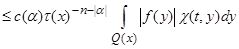 , (12)
, (12)
where 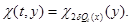
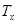 follows From a choice
follows From a choice 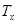 that
that 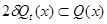 for all
for all 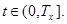 From (11) and conditions (4), (5) follows that
From (11) and conditions (4), (5) follows that
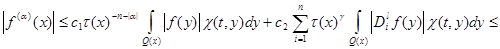
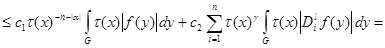 (13)
(13)
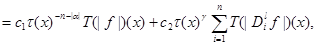
where 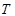 – the integrated operation with a care
– the integrated operation with a care
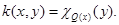
From (13) follows that
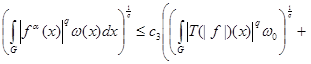
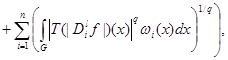 (14)
(14)
where
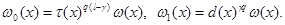
Let 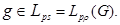 Owing to a lemma 2 for any
Owing to a lemma 2 for any 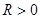 on
on
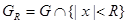
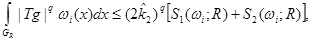 (15)
(15)
where
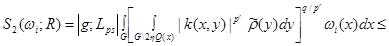
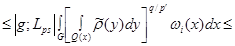 (16)
(16)
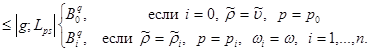
First composed in (15)
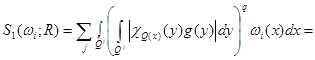
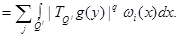 (17)
(17)
In (17) we will apply a lemma 1 in which for a kernel 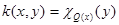 the following estimates are fair to an assessment of each integral
the following estimates are fair to an assessment of each integral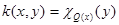 :
:
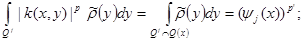
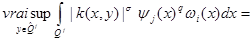
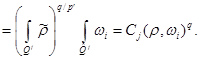
Owing to a lemma 1
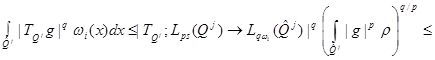
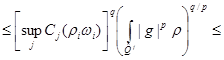 (18)
(18)
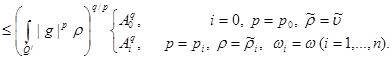
(17), (18) follows from estimates that
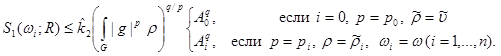
Having taken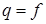 , at
, at 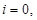
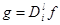 for
for 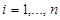 from
from 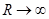 we remove that
we remove that
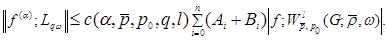
Example 1. Let's consider theorem conditions for permission of a question about existence of an inclusion
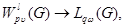
where 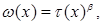
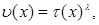
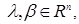
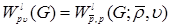
at
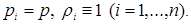
In this case for any cube 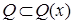
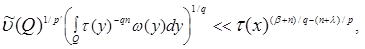
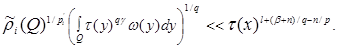
Therefore in order that
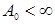 and
and 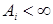
it is enough to demand that the following conditions were satisfied:
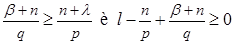 (19)
(19)
Further we have
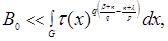
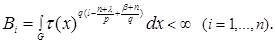
As well as
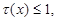 that
that 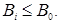
Let's say as 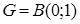 let
let 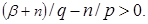 Then owing to (19)
Then owing to (19)
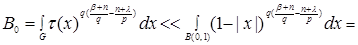
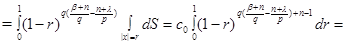
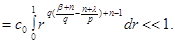
Let's consider more general case now, namely, let 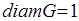 and for any
and for any 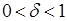 the surface
the surface 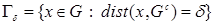 has the area
has the area 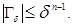 Then
Then
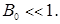
So, in these conditions on 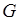 , the inclusion takes place
, the inclusion takes place
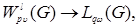
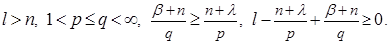
References:
1. O. V. Besov. Integrated representations of functions and the theorem of an inclusion for area with a condition flexible roga.//Works of Mathematical institute of Academy of Sciences of the USSR, 1984. T.170. Page 12–29.
2. Kusainova L. K. About limitation of one class of operators in weighted spaces of Lebega.//Works of inter@ konf. Semipalatinsk. 2003. Page 94–95.

