Работа посвящена разработке методики моделирования процесса взрывчатого разложения энергетических материалов с использованием метода конечных разностей с переменным шагом по координате.
Ключевые слова: математическое моделирование, разностная схема, переменный шаг по координате, цепная модель реакции, взрывное разложение, энергетические материалы, азид серебра.
The aim of this article is to simulate the explosion decomposition process of the energetic materials. The method of simulation based on the difference scheme with the variable spatial coordinate interval.
Keywords: simulation, difference scheme, variable spatial coordinate interval, chain reaction, explosive decomposition, energetic materials, silver azide.
Экспериментальное исследование кинетических закономерностей быстропротекающих процессов является трудоемкой и дорогостоящей задачей [1, c. 39, 2, c. 212, 3, c. 99]. В связи с развитием вычислительной техники значительную часть подготовительной работы рационально провести методами математического моделирования [4, c. 12, 5, c. 106, 6, c. 70]. Для этого необходимо разработать или модернизировать методики, позволяющие моделировать актуальные физико-химических процессы. Для быстропротекающих процессов взрывчатого разложения энергетических материалов таковыми являются процессы распространения света в прозрачной среде, содержащей наночастицы металлов [7, c. 686, 8, c. 750, 9, c. 127], поглощение света наночастицей [10, c. 14, 11, c. 197, 12, c. 7, 13, c. 63], нагрева металлических включений в инертных средах [14, c. 55, 15, c. 376, 16, c. 69], тепло- массопереноса [17, c. 23, 18, c. 38, 19, c. 97], инициирования взрывного разложения энергетических материалов за счет нагрева сильнопоглощающих включений лазерным импульсным излучением [20, c. 100, 21, c. 95, 22, c. 804]. Использование современных методик математического моделирования позволяет получить значительно больше информации о закономерностях процесса, чем этого можно достичь в эксперименте [23, c. 43, 24, c. 130, 25, c. 45]. Прикладной аспект заключается в разработке теории оптических детонаторов с использованием в капсюлях инициирующих и вторичных взрывчатых веществ [26, c. 341, 27, c. 93]. Целью работы является разработка методики моделирования процесса взрывчатого разложения энергетических материалов с использованием метода конечных разностей с переменным шагом по координате.
Метод конечных разностей с переменным шагом по координате
Для моделирования кинетики твердофазной реакции в случае, когда значительная часть инициирующего излучения поглощается в приповерхностной области, может быть использована разностная схема с переменным шагом по пространственной координате. В области собственного поглощения происходит значительное ослабление энергии при прохождении тонкого слоя образца. В этой области необходимо использовать значительно меньший шаг сетки — dx — такой, чтобы учесть экспоненциальное уменьшение энергии излучения при прохождении единичного слоя, при этом шаг должен уменьшаться при приближении к поверхности образца и увеличиваться при продвижении вглубь. Это, с одной стороны, позволит обеспечить необходимую точность расчетов, с другой — постепенное увеличение шага позволит сократить время расчета и снизит требования, предъявляемые к вычислительной технике.
Методика расчета включает в себя следующие стадии [28, c. 53]:
1) кристалл разбивается на отдельные ячейки, для каждой ячейки записывается система дифференциальных уравнений (ДУ);
2) при расчетах в декартовой системе координат используется переменный шаг по координате (100 ячеек с увеличивающимся шагом, 100 — с постоянным);
3) при решении системы ДУ используются граничные условия 3 рода.
Для задания сетки (первые 100 ячеек) можно воспользоваться геометрической прогрессией (рис. 1):
xn=aQn-1, (1)
где a1 — размер первой ячейки, Q — знаменатель геометрической прогрессии.
Переменный шаг по координате необходимо использовать для моделирования процесса в слое толщиной апог-1 (показатель поглощения внешнего излучения), затем для простоты расчетов можно перейти к использованию постоянного и равного xn=aQk-1 шага по координате. Можно использовать общую формулу для вычисления потоков в (1÷k) ячейках. Частное уравнение потока возникает для ячейки k, поскольку она являет граничной для перехода от сетки с переменным шагом к сетке постоянным шагом. Для ячеек k+1, k+2 можно воспользоваться уравнениями потоков [29, c. 3].

Рис. 1. Одномерная сетка с переменным шагом xn=aQk-1
Рассмотрим диффузионные потоки между соседними ячейками [15, c. 380]. Для начала определим геометрические параметры, используемые для вычисления потоков:
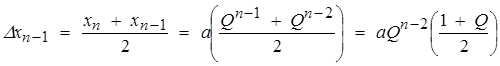 –
–
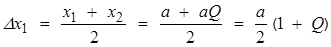 — расстояние между центрами ячеек c номерами n и n-1;
— расстояние между центрами ячеек c номерами n и n-1;
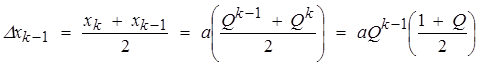 — расстояние между центрами ячеек k и (k-1), где k — индекс последнего члена геометрической прогрессии, для ячеек с номерами (k+1)÷kn размер ячеек постоянен;
— расстояние между центрами ячеек k и (k-1), где k — индекс последнего члена геометрической прогрессии, для ячеек с номерами (k+1)÷kn размер ячеек постоянен;
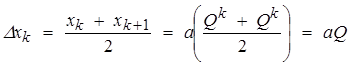 — расстояние между центрами ячеек c номерами k и (k+1), при постоянном шаге и одинаковом размере ячеек [10, c. 14].
— расстояние между центрами ячеек c номерами k и (k+1), при постоянном шаге и одинаковом размере ячеек [10, c. 14].
Площади сечения ячеек одинаковы (ΔSn=ΔS [5, c. 106]), поскольку рассматриваемые образцы в декартовой системе координат имеют постоянное поперечное сечение.
Уравнение для потока частиц в общем случае для n-ой ячейки, при изменении размеров ячеек [5, c. 106]:
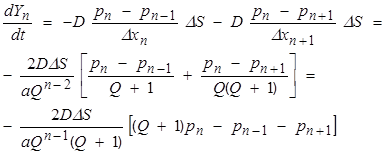 (2)
(2)
Разделив уравнение (2) на объем соответствующей ячейки получим уравнение, отражающее изменение концентрации [17, c. 23]:
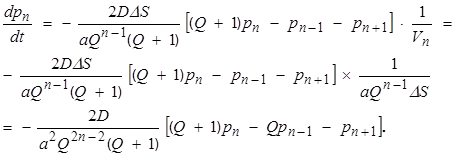 (3)
(3)
Для первой ячейки при расчете потока необходимо учесть рекомбинацию частиц на поверхности [19, c. 97] и обмен только с одной соседней ячейкой:
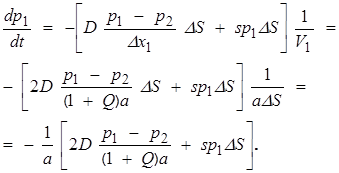 (4)
(4)
Для частиц в k-ой ячейке:
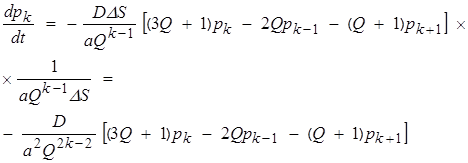 (5)
(5)
Уравнение для потока частиц в последней ячейке также будет иметь вид:
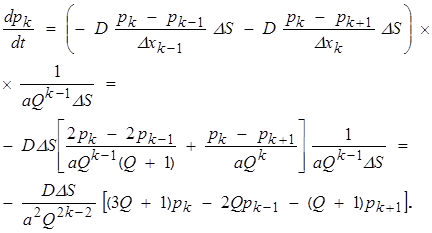 (6)
(6)
При моделировании кинетических закономерностей взрывчатого разложения энергетических материалов при различных показателях поглощения величины а и Q необходимо задавать таким образом, чтобы размер первой ячейки составлял не более 0.01/апог, первых 100 ячеек — 1/апог,, размер всего кристалла — не менее 0.1 см. Независимо от значения коэффициента поглощения ослабление интенсивности потока в первой ячейке происходит не более чем на 1 %.
Литература:
1. Адуев, Б. П. Взрывчатое разложение ТЭНа с нанодобавками алюминия при воздействии импульсного лазерного излучения различной длины волны / Б. П. Адуев, Д. Р. Нурмухаметов, Р. И. Фурега и др. // Химическая физика. — 2013. — Т. 32. — № 8. — С. 39–42.
2. Каленский, А. В. Взрывная чувствительность композитов тэн-алюминий к действию импульсного лазерного излучения / А. В. Каленский, И. Ю. Зыков, М. В. Ананьева и др. // Вестник КемГУ. — 2014. — № 3–3(59). — С. 211–216.
3. Каленский, А. В. Влияние длины волны лазерного излучения на критическую плотность энергии инициирования энергетических материалов / А. В. Каленский, А. А. Звеков, М. В. Ананьева и др. // Физика горения и взрыва. –2014. — Т. 50. — № 3. — С. 98–104.
4. Каленский, А. В. Коэффициент захвата электронных носителей заряда на экранированном отталкивающем центре/ А. В. Каленский, М. В. Ананьева, В. Г. Кригер, А. А. Звеков // Химическая физика. — 2014. — Т. 33. — № 4. — С. 11–16.
5. Кригер, В. Г. Взрывное разложение монокристаллов азида серебра при различных диаметрах зоны облучения / В. Г. Кригер, В. П. Ципилев, А. В. Каленский, А. А. Звеков// Физика горения и взрыва. — 2009. — Т. 45. — № 6. — С. 105–107.
6. Кригер, В. Г. Определение начала механического разрушения кристаллов азида серебра, инициированных лазерным импульсом / В. Г. Кригер, А. В. Каленский, А. А. Звеков // Физика горения и взрыва. — 2010. — Т. 46. — № 1. — С. 69 –72.
7. Zvekov, A. A. Regularities of light diffusion in the compo site material pentaery thriol tetranitrate — nickel / A. A. Zvekov, M. V. Ananyeva, A. V. Kalenskii and others // Наносистемы: физика, химия, математика. — 2014. — Т. 5. — № 5. — С. 685–691.
8. Звеков, А. А. Моделирование распределения интенсивности в прозрачной среде с Френелевскими границами, содержащей наночастицы алюминия / А. А. Звеков, А. В. Каленский, А. П. Никитин и др.// Компьютерная оптика. — 2014. — Т. 38. — № 4. — С. 749–756.
9. Адуев, Б. П. Исследование оптических свойств наночастиц алюминия в тетранитропентаэритрите с использованием фотометрического шара / Б. П. Адуев, Д. Р. Нурмухаметов, Г. М. Белокуров и др. // Журнал технической физики. 2014. Т. 84. № 9. С. 126–131.
10. Ananyeva, M. V. Comparative analysis of energetic materials explosion chain and thermal mechanisms / M. V. Ananyeva, V. G. Kriger, A. V. Kalensii and others // Известия высших учебных заведений. Физика. — 2012. — Т.55. — № 11–3. — С. 13–17.
11. Ананьева, М. В. Кинетические закономерности взрывного разложения ТЭНа, содержащего наноразмерные включения алюминия, кобальта и никеля / М. В. Ананьева, А. В. Каленский, Е. А. Гришаева и др. // Вестник КемГУ. — 2014. — № 1–1(57). — С. 194–200.
12. Ананьева, М. В. Перспективные составы для капсюля оптического детонатора / М. В. Ананьева, А. А. Звеков, И. Ю. Зыков и др. // Перспективные материалы. — 2014. — № 7. — С. 5–12.
13. Kalenskii, A. V. The Microcenter Heat Explosion Model Modernization / A. V. Kalenskii, V. G. Kriger, A. A. Zvekov and others // Известия ВУЗов. Физика. — 2012. — Т. 55. — № 11–3. — С. 62–66.
14. Кригер, В. Г. Влияние эффективности поглощения лазерного излучения на температуру разогрева включения в прозрачных средах / В. Г. Кригер, А. В. Каленский, А. А. Звеков и др.// Физика горения и взрыва. — 2012. — Т. 48. –№ 6. — С. 54–58.
15. Кригер, В. Г. Процессы теплопереноса при лазерном разогреве включений в инертной матрице / В. Г. Кригер, А. В. Каленский, А. А. Звеков и др. // Теплофизика и аэромеханика. — 2013. — Т. 20. — № 3. — С. 375–382.
16. Никитин, А. П. Расчет критических параметров инициирования теплового взрыва тэна с наночастицами меди на разных длинах волн / А. П. Никитин // Международное научное издание Современные фундаментальные и прикладные исследования.– 2013. — № 4(11).– С. 68–75.
17. Кригер, В. Г. Определение пространственных характеристик волны цепной реакции в азиде серебра / В. Г. Кригер, А. В. Каленский, А. А. Звеков и др. // Химическая физика. — 2014. — Т. 33. — № 8. — С. 22–29.
18. Боровикова, А. П. Пространственно-временные характеристики волны горения в азиде серебра / А. П. Боровикова, А. В. Каленский, И. Ю. Зыков // Аспирант. — 2014. — № 3. — С. 37–42.
19. Боровикова, А. П. Методика моделирования распространения взрывного разложения азида серебра / А. П. Боровикова, А. В. Каленский// Аспирант. — 2014. — № 4. — С. 96–100.
20. Зыков, И. Ю. Спектральная зависимость коэффициентов эффективности поглощения наночастиц серебра в прозрачной матрице / И. Ю. Зыков, О. В. Одинцова// Аспирант. — 2014. № 5. С. 99–102.
21. Газенаур, Н. В. Зависимость показателя поглощения меди от длины волны / Н. В. Газенаур, И. Ю. Зыков, А. В. Каленский // Аспирант. –2014. — № 5. — С. 94–98.
22. Kalenskii, A. V. Spectral regularities of the critical energy density of the pentaerythriol tetranitrate -aluminium nanosystems initiated by the laser pulse/ A. V. Kalenskii, M. V. Ananyeva // Наносистемы: физика, химия, математика. 2014. Т. 5. № 6. С. 803–810.
23. Боровикова, А. П. Природа стадии обрыва цепи разветвленных твердофазных цепных реакций / А. П. Боровикова, М. В. Ананьева, О. В. Одинцова// Молодой ученый. — 2014. — № 15(74). — С. 41–45.
24. Кригер, В. Г. Определение ширины фронта волны реакции взрывного разложения азида серебра / В. Г. Кригер, А. В. Каленский, А. А. Звеков и др. // Физика горения и взрыва. — 2012. — Т.48. — № 4. — С. 129–136.
25. Гришаева, Е. А. Неизотермическая модель разветвленной цепной реакции взрывного разложения энергетических материалов / Е. А. Гришаева, А. В. Каленский, М. В. Ананьева, А. А. Звеков// Фундаментальные проблемы современного материаловедения. — 2013. — Т. 10. — № 1. — С. 44–49.
26. Каленский, А. В. Спектральная зависимость критической плотности энергии инициирования композитов на основе пентаэритриттетранитрата с наночастицами никеля / А. В. Каленский, М. В. Ананьева, А. А. Звеков и др.// Фундаментальные проблемы современного материаловедения. — 2014. — Т. 11. — № 3. — С. 340–345.
27. Адуев, Б. П. Микроочаговая модель лазерного инициирования взрывного разложения энергетических материалов с учетом плавления / Б. П. Адуев, М. В. Ананьева, А. А. Звеков и др. // Физика горения и взрыва. 2014. Т. 50, № 6. С. 92–99.
28. Ананьева, М. В. Инициирование взрывного разложения микрокристаллов азида серебра / М. В. Ананьева, А. В. Каленский // Молодой ученый. — 2014. — № 19. — С. 52–55.
29. Ананьева, М. В. Математическое моделирование взрывного разложения энергетических материалов / М. В. Ананьева, А. В. Каленский // Молодой ученый. — 2014. — № 21. С. 1–6.
[1] Работа выполнена при финансовой поддержке РФФИ (грант № 14–03–00534 А) и Министерства образования и науки РФ (госзадание № 2014/64).

