В настоящее время заболевания сердечно-сосудистой системы являются наиболее распространенными в России. Многие из них [11] связаны с артериальным давлением (АД). АД — один из важнейших параметров, характеризующих работу кровеносной системы. Стойкое повышение АД выше 140/90 мм рт. ст. (артериальная гипертензия) или стойкое понижение АД ниже 90/50 мм рт. ст. (артериальная гипотензия) могут быть симптомами различных заболеваний (в простейшем случае гипертонии и гипотонии соответственно). К другим заболеваниям, связанным с АД, относятся ишемическая болезнь сердца, инфаркт миокарда, инсульт, сахарный диабет, аритмия.
Для наблюдения за этими болезнями и прогнозирования их развития важную роль играет математическое и имитационное моделирование. Его применение в биологии и медицине позволяет изучать процессы, о поведении которых нет полной экспериментальной информации. В большинстве работ математическое описание моделируемых систем осуществляется в терминах обыкновенных [6, 8] или стохастических [7, 9, 10] дифференциальных уравнений.
В настоящей работе построена математическая модель отклонения выше нормы систолического АД в моменты стрессовых ситуаций у человека, не больного гипертонией. Целью данной работы является компьютерная имитация результатов мониторирования верхнего давления у человека в возрасте 20—40 лет и построение оценки для ненаблюдаемой компоненты модели.
Экспериментальные данные были предоставлены ИМЭиФК УлГУ. Был проведен эксперимент, в котором у здорового человека измеряли систолическое АД в течение 24 часов. Всего было сделано 75 измерений, первые 39 измерений проводились с интервалом 15 минут, следующие 16 — с интервалом 30 минут. Для оставшихся 20 измерений длины интервалов чередовались.
АД человека значительно изменяется в течение дня в зависимости от его эмоционального и физического состояния. Часто повышенное АД вызвано различными стрессовыми ситуациями. Стресс — это общая реакция организма на воздействие (физическое или психологическое), нарушающее его гомеостаз (процесс саморегуляции), а также соответствующее состояние нервной системы организма (или организма в целом). Выделяют нервно-психический, тепловой или холодовый, световой, антропогенный и другие виды стресса [12]. Известно, что стресс ведет к синтезу в кровь большого количества стрессового гормона адреналина, под действием которого АД повышается. Чтобы нормализовать давление, в организме запускается процесс гомеостаза. В результате этого процесса уровень адреналина в крови понижается, что приводит к уменьшению уровня стресса и понижению АД.
Обозначим стохастический процесс содержания гормона адреналина в крови как 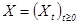 , время
, время 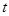 измеряется в часах. Количество адреналина, выбрасываемого в кровь в момент стрессовой ситуации, опишем процессом
измеряется в часах. Количество адреналина, выбрасываемого в кровь в момент стрессовой ситуации, опишем процессом 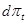 , где
, где 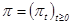 — стандартный пуассоновский процесс с интенсивностью
— стандартный пуассоновский процесс с интенсивностью 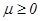 . Тогда процесс рассасывания адреналина в крови имеет вид
. Тогда процесс рассасывания адреналина в крови имеет вид 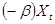 , где
, где 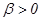 — пропорциональный коэффициент отрицательной обратной связи (коэффициент затухания).
— пропорциональный коэффициент отрицательной обратной связи (коэффициент затухания).
Обозначим стохастический процесс динамики систолического АД в мм рт. ст. как 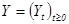 . Процесс увеличения АД под воздействием адреналина имеет вид
. Процесс увеличения АД под воздействием адреналина имеет вид 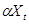 , где
, где 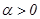 — пропорциональный коэффициент роста. Процесс гомеостаза обозначим как
— пропорциональный коэффициент роста. Процесс гомеостаза обозначим как 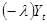 , где
, где 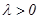 — пропорциональный коэффициент отрицательной обратной связи (коэффициент затухания). Процесс, включающий в себя остальные факторы, которые влияют на уровень АД (время года, температура воздуха, переедание, употребление кофе, медикаментов, вождение автомобиля и т. д.), обозначим как
— пропорциональный коэффициент отрицательной обратной связи (коэффициент затухания). Процесс, включающий в себя остальные факторы, которые влияют на уровень АД (время года, температура воздуха, переедание, употребление кофе, медикаментов, вождение автомобиля и т. д.), обозначим как 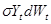 . Здесь
. Здесь 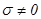 — пропорциональный коэффициент, а
— пропорциональный коэффициент, а 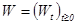 — стандартный винеровский процесс. Процессы
— стандартный винеровский процесс. Процессы 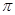 и
и 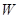 независимы.
независимы.
На основе математического описания медико-биологических процессов построим модель АД, заданную линейной системой стохастических дифференциальных уравнений
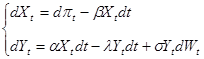 (1)
(1)
с начальными значениями 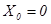 ,
, 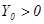 . Предполагается, что в системе (1) процесс
. Предполагается, что в системе (1) процесс 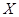 не наблюдаем, а наблюдать можно только процесс
не наблюдаем, а наблюдать можно только процесс 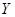 , который содержит неполную информацию о процессе
, который содержит неполную информацию о процессе 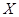 . Такая система называется частично-наблюдаемой.
. Такая система называется частично-наблюдаемой.
Процессы 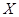 и
и 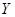 являются стационарными и эргодическими. Процесс
являются стационарными и эргодическими. Процесс 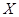 совершает скачки в моменты времени, совпадающие с моментами скачков пуассоновского процесса
совершает скачки в моменты времени, совпадающие с моментами скачков пуассоновского процесса 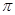 . Процесс
. Процесс 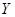 непрерывный, имеет множественные разладки. Моменты их возникновения также совпадают с моментами скачков процесса
непрерывный, имеет множественные разладки. Моменты их возникновения также совпадают с моментами скачков процесса 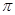 . Разладку можно интерпретировать как стрессовую ситуацию. Она компенсируется частично, роль компенсации играет процесс гомеостаза
. Разладку можно интерпретировать как стрессовую ситуацию. Она компенсируется частично, роль компенсации играет процесс гомеостаза 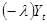 .
.
На основе модели (1) и выборки экспериментальных данных было проведено имитационное стохастическое моделирование, позволившее настроить параметры системы методом наименьших квадратов. Были получены следующие значения параметров:
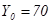 ,
, 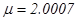 ,
, 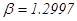 ,
, 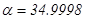 ,
, 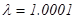 ,
, 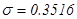 .
.
Поскольку в данной модели процесс 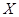 является ненаблюдаемым, ставится задача построения его оценки по наблюдениям за процессом
является ненаблюдаемым, ставится задача построения его оценки по наблюдениям за процессом 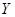 . Вид уравнений системы (1) похож на фильтр Калмана в общем случае, но применить к ним теорию оптимальной фильтрации мы не можем, так как обе компоненты фильтра Калмана должны быть непрерывными. В системе (1) процесс
. Вид уравнений системы (1) похож на фильтр Калмана в общем случае, но применить к ним теорию оптимальной фильтрации мы не можем, так как обе компоненты фильтра Калмана должны быть непрерывными. В системе (1) процесс 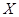 скачкообразный, поэтому сделаем замену, подставив вместо пуассоновского процесса
скачкообразный, поэтому сделаем замену, подставив вместо пуассоновского процесса 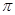 непрерывный процесс
непрерывный процесс 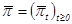 ,
, 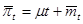 (2), где
(2), где 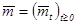 — непрерывный мартингал с
— непрерывный мартингал с 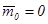 ,
, 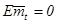 и
и 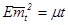 . Заметим, что формула (2) является непрерывным аналогом разложения Дуба — Мейера для пуассоновского процесса. Мы получили новую систему уравнений
. Заметим, что формула (2) является непрерывным аналогом разложения Дуба — Мейера для пуассоновского процесса. Мы получили новую систему уравнений
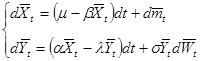 (3)
(3)
с начальными значениями 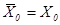 ,
, 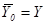 . Предполагается, что в системе (3) процесс
. Предполагается, что в системе (3) процесс 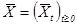 ненаблюдаемый, а процесс
ненаблюдаемый, а процесс 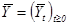 наблюдаемый. Очевидно, что оба процесса
наблюдаемый. Очевидно, что оба процесса 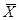 и
и 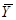 являются непрерывными.
являются непрерывными.
Система (3) представляет собой общий случай фильтра Калмана для двумерного частично-наблюдаемого процесса 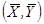 [2]. Выпишем для нее систему уравнений оптимальной фильтрации
[2]. Выпишем для нее систему уравнений оптимальной фильтрации
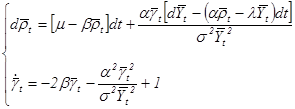 (4)
(4)
с начальными значениями 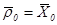 ,
, 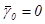 . Согласно теории,
. Согласно теории, 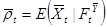 и
и 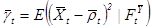 . Процесс
. Процесс 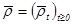 является оптимальной в среднеквадратическом смысле оценкой ненаблюдаемого процесса
является оптимальной в среднеквадратическом смысле оценкой ненаблюдаемого процесса 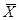 , а процесс
, а процесс 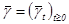 — оценкой отклонения
— оценкой отклонения 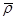 от
от 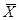 .
.
Для того чтобы оценить ненаблюдаемую компоненту 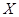 из системы (1), возьмем процесс
из системы (1), возьмем процесс 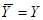 и подставим в (4). Получим систему уравнений
и подставим в (4). Получим систему уравнений
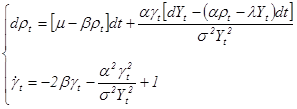 (5)
(5)
с начальными значениями 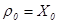 ,
, 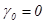 . В системе (5) процесс
. В системе (5) процесс 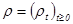 является теоретической оценкой процесса
является теоретической оценкой процесса 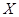 , а процесс
, а процесс 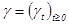 — теоретической оценкой отклонения
— теоретической оценкой отклонения 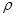 от
от 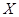 . Адекватность этих оценок была проверена с помощью стохастического имитационного моделирования. Полученные оценки
. Адекватность этих оценок была проверена с помощью стохастического имитационного моделирования. Полученные оценки 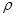 и
и 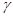 непрерывны.
непрерывны.
Заключение. В работе построена математическая имитационная модель динамики систолического АД, по которой можно пронаблюдать, как изменяется систолическое давление у здорового человека в моменты стрессовых ситуаций. Данная модель может быть усложнена в зависимости от конкретной решаемой задачи. Например, при добавлении в систему новых компонент, влияющих на АД, или функциональной зависимости параметров модели. Также была построена оценка для ненаблюдаемой компоненты системы с применением теории оптимальной фильтрации. Полученные в работе результаты применимы для решения широкого класса прикладных задач в различных областях современной биологии и медицины.
Автор выражает благодарность профессору Бутову А. А. за внимание к работе.
Литература
- Ширяев А. Н. Статистический последовательный анализ. — М.: Наука, 1976. — С. 251—259.
- Липцер Р. Ш., Ширяев А. Н. Статистика случайных процессов (нелинейная фильтрация и смежные вопросы). — М.: Наука, 1974. — С. 421—425.
- Бутов А. А. Элементы стохастического исчисления. Методическое пособие. — Ульяновск: УлГУ, 1996. — 24 с.
- Ширяев А. Н. Вероятность. — М.: Наука, 1989. — 640 с.
- Булинский А. В., Ширяев А. Н. Теория случайных процессов. — М.: ФИЗМАТЛИТ, 2005. — 408 с.
6. Марковский М. В., Ефимов А. В. Математическая модель динамики артериального давления // Научная сессия МИФИ-2000. Сборник научных трудов. — М., 2000. — Т. 2: Информатика и процессы управления. Информационные технологии. Сетевые технологии и параллельные вычисления. — С. 118—119. — Режим доступа: http://library.mephi.ru/data/scientific-sessions/2000/2/737.html, свободный.
7. Дюсупова А. К. Об одной модели регуляции артериального давления системой наиболее быстрых механизмов // ИВТ СО РАН: Тезисы докладов / «Конференция молодых учёных, посвящённая 10-летию ИВТ СО РАН», Новосибирск, Академгородок, 25—26 декабря 2000. — Новосибирск: 2000. — Режим доступа: http://www-sbras.nsc.ru/ws/show_abstract.dhtml?ru+9+1268, свободный.
8. Бияров Т. Н., Пыркова А. Ю. Импульсное управление динамическими системами на конечном отрезке времени. Математическая модель регуляции артериального давления при инсулинозависимом диабете // ИВТ СО РАН / «Конференция, посвященная 90-летию со дня рождения Алексея Андреевича Ляпунова», Новосибирск, Академгородок, 8—11 октября 2001. — Новосибирск: 2001. — Режим доступа: http://www.ict.nsc.ru/ws/Lyap2001/2265, свободный.
9. Чибисов С. М., Подладчикова Т. В., Рагульская М. В., Стрелков Д. Г. Оценка и прогноз результатов мониторирования среднего артериального давления у различных возрастных групп // Научные труды VIII Международного конгресса «Здоровье и образование в XXI веке. Концепции болезней цивилизации», 14—17 ноября 2007, РУДН. — М.: 2007. — С. 731—742. — Режим доступа: http://www.chronobiology.narod.ru/chibisovpodladchikova.html, свободный.
10. Подладчикова Т. В., Рагульская М. В., Чибисов С. М., Стрелков Д. Г. Долгосрочное мониторирование и математическое моделирование хронобиологических изменений среднего артериального давления у различных возрастных групп // Успехи современного естествознания. — М.: 2008. — № 2. — С. 14—20. — Режим доступа: http://www.rae.ru/use/pdf/2008/02/2008_02_02.pdf, свободный.
11. Заболевания, связанные с артериальным давлением // Электронное издание «Всё об артериальном давлении». — Режим доступа: http://www.120na80.ru/html/help.html, свободный.
12. Стрессы // Электронный словарь «Глоссарий.ru». — Режим доступа: http://www.glossary.ru/cgi-bin/gl_sch2.cgi?RRywlxx, свободный.







