Одним из способов получения качественных (отражающих закономерности протекания) характеристик компрессора является математическое описание процессов, происходящих в его элементах – решетках профилей, лопаточных венцах, рабочих колесах и направляющих аппаратах, в ступенях и в компрессоре в целом. Методам математического моделирования процессов в ГТД, в лопаточных машинах посвящено большое количество работ. Наиболее известными в этой области являются такие авторы, как Холщевников К.В., Емин О.Н., Федоров Р.М., Белоусов А.Н., Тунаков А.П. и др.
Однако в настоящее время еще не достаточно методик и обобщенных данных, которые бы уже на стадии проектирования нового компрессора позволили получать его характеристики, включая качественные и количественные данные по их протеканию. Для этого в работах [1] предлагается использовать обобщенные эмпирические зависимости. При этом, для того чтобы построить обобщенные характеристики ступени, т. е. зависимости 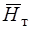 =f(
=f(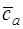 ) и
) и 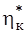 =f(
=f(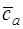 ), обычно предлагают выбрать и определить параметры ступени в расчетной точке (т. е. величины
), обычно предлагают выбрать и определить параметры ступени в расчетной точке (т. е. величины 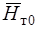 и
и 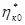 ). Считается, что рациональный выбор параметров ступеней компрессора на расчетном режиме поможет избежать проблемы попадания компрессора в область неустойчивых режимов из-за потери устойчивости первыми или последними ступенями. Однако не всегда параметры расчетного режима известны, часто на практике требуется определить влияние геометрии лопаток, решеток на характеристики ступени, каскада и МОК в целом. Кроме того, это полезно при обобщении характеристик компрессоров, ступеней, при планировании испытаний (в т.ч. определении границы помпажа) и при планировании численных 3D CAD/CAE- расчетов.
). Считается, что рациональный выбор параметров ступеней компрессора на расчетном режиме поможет избежать проблемы попадания компрессора в область неустойчивых режимов из-за потери устойчивости первыми или последними ступенями. Однако не всегда параметры расчетного режима известны, часто на практике требуется определить влияние геометрии лопаток, решеток на характеристики ступени, каскада и МОК в целом. Кроме того, это полезно при обобщении характеристик компрессоров, ступеней, при планировании испытаний (в т.ч. определении границы помпажа) и при планировании численных 3D CAD/CAE- расчетов.
В приведенных методиках приближенного расчета характеристик нерегулируемых осевых компрессоров [1,2] предлагается выбирать за «базовый» некоторый расчетный режим (в некоторых источниках предлагается использовать оптимальный режим, что неверно) и методика расчета сводится к тому, что сначала определяются параметры решетки компрессора на этом режиме и затем произведен расчет напорных ветвей, соответствующих этому режиму. При этом нет определенности, какой режим принимается за базовый – в одних источниках речь идет о «расчетном», в других о «номинальном», в третьих об оптимальном режимах. В то же время даются достаточно четкие определения номинального режима (где 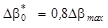 ), оптимального режима (где достигается максимум КПД - ступени или компрессора). Графики и приводимые эмпирические зависимости противоречат друг другу, в них много ошибок.
), оптимального режима (где достигается максимум КПД - ступени или компрессора). Графики и приводимые эмпирические зависимости противоречат друг другу, в них много ошибок.
Поэтому, в связи с разработкой в НИЛ САПР-Д УГАТУ систем имитационного моделирования компрессоров (СИМ KOMPR, STUPENY и т.д.), с участием авторов проведен анализ экспериментальных данных, различных эмпирических и теоретических зависимостей, выведен ряд собственных зависимостей и предложена следующая методика. В соответствии с ней предлагается брать за расчетный режим именно номинальный, который отличается от оптимального, т.е. расчетный режим отдельных ступеней смещен по отношению к режиму с максимальным КПД и находится в области с более низким КПД, но с более высоким запасом устойчивости.
Для расчета выведен ряд дополнительных формул и предложена комбинация использования зависимостей, обнаруженных Ольштейном Л.Е. и Хауэлом. Последняя дополнительно уточняется по зависимостям, приведенным Холщевниковым К.В. Для иллюстрации предложенной методики ниже приведен расчет характеристики первой ступени компрессора низкого давления (КНД) ГТП АЛ-31СТ.
Расчет упрощенной характеристики 1 ступени КНД АЛ-31СТ
В качестве исходных данных для данного расчета приняты следующие геометрические параметры 1ст. КНД АЛ-31СТ: 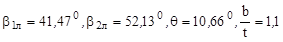 ,
, 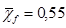 (сверхзвуковая решетка), угол выхода из ВНА
(сверхзвуковая решетка), угол выхода из ВНА 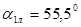 (рис. 1.)
(рис. 1.)
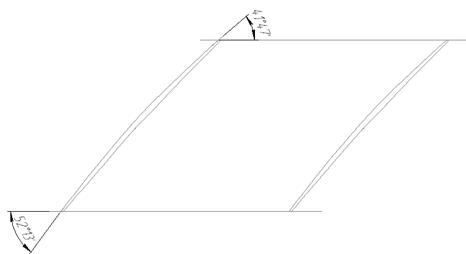
Рис. 1. Решетка профилей лопаток 1ст. КНД АЛ-31СТ
Последовательность определения 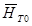 ,
, 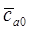 ,
, 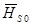 и
и 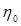 :
:
1. Для получения параметров, характеризующих номинальный режим
необходимо построить зависимость 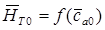 . Упрощенно это делается по формуле Хауэла
. Упрощенно это делается по формуле Хауэла 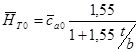 . Более точно это можно сделать по зависимостям, приведенным в [1], для этого для данной густоты построены зависимости
. Более точно это можно сделать по зависимостям, приведенным в [1], для этого для данной густоты построены зависимости 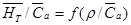 (1), после преобразований получаем искомую зависимость (рис.2)
(1), после преобразований получаем искомую зависимость (рис.2)
2. Учитывая, что с учетом закрутки за ВНА 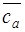 =
=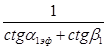 , строим линию идеального теоретического напора (при нулевом угле отставания на выходе из РК)
, строим линию идеального теоретического напора (при нулевом угле отставания на выходе из РК) 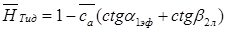 (в данном случае это луч, идущий из т.{1;0} в т. {0;0,6826} (рис. 2)
(в данном случае это луч, идущий из т.{1;0} в т. {0;0,6826} (рис. 2)
3. Определяем значения 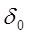 и
и 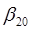 на номинальном режиме, где по определению
на номинальном режиме, где по определению 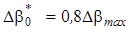 . В [2,3] предложена эмпирическая зависимость
. В [2,3] предложена эмпирическая зависимость 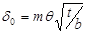 , (2), при этом в [1] эта же формула записана неверно (под корнем записана густота решетки). Сразу отметим, недостатком этой формулы является то, что она не годится для решеток из пластин, где
, (2), при этом в [1] эта же формула записана неверно (под корнем записана густота решетки). Сразу отметим, недостатком этой формулы является то, что она не годится для решеток из пластин, где 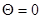 , для этого случая в предложенной методике используется специальное «ответвление». Пока рассматриваем вариант
, для этого случая в предложенной методике используется специальное «ответвление». Пока рассматриваем вариант 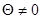 . В [3] приведена зависимость
. В [3] приведена зависимость 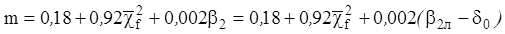 , (здесь авторами, после сравнения с аналогичной, но менее удобной зависимостью из [2], и сравнения с эмпирическими данными знак «-» сменен на «+» перед 0,002
, (здесь авторами, после сравнения с аналогичной, но менее удобной зависимостью из [2], и сравнения с эмпирическими данными знак «-» сменен на «+» перед 0,002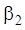 ). После преобразований получена зависимость для угла отставания на номинальном режиме:
). После преобразований получена зависимость для угла отставания на номинальном режиме:
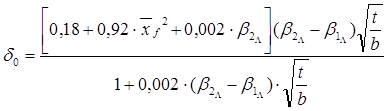 (2)
(2)
Для рассматриваемого примера:
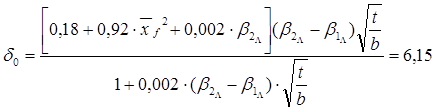
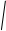
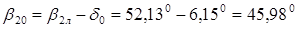
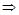
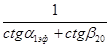 =0,605
=0,605
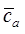
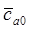
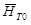
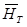
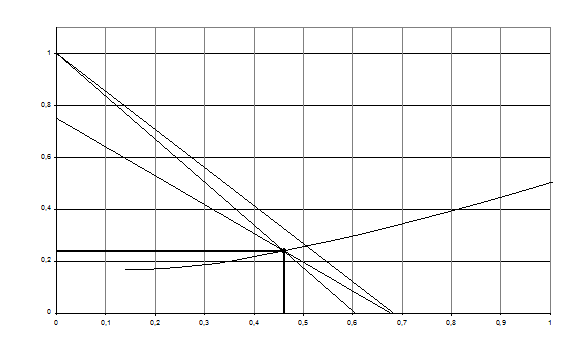
Рис.2. Один из этапов построения упрощенной характеристики 1 ст. КНД АЛ-31СТ 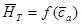 по геометрии решеток, на основе предложенного авторами метода использования эмпирических (обобщенных) зависимостей Ольштейна Л.Е. и Хауэлла.
по геометрии решеток, на основе предложенного авторами метода использования эмпирических (обобщенных) зависимостей Ольштейна Л.Е. и Хауэлла.
4. Проводим луч из т.{1;0} с учетом угла отставания на номинальном режиме – в точку на оси абсцисс 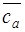 =
=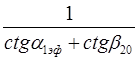 . Авторами показано, что именно этот луч характеризует номинальный режим на кривой
. Авторами показано, что именно этот луч характеризует номинальный режим на кривой 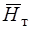 =f(
=f(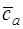 ). В рассматриваемом примере луч проходит на оси абсцисс через точку {0;0,605} и определяется на пересечении с лучом Хауэлла номинальный режим, где значения
). В рассматриваемом примере луч проходит на оси абсцисс через точку {0;0,605} и определяется на пересечении с лучом Хауэлла номинальный режим, где значения 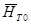 = 0,24 и
= 0,24 и 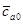 =0,46.
=0,46.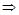
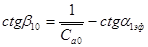 = 1.4866
= 1.4866 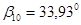
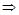
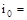 7,540.Через эту точку в рассматриваемом примере будет проходить график теоретического напора
7,540.Через эту точку в рассматриваемом примере будет проходить график теоретического напора 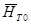 . Более точное аналитическое определение номинального режима:
. Более точное аналитическое определение номинального режима:
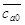 =
=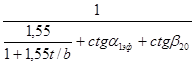 =0,46,
=0,46,
что подтверждает графоаналитический расчет.
Располагая графиками эмпирических зависимостей из [1] изменения коэффициентов 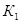 и
и 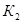 , полученными значениями
, полученными значениями 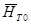 = 0,24 и
= 0,24 и 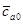 =0,46. можно по выражению
=0,46. можно по выражению 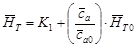 (3) построить требуемую кривую
(3) построить требуемую кривую 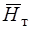 =f(
=f(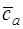 ). Авторами показано, что аппроксимация эмпирической зависимости для
). Авторами показано, что аппроксимация эмпирической зависимости для 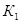 в зоне
в зоне 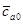 <1 сводится к лучу, идущему из точки на оси ординат
<1 сводится к лучу, идущему из точки на оси ординат 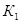 =0,75. Это позволяет легко построить
=0,75. Это позволяет легко построить 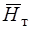 =f(
=f(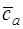 ), как это показано на рис.2 для М<=0,4.
), как это показано на рис.2 для М<=0,4.
5. Далее необходимо определить коэффициент изоэнтропического напора и КПД ступени на расчетном (номинальном) режиме. Для этого воспользуемся зависимостями
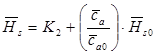 (4)
(4)
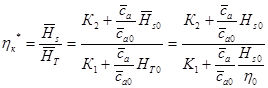 (5)
(5)
Аппроксимируя графики 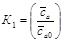 и
и 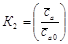 [1,2], получаем:
[1,2], получаем: 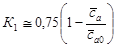 - луч
- луч и касательная в точке
и касательная в точке 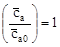 к графику нелинейной зависимости
к графику нелинейной зависимости 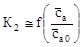 - луч
- луч 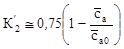 . Из этого следует, что при
. Из этого следует, что при 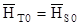 и
и 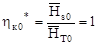 , максимум кривой
, максимум кривой 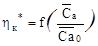 находится на вертикали
находится на вертикали 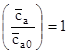 . При
. При 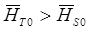
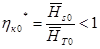 и максимум кривой
и максимум кривой 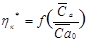 смещается влево
смещается влево 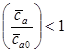 . Величина этого смещения и значения
. Величина этого смещения и значения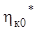 и
и 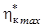 взаимно обусловлены (чем ближе
взаимно обусловлены (чем ближе 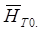 к
к 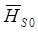 , т. е. чем ближе
, т. е. чем ближе 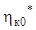 к 1, тем правее точка максимума КПД, тем ближе и сам оптимальный режим к номинальному режиму и наоборот).
к 1, тем правее точка максимума КПД, тем ближе и сам оптимальный режим к номинальному режиму и наоборот).
Анализ графиков [1] показывает, что максимум КПД ступени 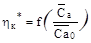 находится вблизи точки
находится вблизи точки 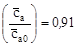 . Это позволяет подобрать значение
. Это позволяет подобрать значение 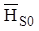 , проводя в первом приближении касательную к кривой
, проводя в первом приближении касательную к кривой 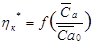 как луч из т. {0,75;0} в точку {0;0,605}- в ту же точку на оси абсцисс
как луч из т. {0,75;0} в точку {0;0,605}- в ту же точку на оси абсцисс 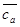 =
=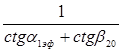 , куда приходит построенный на первом этапе луч из т. {1;0} (рис. 3).
, куда приходит построенный на первом этапе луч из т. {1;0} (рис. 3).
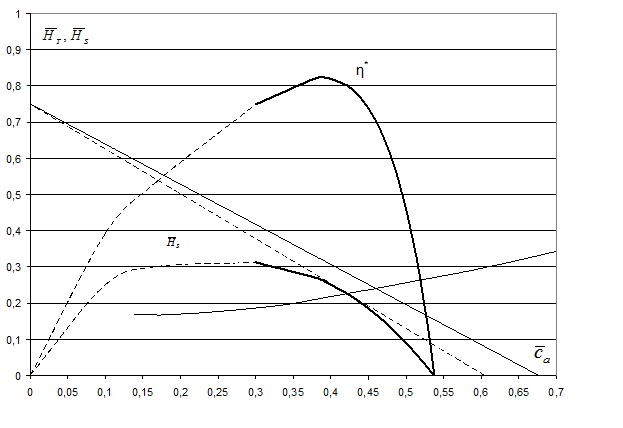
Рис.3. Построение характеристики 1 ступени КНД АЛ-31СТ 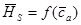 и
и 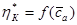 на основе геометрии решеток, с предложенным авторами методом использования эмпирических (обобщенных) зависимостей Ольштейна Л.Е. и Хауэлла.
на основе геометрии решеток, с предложенным авторами методом использования эмпирических (обобщенных) зависимостей Ольштейна Л.Е. и Хауэлла.
Это позволяет уже на первом этапе почти точно определить КПД на номинальном режиме, в данном случае 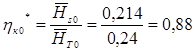 . Далее, поворотом луча, касательного к кривой К2 и самой кривой
. Далее, поворотом луча, касательного к кривой К2 и самой кривой 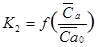 по простому алгоритму строится кривая
по простому алгоритму строится кривая 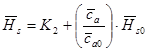 , затем строится кривая
, затем строится кривая 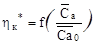 по результатам расчета
по результатам расчета 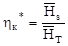 и проверяется, где находится максимум КПД. При необходимости, уточняя значение
и проверяется, где находится максимум КПД. При необходимости, уточняя значение 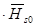 , добиваемся требуемого положения кривой
, добиваемся требуемого положения кривой 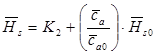 , при котором положение максимума кривой
, при котором положение максимума кривой 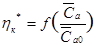 окажется на вертикали
окажется на вертикали 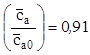 . В данном случае это
. В данном случае это 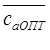 =0,395.
=0,395.
Далее задаемся диапазоном изменения 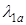 [0;1]. Записывая изоэнтропическую работу, как
[0;1]. Записывая изоэнтропическую работу, как 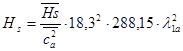 , строим график
, строим график 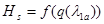 с изолиниями
с изолиниями 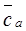 = const (рис 4). При этом самая верхняя изолиния
= const (рис 4). При этом самая верхняя изолиния 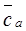 = const характеризует границу помпажа. Сами изолинии
= const характеризует границу помпажа. Сами изолинии 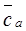 = const в координатах
= const в координатах 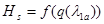 описываются зависимостью
описываются зависимостью 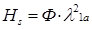 .
.
Для этого предварительно по ранее полученной кривой 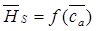 находим
находим 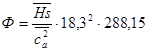 и строим график
и строим график 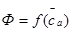 (рис. 5). Находим изоэнтропическую работу
(рис. 5). Находим изоэнтропическую работу 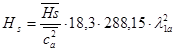 и строим график
и строим график 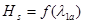 (рис. 4).
(рис. 4).
Опыт показал, что результаты построения кривой 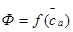 требуют проверки. Дело в том, что сама используемая кривая
требуют проверки. Дело в том, что сама используемая кривая 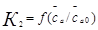 нами существенно экстраполирована к началу координат. В то же время известно, что она ведет себя по-разному в зависимости от относительного удлинения лопатки. В данном случае лопатка короткая и должна быть характерная «ступенька» вблизи области срыва на кривой
нами существенно экстраполирована к началу координат. В то же время известно, что она ведет себя по-разному в зависимости от относительного удлинения лопатки. В данном случае лопатка короткая и должна быть характерная «ступенька» вблизи области срыва на кривой 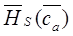 . Проверка состоит в нанесении на изолинии
. Проверка состоит в нанесении на изолинии 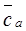 = const в координатах
= const в координатах 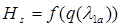 дополнительно напорных веток
дополнительно напорных веток 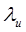 = const, что легко сделать по формуле
= const, что легко сделать по формуле 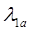 =
=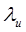 ×
×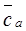 .
.
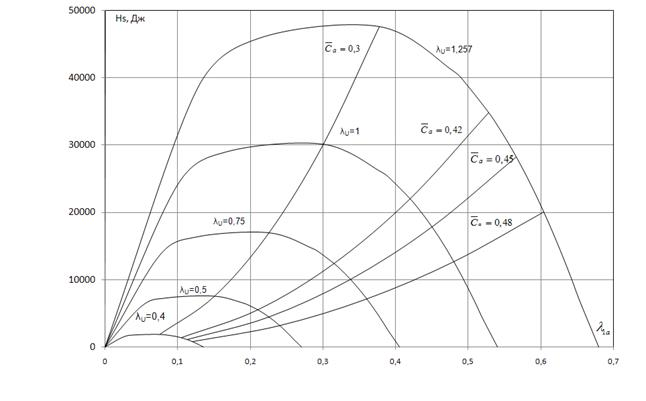
Рис. 4 Характеристика первой ступени КНД АЛ31-СТ 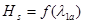
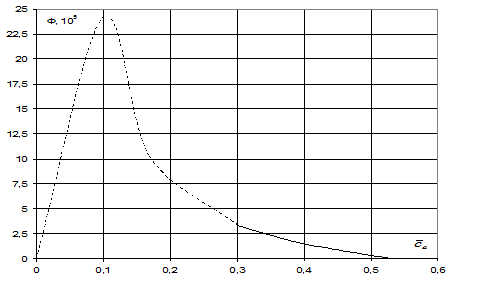
Рис. 5 Характеристика первой ступени КНД АЛ31-СТ 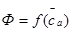
Линия 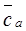 = const выявляется по признаку – на ней напорные ветки
= const выявляется по признаку – на ней напорные ветки 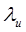 = const достигают максимума и касательная к ним горизонтальна:
= const достигают максимума и касательная к ним горизонтальна: 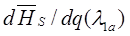 =0. Все изолинии
=0. Все изолинии 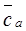 = const, проходящие выше и левее, для которых у напорных веток
= const, проходящие выше и левее, для которых у напорных веток 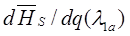 <0, считаются нереальными и отбрасываются. Это, в свою очередь, позволяет поправить экстраполяцию кривой
<0, считаются нереальными и отбрасываются. Это, в свою очередь, позволяет поправить экстраполяцию кривой 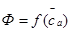 и кривой
и кривой 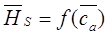 . В данном случае выявлено, что максимум кривой
. В данном случае выявлено, что максимум кривой 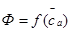 должен находиться в точке
должен находиться в точке 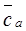 =0,3 при этом, этой изолинии соответствует граница помпажа, где
=0,3 при этом, этой изолинии соответствует граница помпажа, где 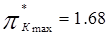 Полученный результат нетрудно представить в традиционных координатах
Полученный результат нетрудно представить в традиционных координатах 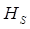 =
=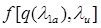 (рис. 6) и
(рис. 6) и 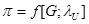 (рис. 7). На приведенных графиках не показаны режимы запирания, возникающие в «горле» РК или НА. Как известно, после достижения этих режимов, напорные ветви становятся вертикальными. Для построения линии запирания, зоны «сгущения», в т.ч. предельной точки, где «горло» решетки РК 1 ступени запирается и в относительном, и в абсолютном движении, авторами предложена отдельная методика, которая будет рассмотрена в следующей статье.
(рис. 7). На приведенных графиках не показаны режимы запирания, возникающие в «горле» РК или НА. Как известно, после достижения этих режимов, напорные ветви становятся вертикальными. Для построения линии запирания, зоны «сгущения», в т.ч. предельной точки, где «горло» решетки РК 1 ступени запирается и в относительном, и в абсолютном движении, авторами предложена отдельная методика, которая будет рассмотрена в следующей статье.
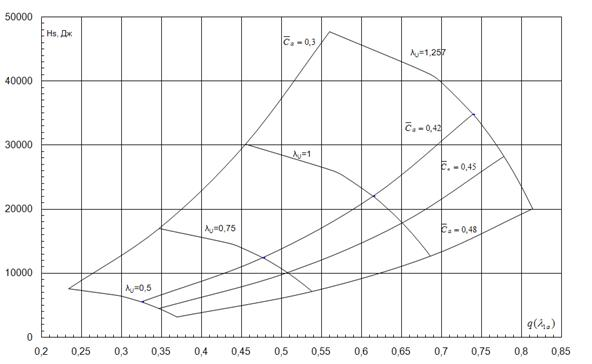
Рис. 6 Характеристика первой ступени компрессора АЛ31-СТ 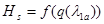
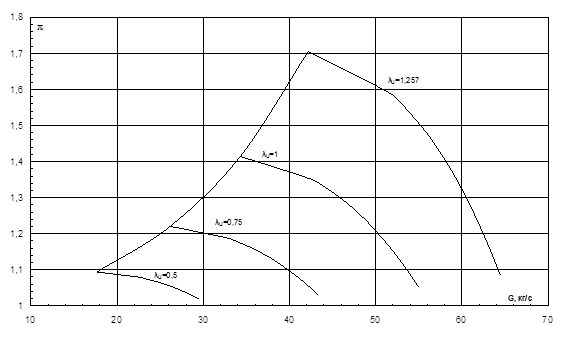
Рис. 7 Характеристика первой ступени компрессора АЛ31-СТ 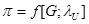
Заключение
Выполненные расчеты характеристик (с использованием обобщенных экспериментальных данных), показывают, что, на основе геометрии решеток можно с определенной точностью получить характеристики ступени и компрессора в целом без экспериментальных исследований по продувке решеток или испытаний компрессора, либо спланировать такой физический или численный эксперимент. Характеристика всего компрессора может быть получена путем сложения характеристик его ступеней – по предложенному алгоритму или с использованием СИМ (системы имитационного моделирования) компрессора с разбиением на ступени.
Список литературы
1. Холщевников К.В. Теория и расчет авиационных лопаточных машин : Учеб. для авиац.вузов и фак. — М. : Машиностроение, 1970 .— 610с.
2. Холщевников, К. В. Теория и расчет авиационных лопаточных машин: [учебник для студентов вузов, обучающихся по специальности "Авиационные двигатели ""] / К. В. Холщевников, О. Н. Емин, В.Т. Митрохин .— 2-е изд., перераб. и доп. — М.: Машиностроение, 1986
3. Белоусов А. Н. Теория и расчет авиационных лопаточных машин: / А. Н. Белоусов,
Н. Ф. Мусаткин, В. М. Радько.— Самара: Сам. Дом Печати, 2003 .— 344 с.

