Известно [1..3], управляющие воздействия оператора в эргатической системе в большинстве случаев определяются собственными частота и коэффициентами демпфирования затухающих колебаний. По оценке операторов наиболее комфортным считается управление объектом, имеющим собственную частоту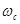 
колебаний в интервале (4…7) рад/c (вне указанного диапазона оператором либо не воспринимаются колебания, либо оператор не успевает отрабатывать отклонения от программного движения) и безразмерный коэффициент
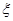демпфирования — (0,5…0,7). В связи с тем, что параметрическая идентификация относится к классу некорректных задач, всегда будет актуальной задача определения точности, полученных в результате идентификации, коэффициентов уравнения движения.
Рассмотрим эргатическую систему с уравнениями движения
,
;
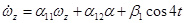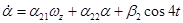(1)
(
; предполагается высокая адаптация оператора к объекту управления [1]).
При
, 
, 
,
, 
, 
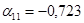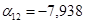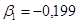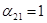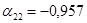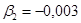
найдем решение однородной системы в форме Эйлера. Корни характеристического уравнения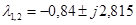 
; фундаментальная система решений имеет вид
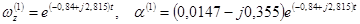
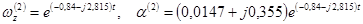
Общее решение однородной системы представится в виде:
,
.
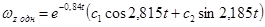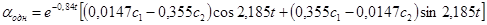Частное решение (1) имеет вид:
,
.
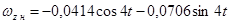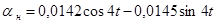При нулевых начальных условиях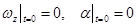 
справедливо:
,
.
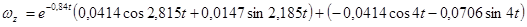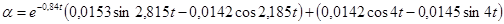(2)
Примем дискретные значения (2)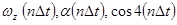 
в качестве данных нормальной эксплуатации. По ним найдем оценки коэффициентов 
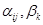. Предварительно определим оценки коэффициентов соответствующей (1) системы уравнений в конечных разностях:
,
.
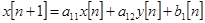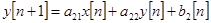(3)
Здесь принято:
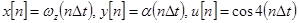. (4)
Было получено удовлетворительное совпадение указанных решений.
При регрессионном методе определение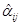 
,
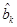сводится к выполнению условий минимума функционалов:
,
.
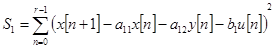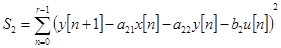Получим
,
,
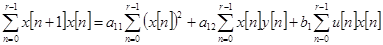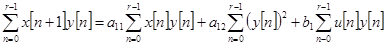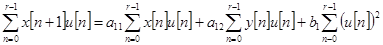(5)
,
,
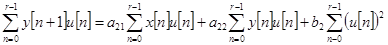. (6)
Введем
, 
, 
, 
, 
,
, 
.
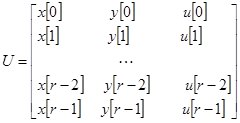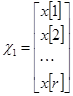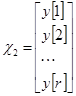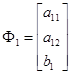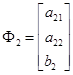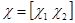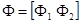Тогда параметрическая идентификация может быть осуществлена с использованием соотношения
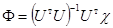. (7)
Во избежание известных неприятностей, связанных с обращением матриц, оценки коэффициентов системы (3) определяется ниже не в соответствии с (7), а непосредственно решением систем (5) и (6) (определитель системы существенно отличается от нуля) [4,5].
Введем
, 
, 
, 
,
, 
.
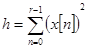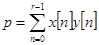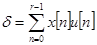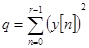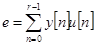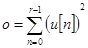Для системы (5) свободные члены уравнений равны:
, 
, 
;
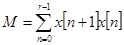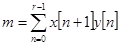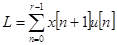для системы (6) -
, 
, 
.
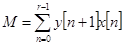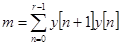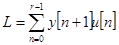Системы (5) и (6) соответственно преобразуются к виду:
, 
, 
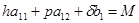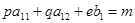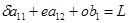; (8)
, 
, 
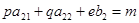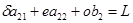. (9)
Системы (8) и (9) различаются лишь правыми частями; значения решений будут отличаться, однако алгоритмы их нахождения — одинаковые:
,
,
,
;
.
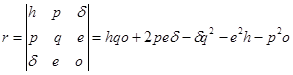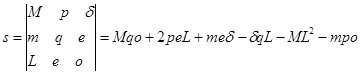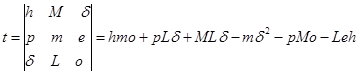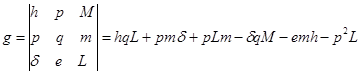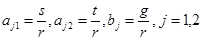Справедливы следующие соотношения:
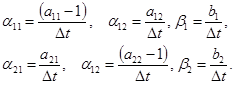
Оказалось, что ошибка определения коэффициентов не превышает 13 % (при интервале дискретизации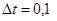 
с).
Литература:
1. Авиационные тренажеры модульной архитектуры: монография; под редакцией Лапшина Э. В., д.т.н., проф. Данилова А. М. — Пенза: ИИЦ ПГУ. — 2005. — 146 с.
2. Гарькина И.А, Данилов А. М., Пылайкин С. А. Транспортные эргатические системы: информационные модели и управление / Мир транспорта и технологических машин. — № 1(40). — 2013. — С.115–122.
3. Данилов А. М., Гарькина И. А., Домке Э. Р. Математическое моделирование управляющих воздействий оператора в эргатической системе / Вестник МАДИ. — 2011. –№ 2. — С.18–23
4. Будылина Е. А., Гарькина И. А., Сухов Я. И. Алгоритм кусочно-линейной аппроксимации с максимальным интервалом / Молодой ученый. –2014. — № 3 (62). — С. 269–271.
5. Будылина Е. А., Гарькина И. А., Данилов А. М. Приближенные методы декомпозиции при настройке имитаторов динамических систем / Региональная архитектура и строительство. — 2013. — № 3. — С. 150–156.
