Введение
Работа посвящена применению методов математической статистики к исследованию данных эксперимента с полевыми эмиссионными катодами. Целью работы является проведение анализа оценок сигнала полевой электронной эмиссии с помощью регрессионных моделей.
Автоэлектронная эмиссия обусловлена туннелированием электронов в вакуум. Это явление достигается при высокой напряженности электрического поля. Так сильное электрическое поле способствует тому, что на границе «металл — вакуум» потенциальный барьер становится достаточно тонким, что позволяет электронам проникать из твердого тела в вакуум.
Теория Фаулера-Нордгейма дает описание данного процесса, цель которого сводится к расчету плотности тока эмиссии в зависимости от электрического поля. В данной работе использована формула Фаулера-Нордгейма [1]:
(1)
где j — плотность тока, F — напряженность внешнего электрического поля, a и b — некоторые постоянные. При определенных допущениях 
и 
, где d — расстояние между электродами, а S — площадь эмиссии, формулу (1) можно привести к виду:
(2)
Задачи, поставленные перед нами:
− провести моделирование сигнала на основе двухпараметрической модели Фаулера-Нордгейма;
− построить оценки параметров модели с помощью метода наименьших квадратов для линеаризованной зависимости силы тока от напряжения;
− выполнить проверку на нормальность распределения оценок параметров линеаризованной модели с помощью критериев согласия.
- Математическое моделирование
Пусть имеются N измерений некоторого отклика 
, зависящего от фактора x и набора параметров 
. Тильда указывает, что результаты эксперимента содержат неизбежные погрешности ε. Астериск говорит о том, что компоненты вектора являются конкретными (точными) значениями параметров для данного сигнала. Предполагается существование некоторой функции 
такой, что
, i=1, 2, …, N,
причём математическое ожидание случайной величины ε равно нулю. В рассмотрение вводится регрессионная модель отклика
.
Здесь 
является функцией регрессии, которая аппроксимирует истинную зависимость . Величины 
характеризуют отклонение регрессионной модели от измеренных откликов.
Одной из целей регрессионного анализа является поиск оценки 
истинных значений параметров . Циркумфлекс показывает, что оценка обеспечивает минимум для отклонений в смысле некоторого функционала 
, т. е.
, 
,
Величины 
называют остатками регрессионной модели. Они отражают присущую отклику изменчивость и/или влияние на него неучтённых факторов.
В ходе исследования предлагается использовать функционал (метод наименьших квадратов) [2]:
, 
,
где
— весовые коэффициенты.
Оптимальный для него вектор 
обеспечивает также минимум подкоренному выражению
.
Представим связь силы тока 
с напряжением 
в виде:
. (3)
Построим линейную регрессионную модель путем преобразований:
, 
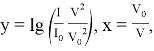
где 
, 
. Десятичный логарифм берётся для удобства (синхронизация с логарифмической шкалой). Здесь
. Соответственно определяли оценки 
и 
по формулам 
, 
.
Пусть в модели сигнала полевой эмиссии (3) значения напряжения содержат погрешности измерений, которые предлагается считать достаточно малыми 
. Величины 
могут быть учтены наряду с погрешностями измерения силы тока 
. Суммарная погрешность принимает вид:
.
В дальнейшем значения напряжения V, а значит и значения факторов x, предлагается считать измеренными точно и оперировать только безразмерной величиной ε.
В предположении малости погрешностей измерений выражение для отклика имеет вид:
,
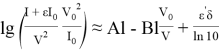где 
является стандартной нормально распределённой случайной величиной, параметр 
отвечает за т. н. уровень шума. При невысоком уровне шума можно рассчитывать на то, что в модели (3) остатки будут распределены по нормальному закону. Введем обозначение зашумленного сигнала через 
.
- Критерии согласия
Для проверки гипотезы о нормальности распределения величин использовали критерии согласия Лиллиефорса и Жака-Бера.
Критерий Лиллиефорса использует статистику вида [3]:
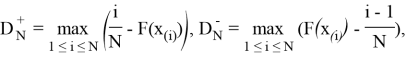
Гипотеза 
отвергается, если статистика 
превышает квантиль 
распределения статистики заданного уровня значимости α.
В тесте Жака-Бера проверяется нулевая гипотеза 
против гипотезы 
, где S — коэффициент асимметрии, который характеризует несимметричность распределения случайной величины, K — коэффициент эксцесса, являющийся мерой крутости кривой распределения. Эти коэффициенты вычисляются по формулам [4]:
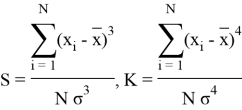
соответственно, где
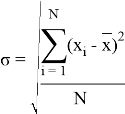
— выборочная оценка среднеквадратичного отклонения, 
— выборочное среднее, N — объём выборки.
В данном критерии используется формула [5]:
.
Полученное значение сравнивается с табличным значением распределения -квадрат с двумя степенями свободы. Если расчетное значение меньше табличного, то гипотеза принимается, выборка признается нормально распределенной. В противном случае гипотеза отклоняется.
- Численный эксперимент
В нашем случае использованы параметры 
и 
[6]. Значения напряжения 
выбраны равноотстоящими, при этом 
и 
В. Для нахождения погрешности ε использовали встроенную в MATLAB функцию, которая генерирует псевдослучайное число по нормальному закону с нулевым математическим ожиданием и средним квадратическим отклонением σ, таких экспериментов было проведено M раз.
Представлены графики зависимости значений усредненных оценок 
, 
от параметров N (рис. 1), M (рис. 2) и (рис. 3), фиксируя остальные параметры. На графиках наблюдается сходимость к истинному значению параметра B, однако для значений сходимость на всех графиках смещена ниже относительно истинного значения. При анализе поведения оценок от уровня шума наблюдалось значительное отклонение от истинного значения с ростом , что изначально и предполагалось.
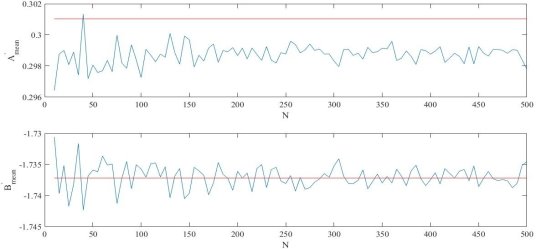
Рис. 1. Значения 
, 
при M = 100, 
для N от 10 до 500
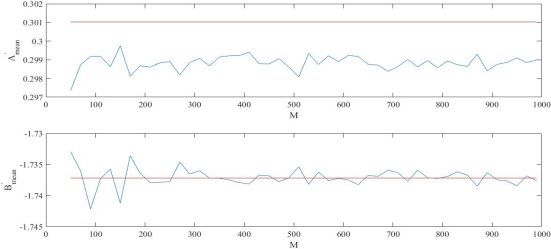
Рис. 2. Значения
, при N = 100, для M от 50 до 100
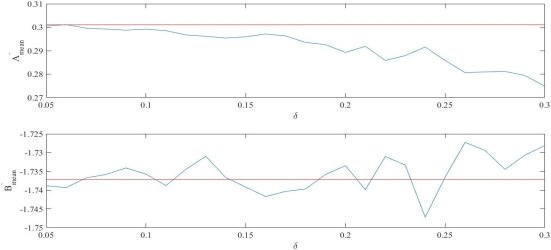
Рис. 3. Значения , при N = 100, M = 100 для 
от 5
до 30
Также была проведена проверка гипотезы о нормальности распределения оценок A и B критериями Лиллиефорса и Жака-Бера при разных значениях M, N и , в большинстве случаев нулевая гипотеза не отклоняется. Проверка статистических гипотез проводилась на уровне значимости 
. Тем не менее, анализ результатов (табл. 1) показывает, что даже большой объем выборки и малый уровень шума сигнала полевой эмиссии не гарантируют для параметров модели соответствия их закона распределения нормальному, а значит и построения доверительных интервалов классическим методом. В связи с этим возникает необходимость подбора по экспериментальным данным аппроксимирующего распределения, способного удовлетворительно описывать результаты компьютерного или натурного эксперимента.
Таблица 1
Результаты проверки на нормальность спомощью критериев Лиллиефорса иЖака-Бера
|
M |
N |
|
Лиллиефорс |
Жака-Бера |
M |
N |
|
Лиллиефорс |
Жака-Бера |
||||
|
A |
B |
A |
B |
A |
B |
A |
B |
||||||
|
100 |
10 |
0.05 |
+ |
+ |
+ |
+ |
500 |
100 |
0.05 |
+ |
+ |
+ |
+ |
|
0.1 |
+ |
+ |
+ |
+ |
0.1 |
+ |
- |
+ |
- |
||||
|
0.15 |
+ |
+ |
+ |
+ |
0.15 |
+ |
+ |
+ |
- |
||||
|
0.2 |
+ |
+ |
+ |
- |
0.2 |
+ |
+ |
+ |
+ |
||||
|
0.25 |
+ |
+ |
+ |
- |
0.25 |
+ |
- |
+ |
- |
||||
|
30 |
0.05 |
+ |
+ |
+ |
+ |
500 |
0.05 |
+ |
+ |
+ |
+ |
||
|
0.1 |
- |
+ |
+ |
+ |
0.1 |
+ |
+ |
+ |
+ |
||||
|
0.15 |
+ |
+ |
+ |
+ |
0.15 |
+ |
+ |
+ |
+ |
||||
|
0.2 |
+ |
- |
+ |
- |
0.2 |
+ |
+ |
+ |
+ |
||||
|
0.25 |
+ |
+ |
+ |
- |
0.25 |
+ |
+ |
+ |
+ |
||||
|
50 |
0.05 |
+ |
+ |
+ |
+ |
1000 |
10 |
0.05 |
+ |
+ |
+ |
- |
|
|
0.1 |
+ |
+ |
+ |
+ |
0.1 |
+ |
+ |
+ |
+ |
||||
|
0.15 |
+ |
+ |
+ |
+ |
0.15 |
+ |
+ |
+ |
- |
||||
|
0.2 |
- |
+ |
+ |
+ |
0.2 |
+ |
- |
+ |
- |
||||
|
0.25 |
+ |
+ |
- |
+ |
0.25 |
- |
- |
- |
- |
||||
|
100 |
0.05 |
+ |
+ |
+ |
+ |
30 |
0.05 |
+ |
+ |
+ |
+ |
||
|
0.1 |
+ |
+ |
+ |
+ |
0.1 |
+ |
+ |
+ |
+ |
||||
|
0.15 |
+ |
+ |
+ |
+ |
0.15 |
+ |
- |
+ |
- |
||||
|
0.2 |
+ |
+ |
+ |
+ |
0.2 |
+ |
+ |
+ |
- |
||||
|
0.25 |
+ |
- |
+ |
+ |
0.25 |
+ |
- |
- |
- |
||||
|
500 |
0.05 |
+ |
+ |
+ |
+ |
50 |
0.05 |
+ |
+ |
+ |
+ |
||
|
0.1 |
+ |
+ |
+ |
+ |
0.1 |
+ |
+ |
+ |
+ |
||||
|
0.15 |
+ |
+ |
+ |
+ |
0.15 |
+ |
+ |
+ |
- |
||||
|
0.2 |
+ |
+ |
+ |
+ |
0.2 |
- |
+ |
+ |
- |
||||
|
0.25 |
+ |
+ |
+ |
+ |
0.25 |
+ |
+ |
+ |
- |
||||
|
500 |
10 |
0.05 |
+ |
+ |
+ |
- |
100 |
0.05 |
+ |
+ |
+ |
+ |
|
|
0.1 |
+ |
+ |
+ |
+ |
0.1 |
+ |
+ |
+ |
+ |
||||
|
0.15 |
+ |
+ |
- |
+ |
0.15 |
+ |
+ |
+ |
+ |
||||
|
0.2 |
+ |
+ |
+ |
- |
0.2 |
+ |
+ |
+ |
- |
||||
|
0.25 |
+ |
+ |
+ |
- |
0.25 |
+ |
+ |
+ |
+ |
||||
|
30 |
0.05 |
+ |
+ |
+ |
+ |
500 |
0.01 |
+ |
+ |
+ |
+ |
||
|
0.1 |
+ |
- |
+ |
+ |
0.02 |
- |
+ |
+ |
+ |
||||
|
0.15 |
+ |
+ |
+ |
+ |
0.03 |
+ |
+ |
+ |
+ |
||||
|
0.2 |
+ |
- |
+ |
- |
0.04 |
+ |
+ |
+ |
+ |
||||
|
0.25 |
- |
+ |
- |
+ |
0.05 |
+ |
+ |
+ |
+ |
||||
|
50 |
0.01 |
+ |
+ |
+ |
+ |
0.06 |
+ |
+ |
+ |
+ |
|||
|
0.02 |
+ |
+ |
+ |
+ |
0.07 |
+ |
+ |
+ |
+ |
||||
|
0.03 |
+ |
+ |
+ |
+ |
0.08 |
- |
+ |
- |
+ |
||||
|
0.04 |
+ |
+ |
+ |
+ |
0.09 |
+ |
+ |
+ |
+ |
||||
|
0.05 |
+ |
+ |
+ |
+ |
0.1 |
+ |
+ |
+ |
+ |
||||
|
0.06 |
+ |
+ |
+ |
+ |
0.11 |
+ |
+ |
+ |
+ |
||||
|
0.07 |
+ |
+ |
+ |
+ |
0.12 |
+ |
+ |
+ |
+ |
||||
|
0.08 |
- |
+ |
+ |
+ |
0.13 |
+ |
+ |
+ |
+ |
||||
|
0.09 |
+ |
+ |
+ |
+ |
0.14 |
+ |
+ |
- |
+ |
||||
|
0.1 |
+ |
+ |
+ |
+ |
0.15 |
+ |
+ |
+ |
+ |
||||
|
0.11 |
+ |
+ |
- |
+ |
0.16 |
+ |
+ |
+ |
+ |
||||
|
0.12 |
+ |
+ |
+ |
+ |
0.17 |
+ |
+ |
+ |
+ |
||||
|
0.13 |
+ |
+ |
- |
+ |
0.18 |
+ |
+ |
+ |
+ |
||||
|
0.14 |
+ |
+ |
+ |
- |
0.19 |
+ |
+ |
+ |
+ |
||||
|
0.15 |
+ |
+ |
+ |
+ |
0.2 |
+ |
+ |
+ |
- |
||||
|
0.16 |
+ |
+ |
+ |
+ |
0.21 |
+ |
+ |
+ |
+ |
||||
|
0.17 |
+ |
+ |
+ |
+ |
0.22 |
+ |
+ |
+ |
+ |
||||
|
0.18 |
+ |
+ |
+ |
+ |
0.23 |
+ |
+ |
- |
+ |
||||
|
0.19 |
+ |
+ |
- |
- |
0.24 |
+ |
+ |
+ |
+ |
||||
|
0.2 |
+ |
+ |
+ |
+ |
0.25 |
+ |
- |
+ |
+ |
||||
|
0.21 |
+ |
+ |
+ |
+ |
0.26 |
+ |
+ |
+ |
+ |
||||
|
0.22 |
+ |
+ |
+ |
- |
0.27 |
+ |
+ |
+ |
- |
||||
|
0.23 |
+ |
- |
+ |
- |
0.28 |
+ |
- |
+ |
- |
||||
|
0.24 |
+ |
- |
+ |
- |
0.29 |
+ |
+ |
+ |
- |
||||
|
0.25 |
- |
+ |
- |
+ |
0.3 |
+ |
- |
+ |
- |
||||
|
0.26 |
- |
- |
- |
- |
|||||||||
|
0.27 |
+ |
- |
+ |
- |
|||||||||
|
0.28 |
+ |
+ |
- |
- |
|||||||||
|
0.29 |
+ |
+ |
- |
- |
|||||||||
|
0.3 |
+ |
+ |
+ |
- |
|||||||||
Заключение
В данной работе, используя методы регрессионного анализа, было проведено моделирование сигнала на основе двухпараметрической модели Фаулера-Нордгейма, исследована вольт-амперная характеристика для полевой эмиссионной системы и оценены параметры модели с помощью квадратичного функционала для линеаризованной зависимости силы тока от напряжения. Была выполнена проверка на нормальность распределения оценок параметров с помощью критериев согласия.
Литература:
- Fowler R. H., Nordheim L. W. Electron Emission in Intense Electric Fields // Proceedings of the Royal Society A: Mathematical, physical and Engineering Sciences, 1928. Vol. 119. № 781. P. 173–181.
- Тюрин Н. Н., Макаров А. А. Анализ данных на компьютере. М.: ИНФРА-М, 2003. 544 с.
- Lilliefors H. W. On the Kolmogorov-Smirnov test for normality with mean and variance unknown // Journal of the American Statistical Association. Vol. 62. No. 318 (Jun., 1967). P. 399–402.
- Кобзарь А. И. Прикладная математическая статистика. Для инженеров и научных работников. М.: ФИЗМАТЛИТ, 2006. 816 с.
- Jarque C. M., Bera A. K. A test for normality of observations and regression residuals // International Statistical Review. Vol. 62. No. 318, 1987. P. 163–172.
- Егоров Н. В., Антонов А. Ю., Вараюнь М. И. Анализ вольт-амперных характеристик полевого катода на основе регрессионных моделей // Поверхность. Рентгеновские, синхротронные и нейтронные исследования. 2018, № 5. С. 1–8.
