Предлагается методика определения параметров распределения управляющих воздействий оператора в эргатической системе при их различном представлении. Даются возможные приложения полученных результатов для оценки имитационных характеристик тренажных и обучающих комплексов по подготовке операторов.
Ключевые слова: эргатические системы, подготовка операторов, обучающие комплексы, имитационных характеристики, управляющие воздействия, распределение вероятностей.
Известно, психофизиологическая напряженность человека-оператора связана с параметрами объекта управления, прежде всего, собственными частотами колебаний и коэффициентами демпфирования по каждому из каналов управления. Чем лучше оператор приспособился к этим параметрам, тем меньше соответствующие амплитуды, выбросы, длительности импульсов управляющих воздействий
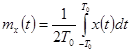 ,
,
где 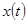 — отклонение органа управления в процессе нормальной эксплуатации (определяет программное движение). При этом
— отклонение органа управления в процессе нормальной эксплуатации (определяет программное движение). При этом
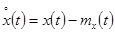 (1)
(1)
есть сигнал стабилизации программного движения, определяется как управляющее воздействие оператора. Такой подход вполне согласуется с управленческой парадигмой Мира А. Г. Бутковского. В структурной схеме целостной эргатической системы оператор представляется в виде трех звеньев. Одно из них характеризует двигательную систему человека (моторная часть), другое — формирование мысленного образа выходной координаты и, наконец, третье — центральную нервную систему, как сравнивающее устройство при формировании ошибки управления. Исходя из предыдущего, под собственными управляющими воздействиями понимаются воздействия оператора по стабилизации программного движения (флуктуации не учитываются). Естественно, определение управляющих воздействий оператора по ретроспективным данным предполагает использование итерационной процедуры.
Одной из актуальных задач является определение распределения вероятностей для различных параметров управляющих воздействий (рассматриваемых как выбросы, импульсы, непрерывные сигналы, параметры потока и т. д. [1…3]). При решении этой задачи нами использовались различные известные многосторонние критерии (предполагается отсутствие априорной информации о типе отклонения от нормального распределения).
При выборе альтернативной гипотезы: примерно симметричное распределение с убывающей кривизной или асимметричное распределение использовался критерий Шапиро-Уилка (при 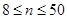 ; при
; при 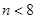 достоверность отклонения от нормального распределения не гарантируется). В этом случае используются
достоверность отклонения от нормального распределения не гарантируется). В этом случае используются 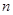 независимых упорядоченных наблюдений
независимых упорядоченных наблюдений 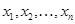 (значения не убывают)
(значения не убывают)
Сначала вычислялась сумма
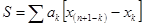 ;
; 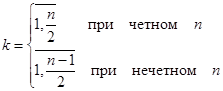 ,
,
коэффициенты 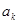 определяются по заданному объему выборки
определяются по заданному объему выборки 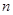
Статистика критерия 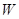 имеет вид:
имеет вид:
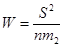 ,
,
где 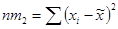 ;
;
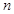 — объем выборки;
— объем выборки;
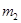 — выборочный центральный момент второго порядка (выборочная дисперсия).
— выборочный центральный момент второго порядка (выборочная дисперсия).
Критическая область критерия при уровне значимости 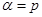 образуется значениями, меньшими, чем
образуется значениями, меньшими, чем 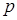 -квантиль для
-квантиль для 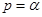 .
.
В случаях 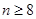 по
по 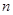 наблюдениям
наблюдениям 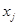
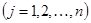 определялись:
определялись:
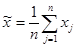
и
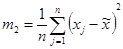 ,
,
где 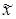 — среднее арифметическое;
— среднее арифметическое;
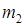 - выборочный центральный момент второго порядка;
- выборочный центральный момент второго порядка;
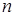 — объем выборки.
— объем выборки.
Вычислялась статистика критерия 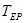 Эппса-Палли
Эппса-Палли
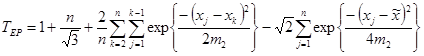
в соответствии с приводимым алгоритмом:
- задание объема выборки 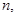
- определение всех значений выборки 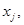
- вычисление среднего арифметического 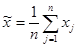 ,
,
- определение центрального момента 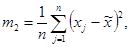
- вычисление 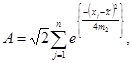
- вычисление 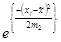 ;
; 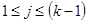 ,
,
- вычисление 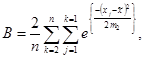
- вычисление статистики 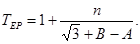
Если при данном уровне значимости 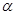 и объеме выборки
и объеме выборки 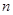 вычисленное значение статистики
вычисленное значение статистики 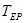 превышает
превышает 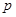 -квантиль, то нулевая гипотеза отклоняется.
-квантиль, то нулевая гипотеза отклоняется.
Были получены важные выводы о распределении вероятностей параметров управляющих воздействий. В частности, мгновенные амплитуды управляющих воздействий, рассматриваемых как непрерывные процессы, можно считать распределенными нормально (непосредственно следует и из центральной предельной теоремы). Если управление рассматривать как импульсный процесс, то гипотеза о нормальном распределении амплитуд импульсов должна быть отвергнута.
Очевидны приложения такого подхода к управляющим воздействиям оператора к разработке тренажных и обучающих комплексов различного назначения, особенно, для систем на подвижном основании. В описательной части оценка качества имитационных характеристик таких комплексов сводится к сравнению управляющих воздействий оператора в условиях модели и реального объекта. Но до сего времени не отработана методика сравнения. Исключение составляет лишь компенсирующее отслеживание, когда оператор наблюдает только рассогласование между входом и выходом и стремится уменьшить это рассогласование до нуля. С определенной оговоркой это имеет место и для преследующего отслеживания, когда оператору предъявляется независимо и входной и выходной сигналы, и оператор стремится их совместить.
Нами управляющие воздействия определялись ретроспективно по данным нормального функционирования. Это позволило не только производить формализованную оценку привития навыка управления, качества управления, а также качества обучающего комплекса с построением структурной схемы для самого распространенного режима стабилизации программного движения. При квазилинейной модели оператора схема приводится к одноконтурной системе автоматического управления. Ее параметрическая идентификация может быть произведена итерационным методом с последовательным уточнением параметров, как объекта, так и оператора.
Оценка имитационных характеристик обучающих комплексов, естественно, требует сопоставления субъективной оценки оператором качества модели по совокупности объективных показателей. Это задача принципиально всегда может решаться на основе классификации систем уравнений движения и использовании специально разработанных функционалов качества [4…6].
Литература:
1. Будылина Е. А., Гарькина И. А., Данилов А. М., Махонин А. С. Основные принципы проектирования сложных технических систем в приложениях / Молодой ученый. — № 5. 2013. –С.42–45.
2. Гарькина И. А., Данилов А. М. Управление в сложных технических системах: методологические принципы управления / Региональная архитектура и строительство. –2012. — № 1 (12). — С.39–43.
3. Данилов А. М., Гарькина И. А. Теория вероятностей и математическая статистика с инженерными приложениями: учебное пособие. — Пенза: ПГУАС. — 2010. — 228 с.
4. Гарькина И.А, Данилов А. М., Пылайкин С. А. Транспортные эргатические системы: информационные модели и управление / Мир транспорта и технологических машин. –2013. –№ 1(40). –С.115–122.
5. Гарькина И. А., Данилов А. М., Домке Э. Р. Промышленные приложения системных методологий, теорий идентификации и управления / Вестник МАДИ. — 2009. — № 2(17). — С.77–82.
6. Будылина Е. А., Гарькина И. А., Данилов А. М. Приближенные методы декомпозиции при настройке имитаторов динамических систем / Региональная архитектура и строительство. — 2013. — № 3(17). — C. 150–156.







