Компьютерные тесты самой разнообразной направленности приобретают всё более широкое распространение. Здесь будем рассматривать анимационные психологические тесты. В процессе тестирования испытуемый даёт свою трактовку того, что он видит, выбирая из заданного множества вариантов. Например, тестовая анимация — вращающаяся танцовщица. Варианты трактовки: она вращается по часовой стрелке, она вращается против часовой стрелки. Другой пример — крутящееся колесо, варианты трактовки те же. Объекты могут совершать переход к другому типу движения, что является оптической иллюзией. Результатом тестирования является динамический ряд возникающих трактовок. По тому, как трактовка изменяется во времени, предлагается судить о доминирующем полушарии. Мы попытаемся предложить метод математического анализа данных тестирования, который по результатам тестирования даёт обоснованную классификацию испытуемых. Для решения этой задачи следует рассмотреть абстрактную модель процесса. Представим мозг, воспринимающий дискретный поток кадров, как автомат, обеспечивающий решение математической задачи. Выполняя многовариантную манипуляцию, автомат порождает модельный поток кадров, который является буфером между реальным потоком и всем, что связано с выполнением психических функций в результате наблюдения и в связи с ним. Этот автомат будем здесь называть мозгом, подразумевая именно такую модельную абстракцию. В целях разработки математического метода необходимо сделать следующее: а) формализовать феномен восприятия, предложив алгоритм элементарных действий как модель процесса; б) сформулировать предположение о специфике восприятия при разных типах полушарного доминирования в категориях абстрактной модели процесса восприятия; в)составить математическую модель восприятия анимации и провести эксперимент с целью статистической проверки гипотез, на которых основывается модель процесса восприятия; г) предложить метод анализа данных, собранных при тестировании испытуемых, для классификации испытуемых по типу доминирования полушария.
Всё время, пока идёт смена кадров реального потока, мозг ритмично генерирует модельный аналог, Кроме того, в том случае, если пройден установленный интервал, называемый в дальнейшем интервалом восприятия, он осуществляет контроль точности восприятия, сопоставляя модель с прототипом. Это сопоставление может вызвать действия, которые следуют из результатов этого сопоставления, например, изменение трактовки и создание соответствующей оптической иллюзии, или его результаты просто запоминаются.
Как известно, люди с доминирующим правым полушарием более склонны к образному мышлению. В отличие от логического мышления, законы образного мышления не формализованы. Такое мышление — интуитивный процесс, отличающийся внезапным обнаружением истины, всплывающей из глубин подсознания. Нам кажется, что процесс образного мышления можно представить как множество квазигармонических колебаний, происходящих одновременно. В то же время сама компьютерная анимация есть одновременное существование разнообразных колебаний, ритмов появления отдельных кадров, невозможность предсказания кадра означает большую или меньшую неопределённость объекта восприятия. Неопределённость в информатике принято измерять энтропией, или количеством информации, которое несёт сообщение или их совокупность. Если у человека развитое образное мышление, то от него можно ожидать отличий в процессе ритмического восприятия анимации, которая сама есть ритмическая смена кадров.
Рассмотрим подробнее упомянутый выше анимационный ролик “Вращающаяся танцовщица” (http://en.wikipedia.org/wiki/Spinning_Dancer), повторим, что на нём балерина вращается вокруг своей оси. Почти каждый кадр, а всего их 34, позволяет две трактовки. В результате балерина движется по часовой стрелке и против часовой стрелки одновременно. Однако есть несколько кадров, которые прямо указывают на одну трактовку. При этом в пользу движения по часовой стрелке и левой опорной ноги мы обнаружили признаки в 6-ти кадрах, а в пользу альтернативной трактовки говорят детали в одном 13-м кадре [1]. Мы провели эксперименты с роликами двух типов. В первом ролике в части анимации не было изменений в оригинале. В ролике второго типа были выбраны из имеющихся ещё дополнительные кадры числом от 4 до 6, в которые были внесены изменения в виде крошечных штрихов, создающих пространство и указывающих на то, что балерина стоит на правой ноге. Теперь два возможных варианта сопоставления стали почти равновероятны. Оба ролика давали возможность, кликая на соответствующей кнопке, фиксировать испытуемому, что и когда он видит. Результаты первичной статистической обработки собранных данных представлены в таблице 1. В ней M(X) — математическое ожидание случайной величины X, T — продолжительность наблюдения до первого изменения трактовки, выраженная в циклах анимации, L –общая продолжительность наблюдения, d — интервал между изменениями трактовки, n — число изменений трактовки в одном эксперименте.
Таблица 1
Результаты экспериментов
|
Тип ролика– число наблюдений |
Параметры анимации |
H0 |
Статистики | ||||
|
p1 |
p2 |
M(T) |
M(L) |
M(d) |
M(n) | ||
|
1–13 |
1/7 |
6/7 |
0,28 |
70 |
196 |
29 |
4 |
|
2–13 |
6/11 |
5/11 |
0,48 |
41 |
158 |
24 |
5 |
Статистический анализ показал, что очень многие статистические показатели изменились не значимо. Главные изменения коснулись величины T. Основываясь на характере изменений, выскажем гипотезу о том, почему время до первого изменения трактовки сократилось, и предложим математическую модель процесса восприятия. Время до изменения трактовки стало меньше, потому что стала больше неопределённость каждого информационного сообщения в момент сопоставления модельного аналога и реального прототипа. Как только накопленная энтропия превышает порог, мозг начинает корректировать свой модельный аналог, как бы стирая накопленную энтропию и “начиная сначала”. Это предельное значение накопленной энтропии дискретно уменьшается с течением времени, поэтому в среднем интервал до следующего изменения трактовки сокращается. Общая практика такова, что нужно дождаться первого поворота балерины, а дальше она будет поворачиваться “легче” и можно досмотреть до того, что балерина начнёт прыгать с ноги на ногу, так что за этим движением едва успевает глаз. Частота создания оптических иллюзий тоже может быть ограничена мозгом, поэтому можно наблюдать, как люди с правополушарным доминированием почти сразу же видят поворот и очень быстро хотят прекратить эксперимент. Можно предположить, что правополушарные люди видят чаще вращение, которое начинается движением с правой опорной ноги, и вообще раньше видят поворот потому, что обладают вызванным склонностью к образному мышлению свойством допускать большую степень неопределённости информационного сообщения. Они учитывают циклическое появление в разных кадрах еле заметных признаков трактовок, но ограничены той же величиной накопленной энтропии, или ещё меньшей, поэтому предел накопленной энтропии наступает раньше и они раньше начинают делать корректировку текущей трактовки.
Запишем высказанные выше предположения в математической форме. Итак, суммарная накопленная энтропия восприятия до первой корректировки имеет следующую форму зависимости:
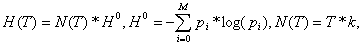 (1)
(1)
где T — время наблюдения, M — число трактовок, pi — вероятность того, что случайный кадр в пределах цикла содержит информацию в пользу i-й трактовки, k — коэффициент пропорциональности, величина которого зависит от интервала между сопоставлениями. Величину H0 будем называть энтропией сопоставления. Покажем, что экспериментальные данные не противоречат модели (1). Если изменение величин pi приводит к изменению H0 до уровня H02, а H(T) изменяется на a, то величину b, на которую изменяется k, можно определить по формуле:
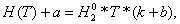 (2)
(2)
При a=0, т. е. при условии стабильности H(T) формула (2) преобразуется к виду:
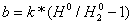 (3)
(3)
Сопоставим с экспериментальными данными. После внесения дополнения в ролик, во 2-м эксперименте время наблюдения до корректировки M(T) составило 0,6 от аналогичного значения в первом эксперименте. Отсюда b=-0,4k. В то же время, поскольку наблюдённые значения H0 и H02 составляют соответственно 0,28 и 0,48, то из формулы (3) получаем b=k*(0,28/0,48–1)=-0,42k.
Теперь рассмотрим период после первого изменения трактовки. Экспериментальные данные говорят о том, что и здесь сохраняется прежняя логика — чем меньше энтропия сопоставления, тем больше интервал между изменениями трактовок. Статистический анализ показал, что величина d симметрично группируется вокруг своего математического ожидания и при большем размере выборки можно было бы проверить гипотезу о нормальном распределении этой величины, но при этом само математическое ожидание для каждой энтропии сопоставления таково, чтобы произведение его на энтропию сопоставления не изменялось и сохранялось относительно стабильным. Продолжительность наблюдения за роликом, которая была произвольной, на усмотрение испытуемого, не зависела от энтропии сопоставления и менялась очень мало, при этом различалось число изменений трактовок в процессе наблюдения. Вопрос о том, какая из этих двух величин является причиной, а какая следствием, требует дальнейшего исследования. Обозначим через de — средний интервал между изменениями трактовки при проведении эксперимента с энтропией сопоставлений He0, величина He0 определяется по кадрам анимации и формуле (1), d0 — средний интервал для эталонного в отношении энтропии сопоставлений ролика и заданной психологической характеристики.
Поскольку M(d0)/M(de)=He0/H0, то количество изменений трактовки на момент времени T0 Y(T0) равно:
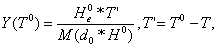 (4)
(4)
Формулы (1)-(4) являются математической моделью процесса восприятия тестового ролика.
Рассмотрим теперь, как применить модель для классификации испытуемых по типу полушарного доминирования. Нам кажется вполне вероятным предположение, что испытуемые с лево- и правополушарным доминированием будут иметь собственные величины M(d0) и H0 для каждого ролика тестовой анимации. Если определить их значения на контрольной выборке, то вероятность принадлежности к конкретному типу для испытуемого будет равна вероятности принадлежности наблюдённой величины Y(T0) генеральной совокупности с параметрами, присущими тому или иному полушарному доминированию.
С нашей точки зрения, математический подход к оценке психологических характеристик расширяет возможности практического применения компьютерных анимационных тестов и увеличивает их прикладную и теоретическую ценность. В этой связи задача математического моделирования связанных с анимацией когнитивных процессов представляется актуальной и перспективной.
В заключение мы выражаем благодарность Тиндарей Л. И. за помощь в сборе экспериментальных данных.
Литература:
1. Клименко, А.О. — Модель процесса восприятия компьютерной анимации/А. О. Клименко // Естественно-гуманитарные исследования.-2014.-№ 3(5).- С.141–146.

