Введение
Идея создать универсальную программно-алгоритмическую реализацию метода роя частиц возникла при исследовании его эффективности применительно к одной из NP — трудных задач. Требовалось проводить множество испытаний с различными параметрами и модификациями, при этом каждая новая версия требовала пересборки программы. В связи с этим возникла идея разбить исходную задачу на модули, вынеся взаимозаменяемые функциональные части в отдельные компоненты, что значительно упростило бы разработку модификаций и исследование различных их сочетаний.
Метод роя частиц
Метод роя частиц был предложен в 1995 году Джеймсом Кеннеди (James Kennedy) и Расселом Эберхартом (Russel Eberhart) для оптимизации нелинейных функций [5]. Метод моделирует многоагентную систему, где агенты-частицы двигаются к оптимальным решениям, обмениваясь при этом информацией с соседями.
В методе роя частиц каждое потенциальное решение представлено точкой в поисковом пространстве, называемой частицей. Алгоритм метода роя частиц представляет итерационный процесс, который продолжается до тех пор, пока не будет выполнен критерий остановки. Такими критериями, например, могут быть достижение предельного числа итераций, достижение определенного значения целевой функции, сходимость алгоритма.
На первом шаге алгоритма создается множество решений, называемое популяцией. Положение i-й частицы на итерации t характеризуется D-мерным вектором координат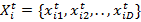 
и вектором скорости 
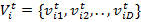, где D — размерность пространства решения. Кроме обмена информацией с соседями каждая частица помнит собственное наилучшее положение, т. е. обладает памятью. На каждой итерации алгоритма направление и длина вектора скорости каждой из частиц в классическом алгоритме изменяются в соответствие со сведениями о найденных оптимумах [5]:
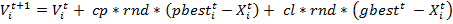(1),
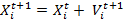(2),
где cp,cl — коэффициенты ускорения частицы, отражают стремление частицы достигнуть глобально лучшего решения, либо сохранить свое;
rnd -случайное число из интервала [0;1];
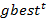— координаты лучшего решения роя, достигнутого к t-й итерации;
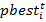— координаты лучшего решения, достигнутого i-й частицей к t-й итерации.
Выражение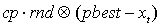 
также называют когнитивным компонентом. Он определяет производительность частицы по отношению к прошлым результатам и выступает в роли индивидуальной памяти о наиболее оптимальной позиции данной частицы. Посредством этого компонента, частица может возвращаться в состояния, которые были наилучшими для нее в прошлом [2].
Выражение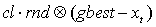 
называют социальным компонентом, определяет производительность частицы по отношению к соседним. Благодаря ему частица имеет возможность передвигаться в оптимальные позиции, которые были найдены соседними частицами, исследуя при этом окружающее пространство [2].
Для повышения качественных характеристик алгоритма в выражение (1) вводится коэффициент инерции w, показывающий, какую долю начальной скорости сохранит частица. Посредством этого коэффициента можно регулировать сходимость алгоритма, большие значения способствуют разлету частиц, маленькие — тщательному исследованию окрестностей частицы, целесообразно постепенное уменьшение коэффициента, благодаря этому на первых этапах работы алгоритма более равномерно распределятся по пространству поиска, а на поздних обеспечит хорошую сходимость [3].
Кроме того, использование глобально лучшего решения gbest в формуле (1) может привести к быстрой сходимости в некоторый локальный оптимум, поэтому компонент gbest заменяется на lbest, означающий лучшее решение среди некоторого множества других частиц — соседей. Таким образом, (1) примет вид:
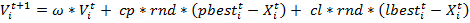(3)
Пример одного шага работы алгоритма представлен на рисунке 1 [2], процесс поиска в течение нескольких итераций для некоторой функции с минимумом в точке (0,0) на рисунке 2 [1].
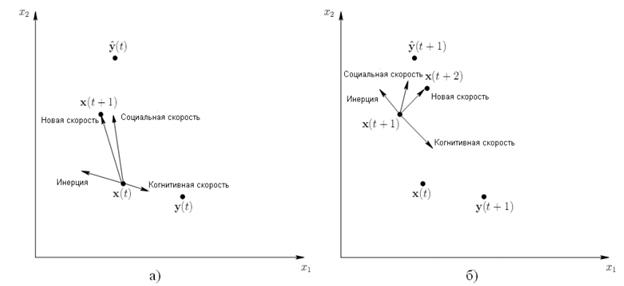
Рис. 1. Иллюстрация одного шага метода роя частиц а) момент времени t б) момент времени t+1
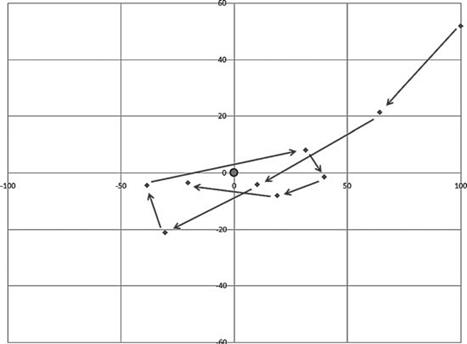
Рис. 2. Иллюстрация траектории одной частицы на примере функции с оптимумом в точке (0;0)
Программно-алгоритмическая модель
В процессе исследования алгоритма возникла задача разработки каких — либо модификаций. Внесение любого изменения требовало перекомпиляции всей программы, т. к. система роя частиц была монолитной. Для решения этой проблемы задача была разбита на отдельные этапы, модули, выполняющие ограниченный функционал.
Применительно к некоторому классу численных итеративных методов оптимизации можно выделить следующие компоненты:
- Метод решения;
- Критерий завершения;
- Оптимизируемая задача;
- Решатель.
Рассмотрим каждый из компонентов по отдельности:
Метод решения — выполнение одного шага алгоритма, в соответствии с заданным методом. Как правило, одновременно оперирует множеством решений;
Критерий завершения — условие завершения расчетов, например достижение некоторого числа итераций, достижение требуемого значения целевой функции, отсутствие новых решений в течение длительного промежутка времени (в случае, если алгоритм сошелся);
Оптимизируемая задача — описывает процедуру расчета значения целевой функции в заданной точке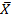 
пространства 
;
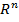Решатель — производит поиск решения согласно заданным критерию завершения, искомой задаче и методу решения.
Диаграмму, связывающую компоненты можно представить схемой, изображенной на рисунке 3.
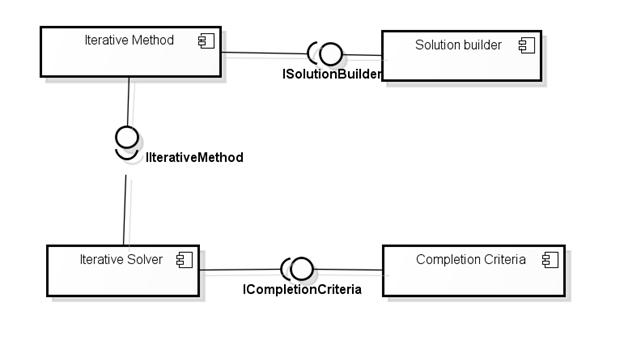
Рис. 3. Схема некоторого абстрактного решателя
Алгоритм работы системы представлен на рисунке 4.
В соответствии с данным алгоритмом и структурной схемой, выделим основные функции, выполняемые компонентами решателя:
Метод решения:
- Start Action — инициализация, создание популяции решений;
- Iteration — выполнение одного шага алгоритма согласно заданному методу;
- Final Action — освобождение используемых ресурсов;
- Initialize — инициализация метода, передача объекта — декодера решения, оценивающего по вектору координат 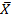значение целевой функции F;
- GetBestSolution — возврат лучшего найденного решения, необходим для передачи пользователю данных о найденном оптимуме.
Критерий завершения:
- Check — проверка достижения заданного критерия остановки алгоритма;
- Abort — вызов принудительной остановки алгоритма. Следующий за Abort вызов функции Check вернет true;
- Reset — сброс достигнутого прогресса для критерия завершения (например обнуление числа итераций). Следующий за Reset вызов функции Check вернет false.
- Решатель:
- GetSolution — получение найденного решения;
- Initialize — инициализация решателя;
- Run — запуск вычислений.
Декодер решения:
- GetFitness — оценка решения, представляемого вектором ;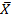
- GetDimSize — размерность пространства решения.
Описанная схема классов представлена на рисунке 5.
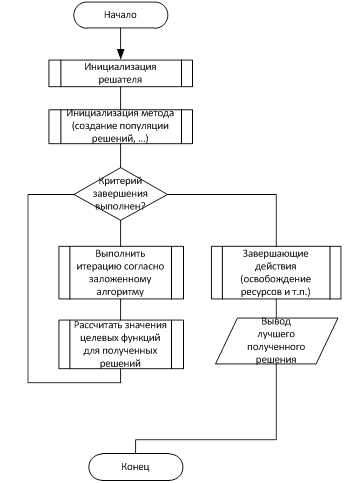
Рис. 4. Обобщенный алгоритм работы итеративного решателя
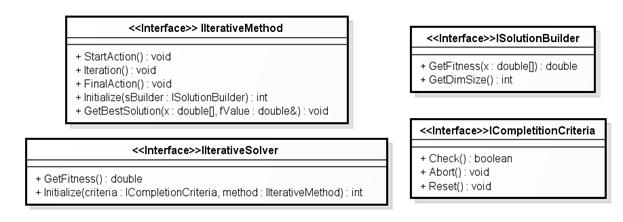
Рис. 5. Схема классов решателя
В данной работе в качестве метода решения рассматривается метод роя частиц. Ему присущи свои особенности, поэтому остановимся подробней на реализации интерфейса IIterativeMethod. Известно множество вариаций МРЧ. Выделим основные направления модификаций:
1) Выбор параметров — определение параметров cp, cl, w для каждой частицы. Параметры могут задаваться как константами, так и меняться в процессе работы, например, было показано, что уменьшение коэффициента W улучшает поисковые способности алгоритма [3], кроме того, возможны варианты с адаптивной настройкой алгоритма под текущий класс задач/текущий экземпляр задачи.
2) Отношения соседства — не менее важный компонент МРЧ, от него напрямую зависит сходимость алгоритма. Реализация этого компонента позволит на одном экземпляре МРЧ исследовать различные топологии соседства (клика, тора, кластерные [3,4]), а также проводить кластеризацию решений по другим признакам (например, эвклидово расстояние, по распределению качеств решений).
3) Расчетная формула — известно множество модификаций метода, имеющих разный подход к определению векторов скорости и координаты частицы. Производит преобразование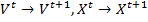 
, где V,X — вектора скорости и координат частицы, t — номер итерации.
Очевидно, что частица не может самостоятельно управлять ни выбором своих параметров, ни выбором соседей, т. к. ей не хватает информации об окружающем пространстве. Поэтому для пунктов 1–2 целесообразно создать двухуровневую структуру, первый уровень — управляющий, второй — реализующий свою функцию с учетом информации, предоставленной 1м уровнем. В итоге получаем схему, представленную на рисунке 6.
Видно, что при таком подходе, частица выступает только в роли контейнера — хранит требуемую информацию, поведение предопределено реализацией других модулей, начиная от видимости других частиц — списка соседей, и заканчивая использованием этой информации для перемещения в другую точку.
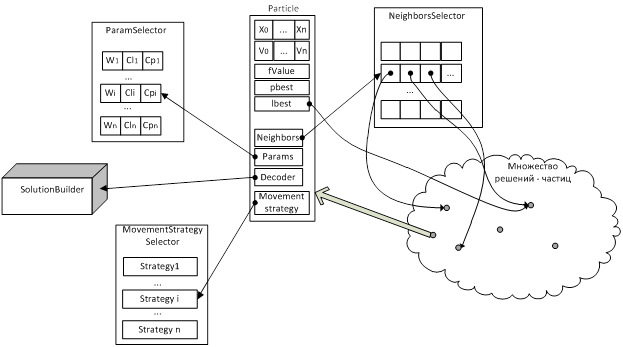
Рис. 6. Схема организации метода роя частиц
Селекторы выполняют управлением массивом предоставленных им данных, в зависимости от текущей ситуации (распределение частиц в пространстве решений, текущей итерации и т. п.) и заложенной стратегии. Для этого они реализуют 2 функции:
- Initialize(_partArray:Particle [], _size: const int) — первоначальная настройка селектора, привязка стратегий, параметров, функционала к частицам;
- Update() — обновление внутреннего состояния селектора, адаптация к внешним условиям. По умолчанию выполняется на каждой итерации.
Такой подход практически не ограничивает разработчика в реализации различных сценариев, так, посредством реализации адаптивного, самонастраивающегося ParamSelector'а можно добиться подстройки МРЧ практически под любой класс задач без дополнительного вмешательства разработчика. Реализация разных стратегий перемещения частицы позволяет присваивать частицам различные роли, что добавляет методу гибкости. С помощью NeighborsSelector'а возможен контроль сходимости алгоритма путем изменения числа связей между частицами, возможна динамическая смена топологий соседства.
Литература6
1. Маккаффри Д. Искусственный интеллект: Метод роя частиц // Журнал MSDN Magazine Август 2011
2. Субботин С. А., Олейник Ан.А., Олейник Ал.А. Интеллектуальные мультиагентные методы. Часть III// Фрагменты рабочих материалов монографии
3. Карпенко А. П., Селиверстов Е. Ю. Обзор методов роя частиц для задачи глобальной оптимизации (Particle Swarm Optimization) //Наука и образование. 2009. вып. 03. URL: http://technomag.edu.ru/doc/116072.html (Дата обращения: 01.05.2013)
4. Антух А. Э. Исследование канонического метода роя частиц (PSO) для топологий типа «клика» и «кластер» // Наука и образование. 2009. вып. 06. URL: http://technomag.edu.ru/doc/127975.html (Дата обращения: 01.05.2013)
5. Kennedy J., Eberhart R. Particle Swarm Optimization — Proceedings of IEEE International Conference on Neural Networks IV. — 1995. — С. 1942–1948.
