Приводятся практическая реализация методов планирования эксперимента при составлении аппроксимационной модели функций многих переменных.
На уровне экспериментальных исследований коэффициенты определяются согласно принципа разложения функции выходной координаты (следствия) в ряд Тейлора в окрестности рабочей точки по набору входных координат (причин) [1]. За координаты рабочей точки — принимаются регламентные значения тех технологических переменных, которые определяют режим нормальной эксплуатации технологического объекта. При разложении же в ряд Тейлора — согласно принципа линеаризации — обычно используются только линейные (первые) члены этого разложения.
Принцип линеаризации является современным базовым принципом преставления модели технологического процесса для целей управления этим процессом. Так как считается, что в процессе нормальной эксплуатации — за счет процесса работы систем управления — отклонения от рабочей точки работы объекта для его режима нормальной эксплуатации
- либо не выходят за пределы линейности,
- либо можно пренебречь вкладом от имеющихся нелинейностей.
Указанное выше можно проиллюстрировать графически. Так для выходных переменных РВЫХ и QВЫХ в представленном примере их общие неявные зависимости от входных переменных F, R и QВХ могут быть представлены в виде:
РВЫХ = Ф1 (F, R, QВХ) (1)
QВЫХ = Ф2 (F, R, QВХ) (2)
Тогда согласно линейного разложения в ряд Тейлора внутри областималых отклонений  (приращений) для входных координат (при работе систем автоматического управления) можно записать для
(приращений) для входных координат (при работе систем автоматического управления) можно записать для  РВЫХ и
РВЫХ и  QВЫХ:
QВЫХ:
 РВЫХ = (
РВЫХ = (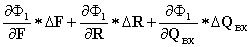 ) (3)
) (3)
 QВЫХ = (
QВЫХ = (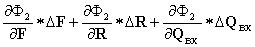 ) (4)
) (4)
В выражениях (3) и (4) частные производные соответствуют искомым коэффициентам:
К12 = 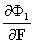 ; К22 =
; К22 = 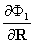 ; К32 =
; К32 = 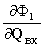 ; (5)
; (5)
К13 = 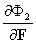 К23 =
К23 = 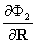 К33 =
К33 = 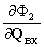 . (6)
. (6)
Эти частные производные (или коэффициенты) находятся как соответствующие касательные к рабочей точке режима нормальной эксплуатации. Рабочая точка и диапазон режима нормальной эксплуатации должны быть представлены на статической характеристике для выбранного KIJ канала преобразования информации (рисунок 1).
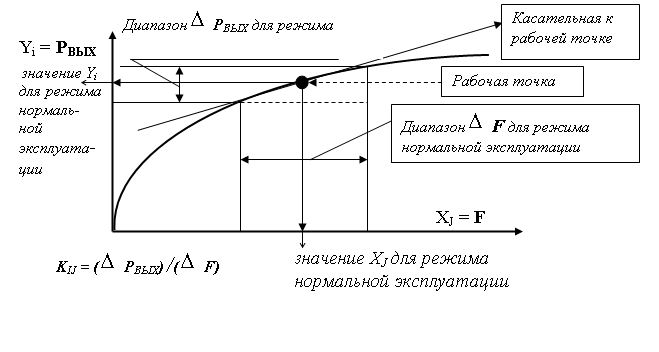
Рис. 1. Статическая характеристика технологического процесса
Определение полного набора KIJ для технологической установки обычно осуществляется широко распространенным методом планирования экспериментов путем выявления и построения уравнения регрессии [2]. В простейшем случае эти уравнения регрессии представляются в форме линейных уравнений типа (3)и (4).
Форма этих уравнений соответствует линейной аппроксимации нелиненейных статических характеристик в области рабочего диапазона нормальной эксплуатации установки процесса.
Литература:
1. Иванилов Ю. П., Лотов А. В. Математические модели в экономике.- М.: “Наука”, 1989.
- Бергстром А. Построение и применение экономических моделей. — М.: “Прогресс”, 1970.
- Тотьменинов М.Е. Информационно-технологические схемы и модели технологических установок и процессов. Учебно-методическое пособие. - Томск: Изд. ТПУ, 2000 – 52с.: ил. 38.
4.

