Исследование методической погрешности метода квазиэквивалентного укрупнения состояний марковских моделей



В предыдущей статье «Принцип квазиэквивалентного укрупнения состояний марковских моделей» мы выяснили, что при квазиэквивалентном укрупнении выходные характеристики N_ср (среднее число заявок в системе «процессоры-каналы») и M [t_р] (среднее время реакции системы ) системы ведут себя закономерно — увеличиваются с ростом λ (интенсивность поступления заявок) и уменьшаются с ростом μ (интенсивность обслуживания). Следовательно, метод квазиэквивалентного укрупнения заслуживает более детального изучения, в особенности его методической погрешности и её влияния на итоговый результат работы АИС.

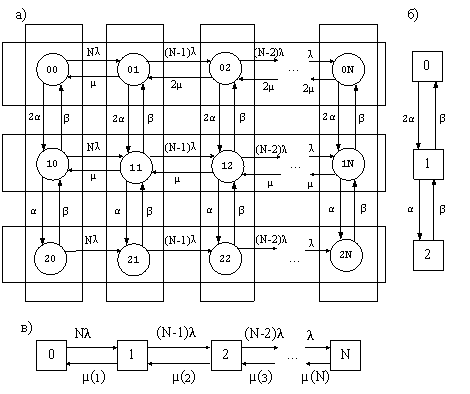
Рис. 1. Графы переходов для двухпроцессорной системы: а) граф исходного процесса; б) граф процесса с эквивалентным укрупнением состояний; в) граф процесса с квазиэквивалентным укрупнением состояний

Для нахождения точного решения СЛАУ, описывающих состояния вероятностного графа, изображённого на рис. 1, прибегнем к методу итераций. Для этого сначала составим уравнения Колмогорова для всех состояний этого графа.

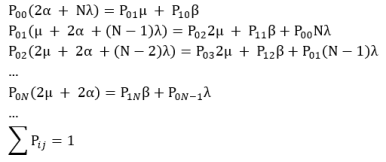(1)

Преобразуем (1).

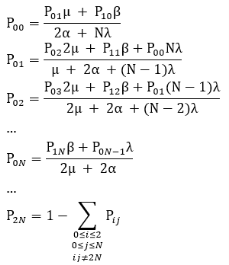(2)

За нулевое приближение примем значения вероятностей, вычисляемых согласно допущению , где 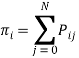, 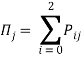. Следовательно, первое приближение будет иметь следующий вид:

Второе и последующие приближения будет выглядеть аналогично (3). В общем виде уравнения будут выглядеть так:

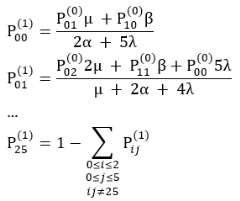(3)

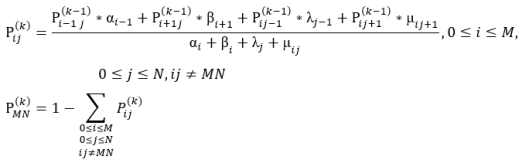(4)

где α_i = (M-i)*α, β_i =, λ_j = (N-j)*λ,

Во время выполнения каждой итерации будем подсчитывать разности значений и вычислять максимум из них. Кроме того, будем анализировать погрешность выходных значений N_ср, M [t_р], M_ср, вычисленных при помощи метода квазиэквивалентного укрупнения (нулевая итерация) и точным методом (финальная итерация). Возьмём T_отк = 100, T_восст = 10, T_обд = 10, T_реш = 5. Построим график зависимости для системы с заданными характеристиками:

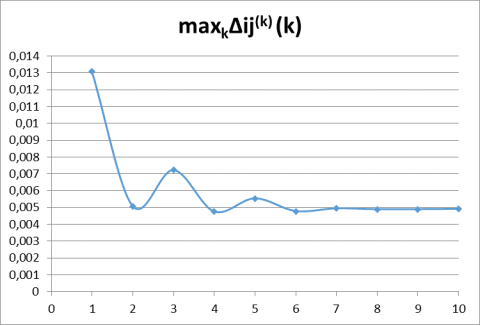
Рис. 2. График зависимости при N=5, M=2 и 10 итерациях

Как видим, при заданных входных параметрах динамика значений максимальных разностей меняется крайне скачкообразно на начальных итерациях. Значения N_ср, M [t_р] и M_ср для метода квазиэквивалентного укрупнения соответственно равны 2,143, 7,503, 1,803, для точного метода — 2,173, 7,686, 1,808. Погрешности их значений составляют 1,38 %, 2,44 % и 0,28 % соответственно. Но что будет, если увеличить количество итераций до 100?

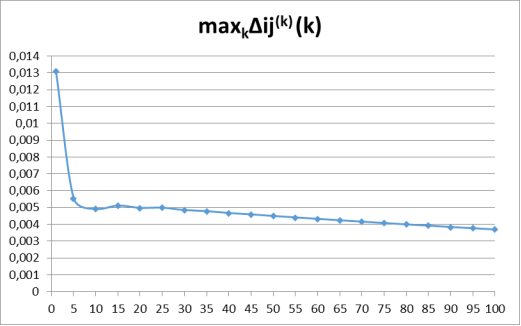
Рис. 3. График зависимости при N=5, M=2 и 100 итерациях

Ситуация улучшилась — значения на последующих итерациях стали плавно уменьшаться. Значения N_ср, M [t_р] и M_ср для точного метода при 100 итерациях соответственно равны 2,19, 7,796, 1,803, а их погрешности — 2,2 %, 3,91 % и 0,02 %. Проверим состояние графика при 1000 итераций.

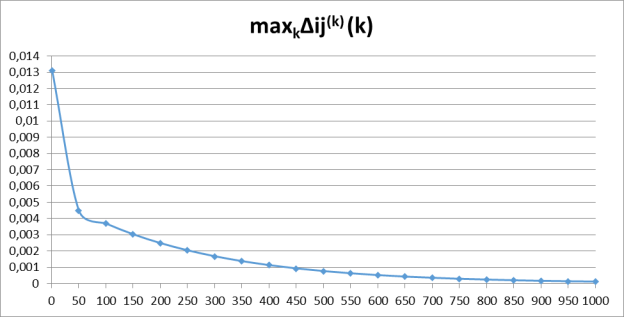
Рис. 4. График зависимости при N=5, M=2 и 1000 итераций

На 1000 итераций значения выходных характеристик для точного метода составляют 2,19, 7,794, 1,803, а их погрешности — 2,18 %, 3,88 % и 0 %. При дальнейшем увеличении числа итераций N_ср, M [t_р] и M_ср для точного метода сохраняют данные значения. Так или иначе, для рассматриваемой системы метод квазиэквивалентного укрупнения однозначно сходится.

Рассмотрим более обширную систему. Возьмём N=30, M=5. Значения T_отк, T_восст, T_обд и T_реш оставим прежними. Число итераций сразу поставим равным 1000.

Рис. 5. График зависимости при N=30, M=5 и 1000итерациях

Метод сходится гораздо быстрее, чем для системы с меньшим числом терминалов и процессоров, а значения N_ср, M [t_р] и M_ср для точного и квазиэквивалентного метода совпадают: 21,279, 24,4 и 4,36.

Увеличим число терминалов до 50, а число процессоров — до 10. Все остальные значения оставим прежними.

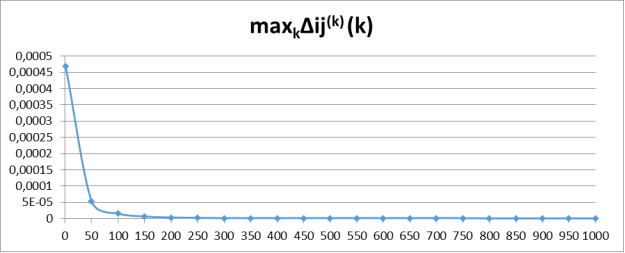
Рис. 6. График зависимости при N=50, M=10 и 1000 итерациях

При расширении системы график приближается к оси абсцисс ещё быстрее. Однако, значения выходных характеристик для 2-х методов на 1000-й итерации всё ещё различаются: для квазиэквивалентного метода N_ср = 34,292, M [t_р] = 21,83 и M_ср = 7,854, для точного метода — 34,302, 21,85, 7,85. Погрешности данных значений составляют 0,03 %, 0,09 % и 0,05 %соответственно. Если увеличить число итераций до 2000, значения выходных характеристик для обоих методов станут равными.

Сравним на трёх вышеописанных системах поведение выходных характеристик N_ср и M [t_р] при изменении входных параметров для квазиэквивалентного и точного методов. Для начала зафиксируем значения T_восст = 10, T_обд = 10, T_реш = 5 и исследуем зависимость N_ср(α), где α=1/T_отк (рис. 7). Количество итераций возьмём равным 2000.

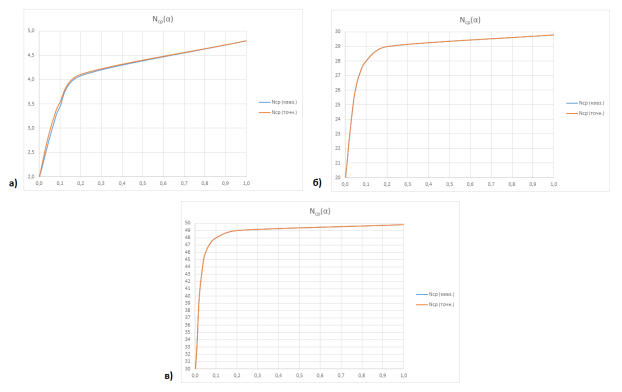
Рис. 7. Графики зависимости N_ср(α): а) для N=5, M=2; б) для N=30, M=5; в) для N=50, M=10

Как видим, для систем большой размерности (рис 7б и 7в) графики для обоих методов совпадают. Максимальная погрешность для системы с 5-ю терминалами и 2-мя процессорами (рис 7а) составила не более 4,5 %.

Теперь зафиксируем T_отк = 100 и исследуем зависимость N_ср(β), где β=1/T_восст (рис. 8). Остальные параметры оставим прежними.

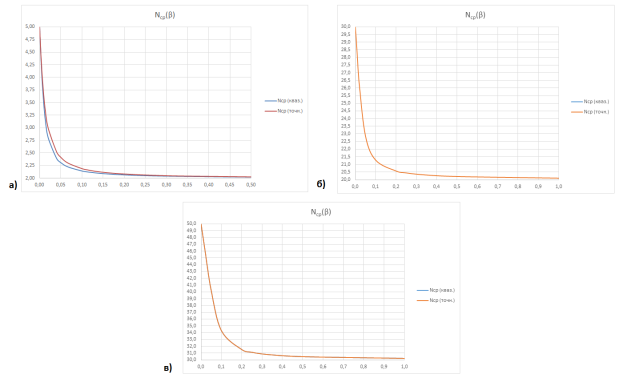
Рис. 8. Графики зависимости N_ср(β): а) для N=5, M=2; б) для N=30, M=5; в) для N=50, M=10

Равно как и в предыдущем случае, графики для систем большей размерности (рис. 8б и 8в) совпадают. Максимальная погрешность для системы с 5-ю терминалами и 2-мя процессорами (рис 8а) составила не более 6,4 %.

Исследуем зависимость M [t_р](λ), где λ=1/T_обд (рис. 9), с ранее зафиксированными значениями T_отк, T_восст и T_реш.

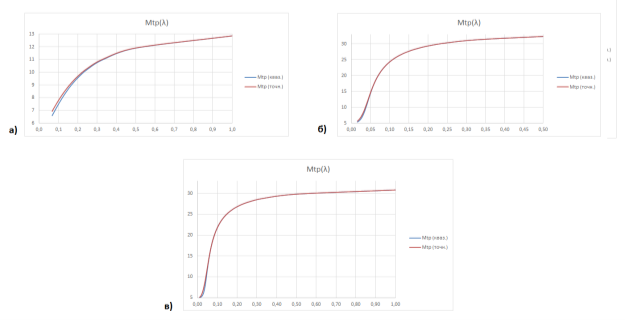
Рис. 9. Графики зависимостиM [t_р](λ): а) для N=5, M=2; б) для N=30, M=5; в) для N=50, M=10

Для 3-х рассмотренных систем графики сходятся по мере увеличения интенсивности обдумывания. Т. е. чем меньше T_обд, тем меньше выходная погрешность времени реакции. В среднем расхождение между значениями M [t_р](λ) для квазиэквивалентного и точного методов не превысило 3 %.

Рассмотрим финальную зависимость M [t_р](μ), где μ=1/T_реш (рис. 10).

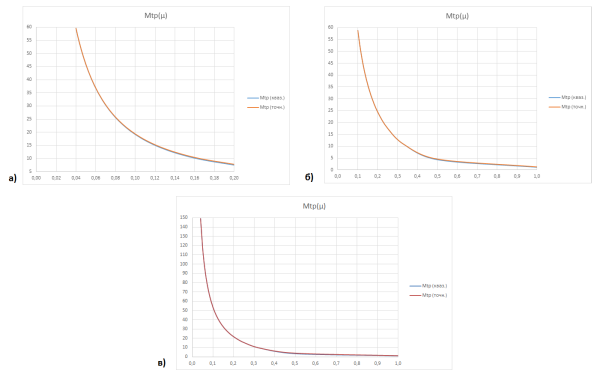
Рис. 10. Графики зависимости M [t_р](μ): а) для N=5, M=2; б) для N=30, M=5; в) для N=50, M=10

Ситуация прямо противоположная зависимости M [t_р](λ) — чем больше T_реш, тем меньше выходная погрешностьM [t_р]. Для исследованных систем расхождение между значениями M [t_р](μ) варьируется в пределах 1–2 %.

Из проведённых экспериментов можно сделать следующий вывод: по мере увеличения числа проводимых итераций уменьшается разность в значениях вероятностей состояний системы, а следовательно — и погрешность в значениях выходных параметров. И чем больше размерность рассматриваемой системы, тем меньше методическая погрешность метода квазиэквивалентного укрупнения. Иными словами, метод квазиэквивалентного укрупнения состояний вполне пригоден для анализа характеристик сложных систем.

Литература:

1. Шкатов П. Н. Стохастические модели в анализе информационно-вычислительных систем. Учебное пособие