1. Введение
Квантовые точки (КТ), полученные на основе различных гетероструктур, являются перспективными в применении различных оптоэлектронных приборах [1]. Теоретическое изучение спектра носителей в таких структурах является актуальным [2,3,6].
В работе [2] для КТ Si/SiO2 вмногозонном приближении эффективной массы для электронов и дырок численным методом решается уравнение Шредингера, а экситон моделировался с добавлением кулоновской энергии. В работе [3] для изучения КТ на основе InAs/GaAs рассматривают простую зону, а реальная структура зоны учитывается непараболичностью в модели Кейна.
В данной работе предлагается упрощённая модель КТ сферической формы. Для получения энергии экситона применен вариационный метод и приближение эффективной массы. Функционал энергии экситона получен в аналитическом виде. Учтены конечности высоты потенциальных барьеров для электрона и дырок, скачок их массы на границе гетероструктуры, а также непараболичность их зоны.
2. Модель
Рассмотрим сначала состояние одной частицы в КТ, гамильтониан которого в приближении эффективной массы имеет вид
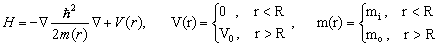 (1)
(1)
где, V0 –высота гетеробарьера, mi, mo –масса частиц внутри и вне КТ радиусом R. В границе гетероструктуры на волновую функцию
 (2)
(2)
налагается условия
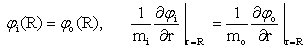 (3)
(3)
Для 1s –состояния получается хорошо известное уравнение
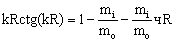 (4)
(4)
или
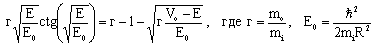 (5)
(5)
Экситонное состояние требует учёта притяжения электрона и дырок. Тогда имеет смысл искать полную волновую функцию системы вариационным методом. Попробуем заменить (2) упрощённой пробной функцией
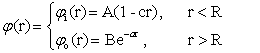 (6)
(6)
где, a и c вариационные параметры. Из граничных условий (3) найдем
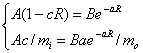 (7)
(7)
Исключив отсюда A и c имеем (далее можно положить B=1)
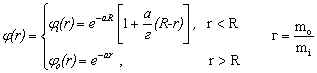 (8)
(8)
Усреднённая энергия 1s –состояния равна
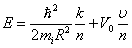 (9)
(9)
где, aR =a и
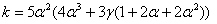 (10)
(10)
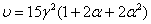 (11)
(11)
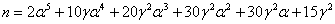 (12)
(12)
Приведем сравнение энергий (5) и (9) при следующих параметрах: V0 =1eV, mi=0.3me, mo=1me (см. Таблицу).
Таблица 1
|
R, Ангестрем |
10 |
20 |
30 |
40 |
50 |
60 |
|
E, eV из (5) |
0.422 |
0.169 |
0.091 |
0.057 |
0.039 |
0.028 |
|
E,eV из (9) |
0.426 |
0.171 |
0.092 |
0.057 |
0.039 |
0.028 |
Видно, что относительная ошибка составляет менее 1 % при R=10 ангстрем, и уменьшается с ростом радиуса КТ.
Гамильтониан экситона имеет вид (индекс 1 относится для электрона, 2 –для дырок)
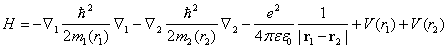 (13)
(13)
где
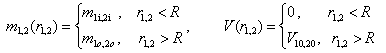 (14)
(14)
Диэлектрической проницаемости, считаем одинаковыми всюду.
Полную волновую функцию экситона запишем в виде 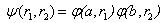 , где
, где 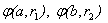 относится электрону и дырок соответственно, и имеет аналогично (8) вид
относится электрону и дырок соответственно, и имеет аналогично (8) вид
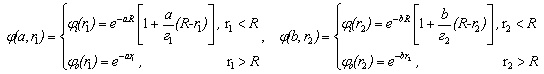 (15)
(15)
Здесь, 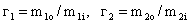 . Усредненная энергия экситона равна
. Усредненная энергия экситона равна
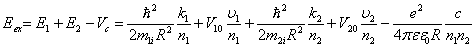 (16)
(16)
где, введены обозначения aR =a, bR =b и
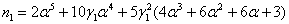 ,
, 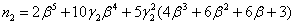
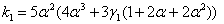 ,
, 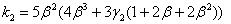
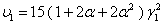 ,
, 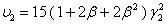 ,
, 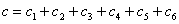 ,
,
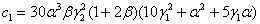 ,
, 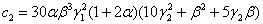
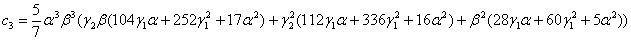
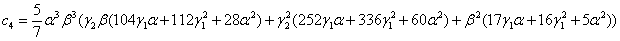
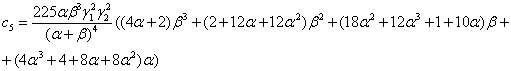
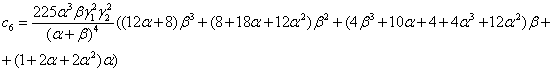
3. Обсуждение результатов
Используя модель КТ с барьером конечной высоты, Носака вычислял энергию экситонных состояний для CdS и получил сравнимые результаты с полученными другими авторами в приближении сильной связи [4]. Приведём сравнение его результатов с нашими вариационными значениями, полученными минимизацией (16) по a и b (см. Таблицу). Параметры расчета следующие: m1i =0.19 me, m2i=0.80me, 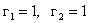 , e = 5.6, Ve=Vh=3.6 eV
, e = 5.6, Ve=Vh=3.6 eV
Таблица 2
|
R, Ангестрем |
10 |
20 |
|
Eex, eV, Nosaka [4] |
1.20 |
0.40 |
|
Eex, eV, (16) |
1.27 |
0.29 |
Видно, что наши результаты не хуже при R=10 ангстрем, и становится лучше с ростом радиуса КТ.
Параметры материалов КТ Si/SiO2 приведены в [2,6], и сравнены с несколькими экспериментальными данными. Поскольку наша модель является однозонным с изотропной массой, мы будем учитывать непараболичность зоны проводимости простой эмпирической формулой [5]
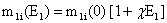 (17)
(17)
Здесь, c»2 eV-1, E1 –собственная энергия электрона в сферической яме, см.(16).
Использовали усреднённые по направлениям эффективные массы для электрона и дырок [6]: m1i=0.258 me, m1o =1me, m2i=0.21me, m2o=5me, и следующие параметры для материалов КТ: e=10, V10=3.2 eV, V20=4.3 eV. При прямой минимизации (16) для каждой пары значений a,b определяли E1 иm1i(E1) самосогласованно, т. е. итерационно с начальным значением m1i(0)=0.258me. Результаты расчетов при сравнении с экспериментальными данными приведены на рисунке.
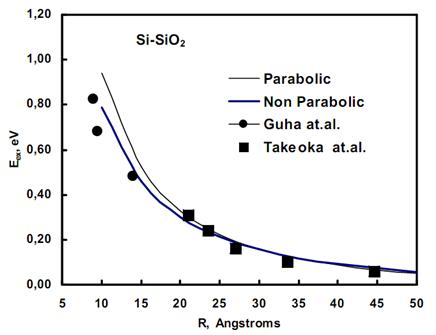
Рис. 1. Сравнение расчета с экспериментом
Вообще, при наличии кулоновского притяжения, одночастичные уровни сдвигаются. Однако, для КТ Si/SiO2 это сдвиг мало [2,6]. Наши тести показали, что, учет этого сдвига существенно не меняет полученных здесь результатов.
4. Заключение
Приведенная в настоящей работе вариационная схема расчета является достаточно простой, в конечном этапе получен алгебраический функционал для одночастичной и экситонной энергий. Показано, что структура сложной зоны может быть учтена с помощью модели Кейна. В присутствии внешних полей вариационная волновая функция для электрона и дырок могут деформироваться, что частично учитывается вариационными параметрами при минимизации полной энергии.
Если материал КТ и окружающая среда имеют различные диэлектрические проницаемости, необходимо учитывать силы электростатических изображений [2], которые в данной работе не учтены. А также предложенная схема расчета ограничена только основным состояниям экситона.
Литература:
1. L. Pavesi, L. Dal Negro, C. Mazzoleni, G. Franzo, and F. Priolo, Nature (London) 440,408 (2000).
2. A. S. Moskalenko, J. Berakdar, A. A. Prokofiev and I. N. Yassievich. Phys. Rev. B 76, 085427 (2007).
3. I. Filikhin, V. M. Suslov, M. Wu and B. Vlahovic, Physica E 41, 1358, (2009).
4. Y.Nosaka, J. Phys. Chem. 95, 5054–5058 (1991)
5. D. M. Riffe, J. Opt. Soc. Am.B, Vol.19, No.5, 1092–1100, (2002)
6. В. А. Бурдов. ФТП 36, 1233–1236, (2002)
7. S. Guha, B. Qadri, R. G. Musket, M. A. Wall, and T. Shimizu-Iwayama, J. Appl. Phys. 88, 3954 (2000).
8. S. Takeoka, M. Fujii, and S. Hayashi, Phys. Rev. B 62, 16820 (2000).







