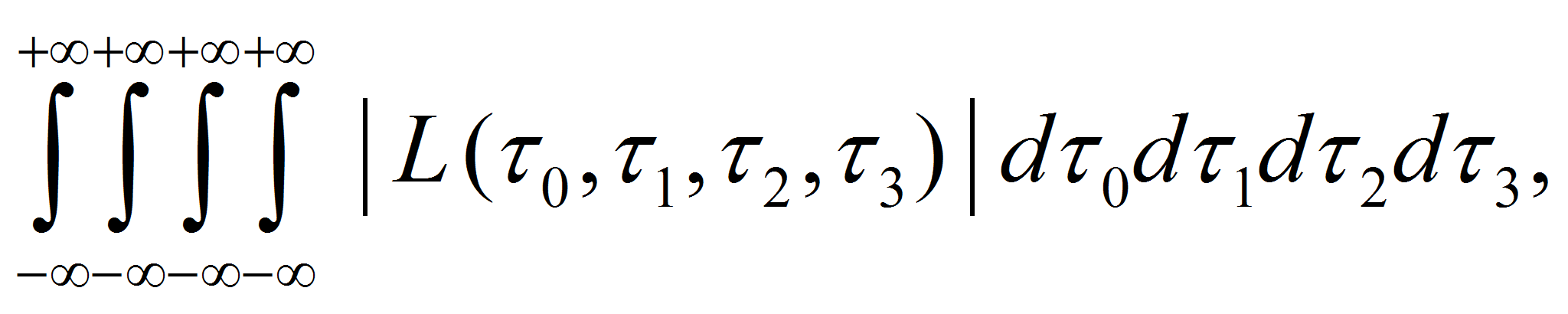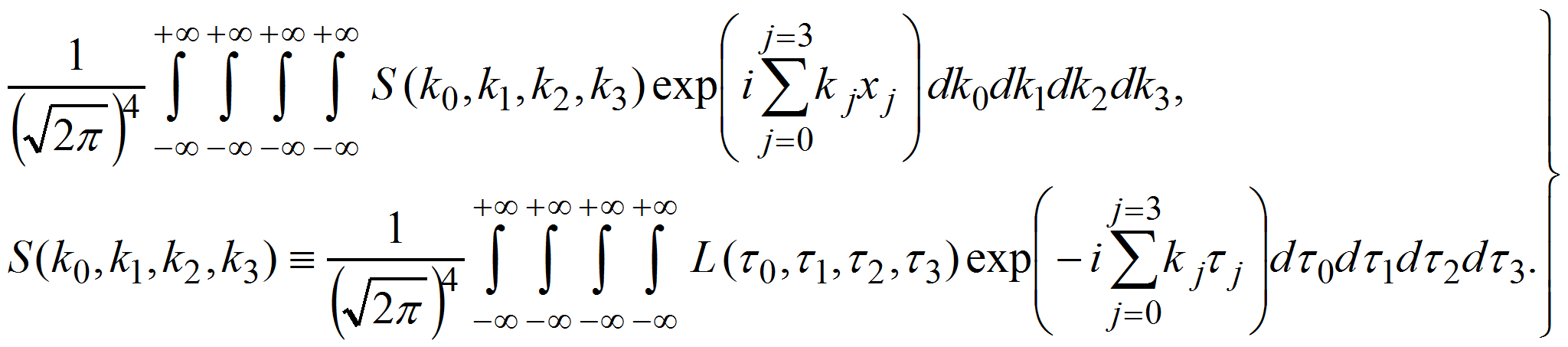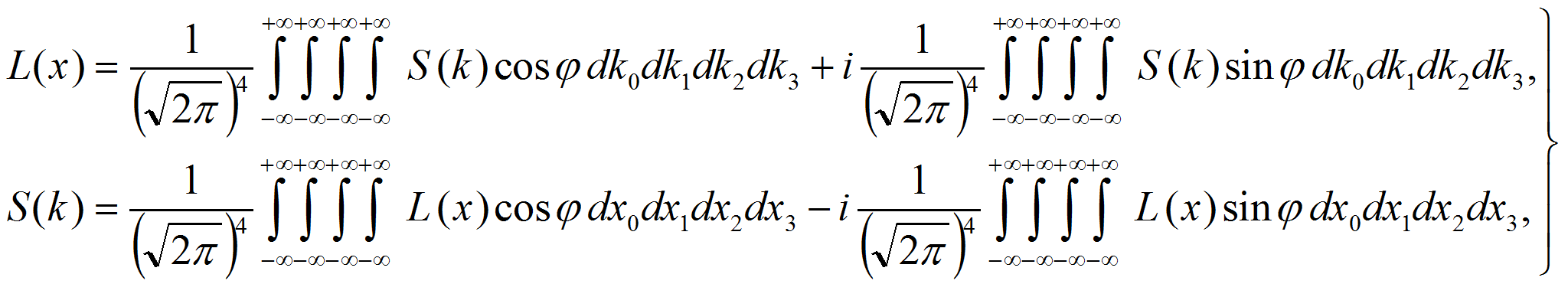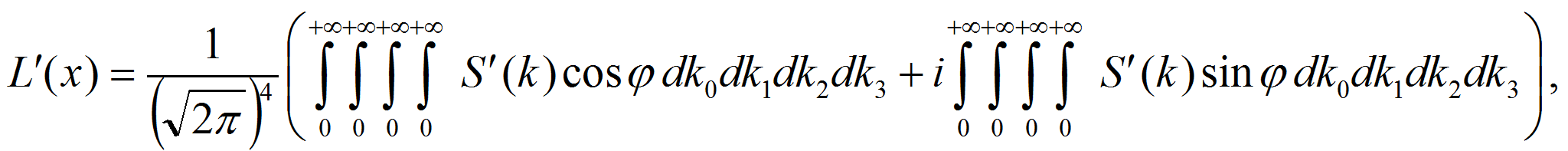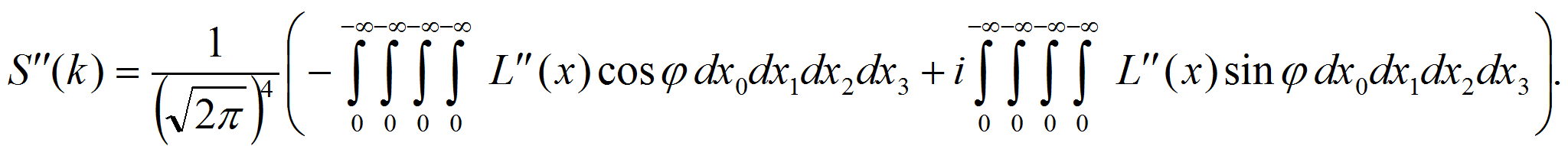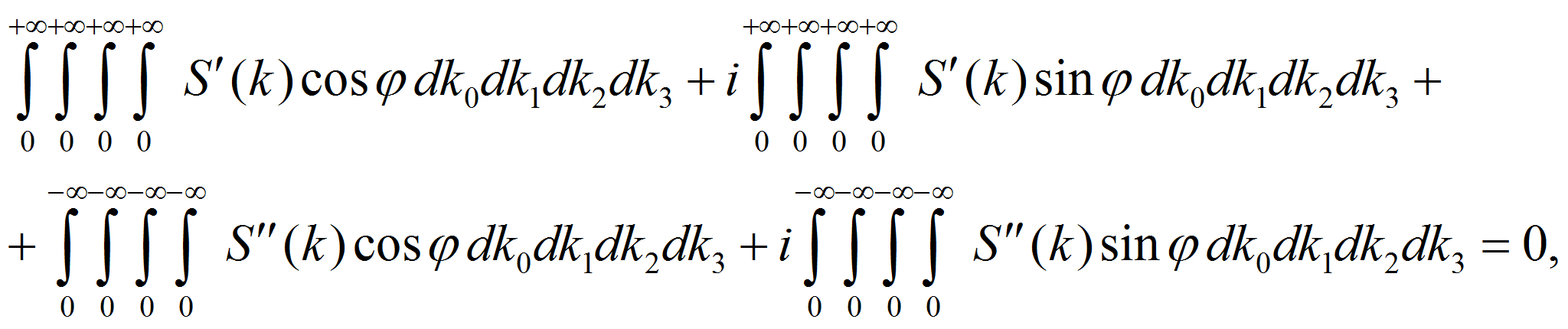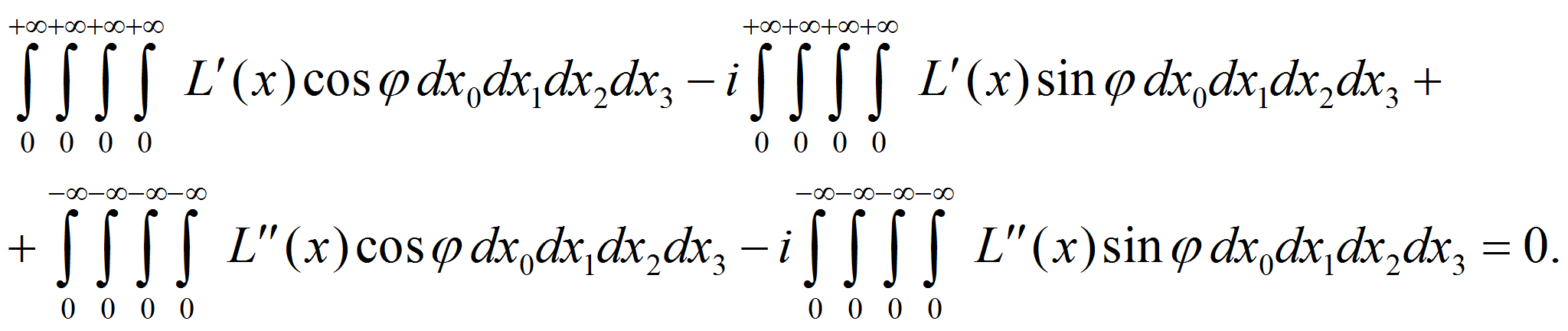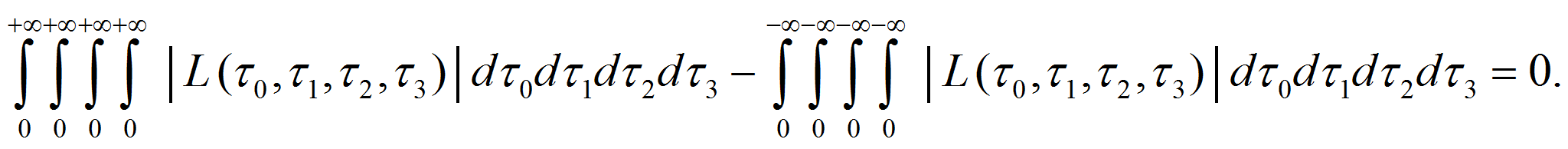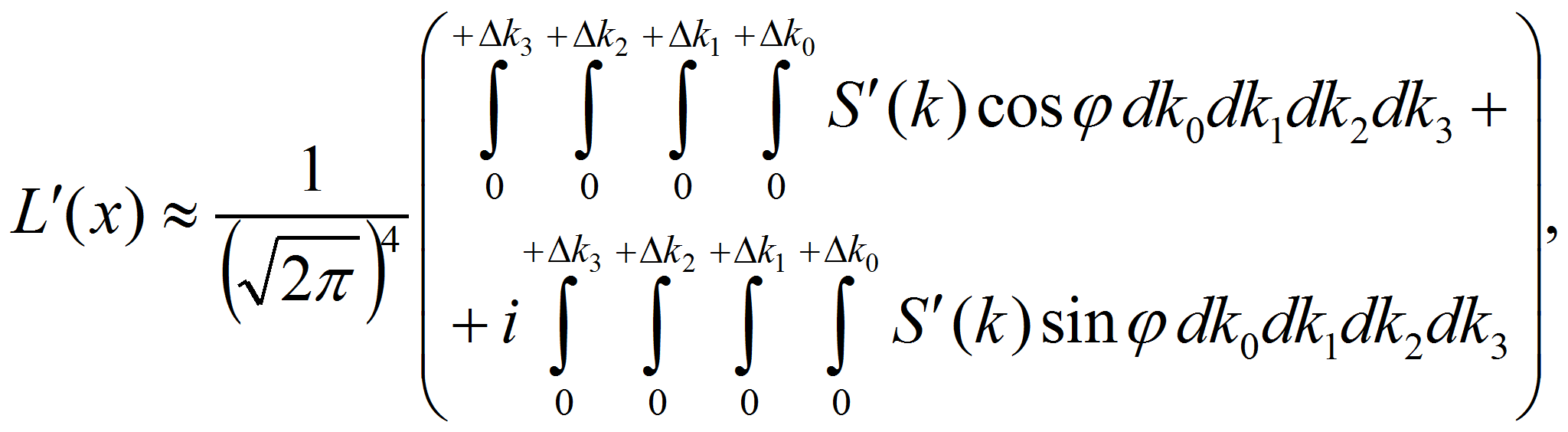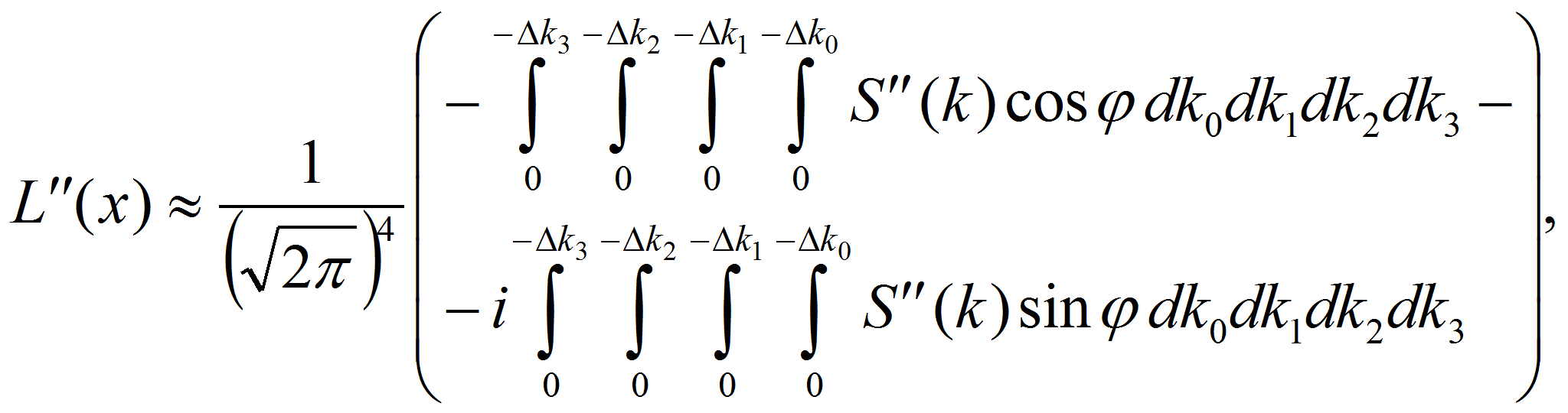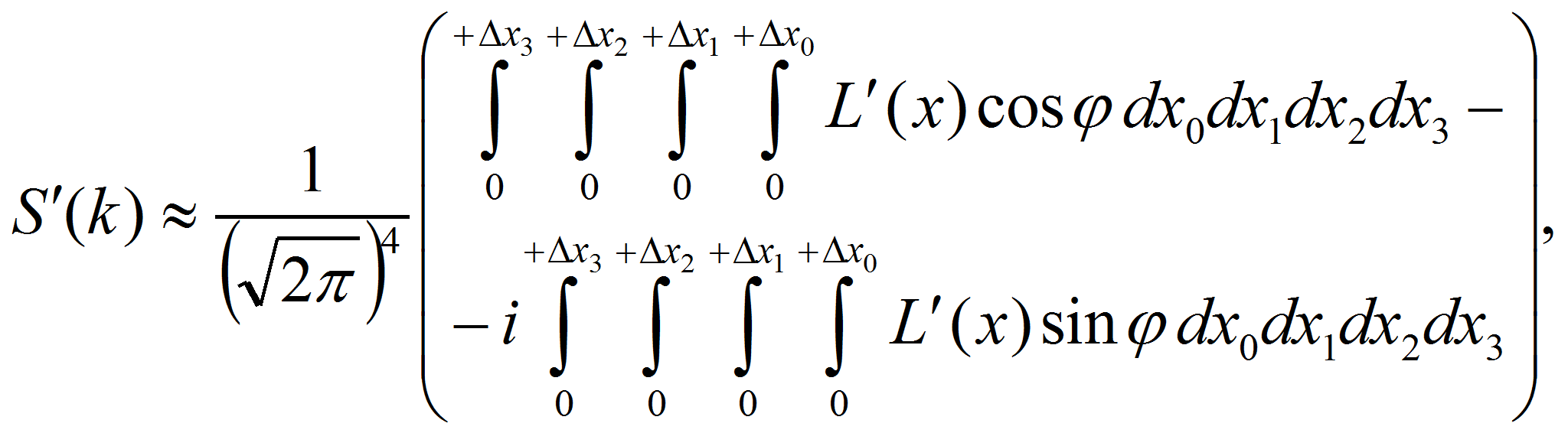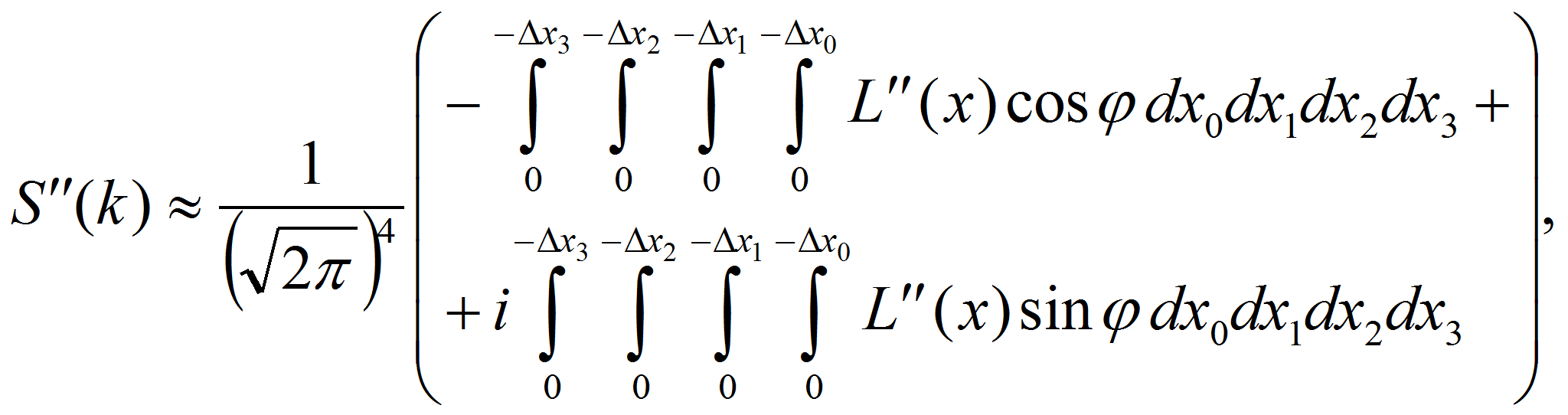По современным представлениям нейтрон не является бесструктурной частицей. Современное представление о структуре нейтрона основано на экспериментальных данных и квантовой хромодинамике. Считается надёжно установленным, что нейтрон является связанным состоянием трёх кварков. Время жизни нейтрона в свободном состоянии около 15 минут. Распад нейтрона, разрешённый законами сохранения энергии, электрического заряда, барионного и лептонного квантовых чисел, происходит в виде так называемого бета-распада: на протон, электрон и электронное антинейтрино. Однако в настоящее время, судя по научным публикациям, не существует математической модели, позволяющей рассчитать и, в результате расчёта, наблюдать физический процесс распада нейтрона.
В данной статье рассмотрен оригинальный подход к компьютерному моделированию процесса бета-распада нейтрона на основе кратного интеграла Фурье.
Представим себе, что нейтрон занимает некоторый
пространственно-временной объём. Тогда каждой
пространственно-временной точке структуры нейтрона можно поставить в
соответствие некоторое значение плотности функции Лагранжа:
![]() ,
,
![]() – пространственно-временные координаты (
– пространственно-временные координаты (![]()
временная координата,
временная координата,
![]()
пространственные координаты). Тогда кратный интеграл Фурье,
порождённый функцией
пространственные координаты). Тогда кратный интеграл Фурье,
порождённый функцией
![]() для которой существует интеграл
для которой существует интеграл
по определению есть
Функцию
![]() логично интерпретировать как спектр плотности функции Лагранжа, а
координаты
логично интерпретировать как спектр плотности функции Лагранжа, а
координаты
![]()
как компоненты волнового 4-вектора (будет показано, что
как компоненты волнового 4-вектора (будет показано, что
![]() следует рассматривать как физически наблюдаемую величину).
Совокупность функций вида
следует рассматривать как физически наблюдаемую величину).
Совокупность функций вида
в современной теории информации принято называть парой.
Невозможно допустить, что пространство-время во
внутренней структуре нейтрона является плоским. В общем случае
пространственно-временную метрику можно задать, фундаментальным
метрическим тензором
![]() причём
причём
![]() Тогда фаза в экспоненциальных функциях в (3) будет равна
Тогда фаза в экспоненциальных функциях в (3) будет равна
Здесь и далее
![]()
![]()
ковариантные компоненты и координаты, соответственно.
ковариантные компоненты и координаты, соответственно.
Пользуясь формулами Эйлера, экспоненциальные функции в (3) можно представить в виде действительных и мнимых слагаемых:
Тогда из (3) и (5) следует
Кроме того, функции (6) можно разложить на составляющие, в которых нижние пределы интегрирования будут равны нулю:
Согласно предложенному подходу и CPT-теореме, барионной симметрии во всей бесконечной Вселенной должна соответствовать следующая нормировка:
то есть
Нормировка (13) означает, что (с точки зрения данного подхода) количество вещества и количество антивещества во всей бесконечной Вселенной строго одинаковы, то есть интеграл (1) можно представить в виде (16), причём этот интеграл равен нулю:
Это значит, что интеграл в (16) с положительными значениями пространственно-временных кординат в верхних пределах интегрирования нужно отнести к веществу, а интеграл с отрицательными значениями пространственно-временных кординат к антивеществу. То же самое можно сказать о (14) и (15).
Таким способом, то есть путём введения нормировки (13), может быть решена одна из актуальных проблем космологии: проблема барионной асимметрии.
Верхние пределы интегрирования в (1) и в (9)÷(12)
бесконечности по всем компонентам
![]() и координатам
и координатам
![]() .
Это значит, что для применения интегралов (9)÷(12) к
решению поставленной задачи требуются какие-то дополнительные
условия, исключающие указанные бесконечности. Иначе возникает
противоречие.
.
Это значит, что для применения интегралов (9)÷(12) к
решению поставленной задачи требуются какие-то дополнительные
условия, исключающие указанные бесконечности. Иначе возникает
противоречие.
Действительно, согласно исходному представлению, каждой пространственно-временной точке структуры нейтрона соответствует определённая плотность функции Лагранжа. Но чтобы её точно определить по (7) совместно с (9) и (10), нужно в (9) и (10) точно задать спектр плотности функции Лагранжа.
В свою очередь, спектр плотности функции Лагранжа
определяется точно
через плотность функции Лагранжа с помощью (8) вместе с (11) и (12) с
пределами интегрирования от нуля до
![]() в (11) и от нуля до
в (11) и от нуля до
![]() в (12).
в (12).
Таким образом, чтобы точно
определить плотность функции Лагранжа в
какой-либо пространственно-временной точке, принадлежащей структуре
нейтрона, необходимо каким-то способом сосредоточить в этой точке
полную информацию о пространственно-временном распределении плотности
функции Лагранжа не только в наблюдаемой Вселенной, но и за её
пределами: от
![]() до
до
![]()
по всем четырём координатам
по всем четырём координатам
![]() .
И это относится к каждой пространственно-временной точке нейтрона. В
таком представлении вся структура нейтрона должна быть заполнена
бесконечным объёмом информации о распределении плотности функции
Лагранжа и её спектра по всей Вселенной.
.
И это относится к каждой пространственно-временной точке нейтрона. В
таком представлении вся структура нейтрона должна быть заполнена
бесконечным объёмом информации о распределении плотности функции
Лагранжа и её спектра по всей Вселенной.
Можно ли принять такую точку зрения? Если "нет", то, как следствие, плотность функции Лагранжа и её спектр принципиально не могут быть точно определены ни в одной пространственно-временной точке структуры нейтрона. А если "да", то структура нейтрона каким-то образом оказывается переполненной, причём в динамике, бесконечным объёмом информации.
Естественный и, похоже, единственный выход в такой ситуации это ограничить в (9)÷(12) верхние пределы интегрирования. Природа, по-видимому, так и поступает, "осуществляя" расчёт структуры всех материальных частиц и физических полей приближённо:
![]()
![]() – квадратичные отклонения (от нуля) компонент
волнового 4-вектора и квадратичные отклонения (от нуля)
пространственно-временных координат, соответственно.
– квадратичные отклонения (от нуля) компонент
волнового 4-вектора и квадратичные отклонения (от нуля)
пространственно-временных координат, соответственно.
Между квадратичными отклонениями существует связь:
В квантовой теории подобные соотношения (соотношения неопределённостей Гейзенберга между проекциями импульса и пространственными координатами, энергией и временем) играют важнейшую роль и органически связаны с принципом дополнительности Н. Бора.
Значение соотношений (21) трудно переоценить. Можно сказать, что на этих соотношениях основан весь излагаемый здесь подход. Они имеют следующую интерпретацию. Вблизи некоторой пространственно-временной точки волны спектра плотности функции Лагранжа могут иметь примерно одну и ту же фазу, и в результате все амплитуды волн сложатся, а в вдали от этой точки будут гасить друг друга из-за разнобоя в фазах. Таким образом, ненулевая плотность функции Лагранжа будет сосредоточена вблизи этой пространственно-временной точки. Понятие "вблизи" определяется соотношением длины волны и пространственного расстояния до этой точки. Если расстояние соизмеримо с длиной волны, то применимо понятие "вблизи", если нет, то волны будут взаимно гасить друг друга, и плотность функции Лагранжа, а также её спектр устремяться к нулю. Оказывается, размер пространственно-временной области, в которой волны могут иметь примерно одинаковую фазу, обратно пропорционален ширине спектра в этой области.
Таким образом, нет смысла производить интегрирование за
пределами некоторых значений
![]() и
и
![]() .
.
В каждом конкретном случае принятые значения квадратичных отклонений, естественно, нужно обосновывать. Например, при моделировании нейтрона квадратичные отклонения пространственных координат не должны быть меньше его физически наблюдаемых размеров, а при моделировании распада нейтрона и процесса образования атома водорода не менее физически наблюдаемых размеров атома водорода.
И ещё. Если совокупность функций
![]() и
и
![]() с некоторыми значениями квадратичных отклонений в качестве пределов
интегрирования принимается, согласно (13), в качестве математического
описания структуры, например, нейтрона, то совокупность функций
с некоторыми значениями квадратичных отклонений в качестве пределов
интегрирования принимается, согласно (13), в качестве математического
описания структуры, например, нейтрона, то совокупность функций
![]() и
и
![]() будет являться математическим описанием структуры антинейтрона. Таким
образом, инверсия по компонентам
будет являться математическим описанием структуры антинейтрона. Таким
образом, инверсия по компонентам
![]() и координатам
и координатам
![]() приводит в рамках данного подхода к замене частиц античастицами.
приводит в рамках данного подхода к замене частиц античастицами.
Модельный эксперимент может быть осуществлён с помощью (17)÷(20) и (21) с определёнными пределами интегрирования в (21).
Если в структуре нейтрона ограничиться только физически
наблюдаемой областью сильных взаимодействий, то пределы
интегрирования можно задать следующим способом. Энергия покоя
нейтрона определяется как
![]() (
(![]()
масса покоя нейтрона,
масса покоя нейтрона,
![]()
скорость света в вакууме). Этой энергии соответствует энергия кванта
скорость света в вакууме). Этой энергии соответствует энергия кванта
![]() (
(![]()
постоянная Планка,
постоянная Планка,
![]()
частота кванта). Отсюда, в частности, следует, что
частота кванта). Отсюда, в частности, следует, что
![]() с-1
это так называемое характерное число (по порядку величины) в физике
элементарных частиц.
с-1
это так называемое характерное число (по порядку величины) в физике
элементарных частиц.
Отношение
![]() имеет размерность длины. Это отношение равно примерно
имеет размерность длины. Это отношение равно примерно
![]() м
и по порядку величины соответствует радиусу нейтрона. Поэтому
величину
м
и по порядку величины соответствует радиусу нейтрона. Поэтому
величину
можно рассматривать как квадратичные отклонения координат для нейтрона.
Величину
обратную квадратичному отклонению координат, имеет смысл принять в качестве квадратичного отклонения компонент волнового 4-вектора.
Подобные рассуждения можно применить также и к
наблюдаемой Вселенной. Отношение
![]() (
(![]()
постоянная Хаббла) принято считать её радиусом (это расстояние до
горизонта событий). Он равен примерно
постоянная Хаббла) принято считать её радиусом (это расстояние до
горизонта событий). Он равен примерно
![]() м.
Поэтому величину
м.
Поэтому величину
можно принять по аналогии с нейтроном как квадратичное отклонение координат в крупномасштабной структуре нашей Вселенной.
Квадратичные отклонения компонент волнового вектора крупномасштабной структуры Вселенной можно задать в виде обратного отношения
которое имеет размерность, обратную размерности длины.
Заметим, кстати, что
известное (по порядку величины) число.
Можно показать, что при моделировании по (17)÷(20) в сочетании с (21) возникновение структуры нейтрона происходит автоматически, без какого-либо внешнего вмешательства. По сути в данной статье предложено компьютерное моделирование функциональной схемы, изображённой на рис. 1.
Рис. 1. Функциональная схема компьютерной реализации математической модели по (6)
На рис. 2 представлен однолинейный аналог подобной схемы.
Рис. 2. Функциональная схема генератора на двух интеграторах
С помощью второй схемы можно показать,
что в схеме, изображённой на рис. 1, присутствует положительная
обратная связь (по терминологии теории автоматического управления),
которая обеспечивает без внешнего вмешательства возникновение
ненулевых значений функций
![]() и
и
![]() .
Другими словами, состояние процессов при нулевых значениях
.
Другими словами, состояние процессов при нулевых значениях
![]() и
и
![]() является неустойчивым, то есть в системе возникают автоколебания за
счет действия положительной обратной связи.
является неустойчивым, то есть в системе возникают автоколебания за
счет действия положительной обратной связи.
Действие положительной обратной связи можно показать на простом примере однолинейной схемы (генератора), изображённой на рис. 2. Причём положительная обратная связь обусловлена инвертором, который присутствует в структуре генератора.
Пользуясь преобразованием Лапласа, запишем для схемы, изображённой на рис. 2, две передаточные функции:
![]() изображения функций
изображения функций
![]() ;
;
![]()
постоянные времени интеграторов,
постоянные времени интеграторов,
![]()
комплексная переменная.
комплексная переменная.
Перемножим (27) и (28). В результате получим следующее равенство:
откуда
Умножим (30), например, на
![]() .
Результатом будет изображение по Лапласу
.
Результатом будет изображение по Лапласу
дифференциального уравнения 2-го порядка.
Оригинал изображения (31) имеет следующий вид:
Решением уравнения (32) является периодическая функция времени
![]() ,
,
![]() и
и

амплитуда, фаза и круговая частота, соответственно.
амплитуда, фаза и круговая частота, соответственно.
Принципиально то же самое происходит и в схеме, изображённой на рис. 1. В этой схеме положительная обратная связь обусловлена знаками "минус" в системе (17)÷(20). Знаки "минус" выполняют такую же функцию, что и инвертирование в схеме, изображённой на рис. 2, то есть приводят к самовозбуждению. Но поскольку интеграторы на рис. 1 имеют структуру (17)÷(20), то результатом расчета, судя по всему, будет процесс возникновения и распада нейтрон-антинейтронной пары частиц.
Выводы.
Основной вывод состоит в том, что в данном подходе все реально существующие частицы, античастицы, кванты это физически наблюдаемые компактифицированные спектры плотности функции Лагранжа.
Рождение и структуру нейтрона можно наблюдать путём компьютерного моделирования по (17)÷(20), (21). При моделировании этого процесса значения квадратичных отклонений компонент волнового 4-вектора и пространственно-временных координат в (21) первоначально нужно принять по (22), (23). Начальные условия, как было показано, могут быть нулевыми.
Бета-распад нейтрона можно наблюдать тоже путём компьютерного моделирования по (17)÷(20). Но при моделировании этого процесса значения квадратичных отклонений пространственно-временных координат нужно принять не менее размера атома водорода, а значения квадратичных отклонений компонент волнового 4-вектора должны быть по-возможности больше, так как процесс распада нейтрона связан с рождением высокочастотного электронного антинейтрино.
Согласно закону сохранения барионного заряда вместе с возникновением нейтрона в результате расчёта одновременно должен возникнуть антинейтрон. Структура функций (17)÷(20), рассматриваемая совместно с (21), и теорема CPT-симметрии указывают на то, что возникновение пары нейтрон-антинейтрон с последующим её распадом является неизбежностью. Следовательно, в модельном эксперименте при соответствующем выборе квадратичных отклонений возможно наблюдение возникновения и распада нейтрон-антинейтронной пары.
Согласно предложенному подходу, в процессе расчёта по (17)÷(20), (24), (25), в принципе, возможно наблюдение возникновения и эволюции нашей Вселенной, а при расчёте по (7)÷(12), то есть при бесконечных верхних пределах интегрирования по всем компонентам и координатам, в принципе, можно было бы наблюдать структуру и динамику эволюции всей бесконечной Вселенной. Но, наверно, можно доказать, что для решения таких задач компьютер с требуемой производительностью создать невозможно. Впрочем для расчёта процесса возникновения нейтрон-антинейтронных пар и начала процесса их распада производительности современных (или будущих) суперкомпьютеров, возможно, будет достаточно.
Раработка программы для ЭВМ по (17)÷(20), (21), (24), (25) и соответствующие модельные эксперименты могли бы, по-видимому, решить проблему сингулярного состояния нашей Вселенной важнейшую проблему современной космологии.