В работе формализованы и исследованы две модели многоагентного управления в коррупционных сетях социума. Предложены алгоритмы нахождения равновесия Курно-Нэша и компромиссного решения в этих моделях. Решены два численных примера.
Ключевые слова:социум, коррупция,конкуренция, математическое моделирование.
На текущее состояние и эволюционное развитие общества влияют множество факторов: бедность, социальное неравенство, преступность, коррупция и др. В обществе обсуждаются как древние проблемы, так и вновь возникающие, делаются многочисленные прогнозы [7–9, 12, 23–25, 28,]. Однако, как правило, на приводится строгих подтверждений проблем на основе статистического материала с учетом эволюционного развития общества. Не достаточно и обоснованных математических моделей, позволяющих описать взаимодействие социальных групп [14, 15 и] дать как количественный, так и качественные прогноз возможного состояния общества в будущем [26, 27, 38], выявить бифуркационные направления развития. Одним из направлений, по которому пошел процесс преобразований в России, начатый в 1990-е годы, — «сырьевая» экономика с коррупционной составляющей в управлении. Ниже предлагаются модели описания коррупционных процессов на основе организационной структуры рыночной экономикой [3– 6, 10, 16, 23, 29–33] и основанные на принципах математической популяционной биологии.
Модель 1. Формализуется коррупционная сеть в рамках некоторого социума. Эта коррупционная сеть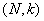 
состоит из вершин, соответствующих коррумпированным посредникам, предлагающих услуги посредничества, составляющих множество 
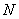и ребер, соединяющих их. На множестве ребер задана функция посреднических издержек 
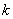, сопоставляющая каждому ребру, соединяющему вершины 
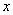и 
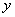, неотрицательное число 
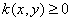, представляющее собой издержки по установлению контакта между посредником и агентом, которым может оказаться последний агент коррупционной цепочки, продающий коррупционные услуги. В узлах сети, составляющих множество 
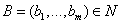, располагаются потребители коррупционных услуг, производимых коррупционерами, которые для приобретения этой коррупционной услуги обращаются к посредникам, составляющим множество
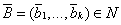, задача которых — осуществлять посреднические услуги для потребителей коррупционных услуг. Требуется в некоторых узлах сети расположить коррупционеров, составляющих множество 
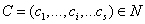, которые осуществляют формирование и продажу коррупционных услуг. Для производства коррупционных услуг коррупционеры используют ресурсы (деньги), составляющие множество 
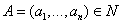, с помощью которых они формируют коррупционные услуги. Коррупционеры желают разместиться в узлах сети наиболее выгодным для них образом с точки зрения максимизации получаемого дохода от продажи и производства этих коррупционных услуг. Определена функция, описывающая объем 
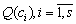коррупционных услуг, который получается при использовании капитала коррупционеров 
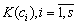, и их профессиональных навыков 
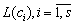, уровень которых повышается за счет ресурсов обучения. Коррупционеры стремятся максимизировать их прибыль, принимая в расчет число потребителей 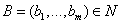коррупционных услуг, приезжающих к ним за покупкой произведенной услуги 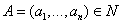, и объемы совершаемых покупок 
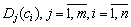, которые предполагаются заданными для каждого потребителя коррупционных услуг. Предполагается, что потребитель направляется к тому коррупционеру для приобретения произведенной коррупционной услуги, где его суммарные затраты 
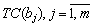, с учетом посреднических издержек минимальны. Доход каждого коррупционера складывается из суммы денег, полученных им от потребителей коррупционных услуг и определяется формулой 
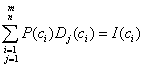, где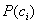 
— цена на коррупционную услугу в 
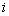- м магазине, 
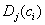— спрос 
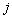- ого потребителя на товар 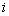-ого коррупционера, 
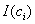- доход 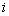-ого коррупционера. Коррупционеры договариваются между собой об их размещении в вершинах сети на основе какого-либо теоретико-игрового принципа оптимальности, скажем, компромиссного решения или равновесия Курно-Нэша.
Модель 2. Коррупция — общий термин, обозначающий использование своего положения в обществе в корыстных целях. В рассматриваемой модели 2 изучается случай, когда за предоставляемую услугу коррупционер получает взятку. Лицо, принимающее взятку, является агентом типа (которых можно называть чиновниками или федеральными служащими), составляющих множество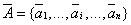 
, а лицо, вручающее взятку, является агентом типа 
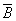(которых можно называть клиентами или обычными служащими), составляющих множество 
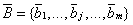. Имеется коррупционная сеть 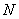, с каждым промежуточным узлом которой ассоциируются потенциальные коррупционеры-посредники, составляющие множество 
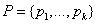, которые за свои посреднические услуги (оказание услуг в организации контакта в коррупционной цепочке) взимают противоправное средство (взятка, подкуп), составляющих множество 
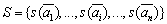. Чиновник 
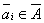, обладает потенциальными возможностями выполнить какую-либо функцию при условии получения взятки. Вручитель взятки, агент множества , может осуществить её передачу только лишь через посредников из множества 
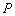, расположенных в данной коррупционной сети 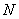. Передача контакта от одного посредника к другому сопровождается выплатой промежуточной взятки посреднику 
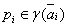, где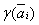 
множество смежных узлов сети. При прохождении всей коррупционной цепочки клиент получает услугу, сопровождающуюся получением дохода, зависящим от размера взятки. Коррупционер 
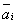из множества 
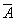выплачивает агенту 
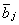из множества 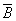какой-либо противоправный доход. В рамках коррупционной сети у каждого агента есть задача получения противоправного дохода. Каждый взяткополучатель имеет свои расценки, и хочет максимизировать свой доход, а каждый клиент стремится получить максимальную прибыль при минимальных издержках. Нужно найти кратчайший путь агентов из множества 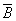для передачи взятки агенту из множества . Есть ограничение: функция стоимости услуг коррупционного посредника, которая представляет собой определенную денежную величину 
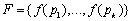, больше размера которой посредник не может получить.
Модель 3. Для моделирования коррупционных процессов можно использовать и методы математической популяционной биологии [1, 37]. При таком подходе сообщество взаимодействующих субъектов в экономической среде разбивается на группы, взаимодействующие между собой [18, 34]. При этом группа коррупционеров может рассматриваться как популяция паразитов или популяция хищников. В роли трофического ресурса или «хозяина» могут выступать материальные ресурсы. В модели могут быть учтены властная структура и структура, ограничивающая коррупцию [35, 36]. Формирование системы показателей, на основании анализа которых разрабатывается модель, представляет собой достаточно сложную, но решаемую задачу [13].
Поскольку взаимодействующие субъекты располагаются на территории, то и «свойства» коррупции в разных регионах разные [35]. Здесь можно использовать либо разбиение территории на несколько регионов [34], либо строить модель для системы с распределенными параметрами [17]. Изменение основных показателей, пусть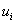 
(
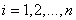), в системе происходит «случайным» образом и кинетика их роста, как и в случае биологических популяций в линейном приближении подчиняется экспоненциальной зависимости [22, 24, 26–28].
Для описания изменения показателей можно использовать систему дифференциальных уравнений
,
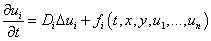
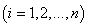где 
— оператор Лапласа,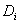 
— параметры, характеризующие диффузионные процессы, 
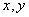— пространственные координаты, 
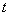— время, 
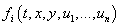— «кинетические» функции, описывающие взаимодействие социальных групп между собой
Для описания развития изолированной группы на территории можно использовать модели одиночной популяции [2, 20]. Коррупция возникает в центре сообщества и распространяется на периферию. Эволюционные уравнения имеют решения в виде автоволн [19], позволяющие моделировать распространение коррупционных процессов на территории. Коррупцию в системах с распределенными параметрами можно рассматривать и как злокачественную опухоль, уничтожающую материальные ресурсы [11]. Модели социальных процессов достаточно сложны, представляют собой нелинейные системы уравнений, решения которых строится с применением численных методов [21].
Литература:
1. Базыкин А. Д. Нелинейная динамика взаимодействующих популяций. Москва-Ижевск: Институт компьютерных технологий. — 2003. 368 с.
2. Горбунова Е. А., Колпак Е. П. Математические модели одиночной популяции // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления.– 2012. — Вып. 4. — С. 18–30.
3. Гордеев Д. A., Малафеев О. А. Титова Н. Д. Стохастическая модель принятия решения о выводе на рынок инновационного продукта // Вестник гражданских инженеров — 2011 — № 2. — С. 161–166.
4. Гордеев Д. А., Малафеев О. А., Титова Н. Д. Probabilistic and Deterministic Model of the Influence Factors the Activities of the Organization to Innovate// Экономическое возрождение России — 2011 — № 1. — С.73–82.
5. Григорьева К. В., Малафеев О. А. Динамический процесс кооперативного взаимодействия в многокритериальной (многоагентной) задаче почтальона // Вестник гражданских инженеров — 2011 — № 1. — С. 150–156.
6. Григорьева К. В., Иванов А. С., Малафеев О. А. Статическая коалиционная модель инвестирования инновационных проектов // Экономическое возрождение России — 2011 — № 4. — С. 90–98.
7. Гринин Л. Е., Коротаев А. В. Макроэволюция и Мир-Система: новые грани концептуализации // История и современность. — 2008. — № 1. — С. 3–31.
8. Гринин Л. Е., Коротаев А. В.Революция VS демократия (революция и контрреволюция в Египте) // Полис (Политические исследования). — 2014. — № 3. — С. 139–158.
9. Гринин Л. Е., Коротаев А. В.Социальная макроэволюция и исторический процесс (к постановке проблемы) // Философия и общество. — 2007. — № 4 (48). — С. 17–50.
10. Дроздова И. В. Моделирование процессов реконструкции жилищно-коммунального хозяйства мегаполиса в условиях конкурентной среды: монография / И. В. Дроздова, О. А. Малафеев, Г. Д. Дроздов — М-во образования и науки Российской Федерации, Федеральное агентство по образованию, Санкт-Петербургский гос. ун-т сервиса и экономики — Санкт-Петербург, 2008.
11. Жукова И. В., Колпак Е. П. Математическая модель солидной опухоли // Естественные и математические науки в современном мире. — 2013. — № 13. — С. 18–25.
12. Исаев Л. М., Коротаев А. В Египетский переворот 2013 года: опыт эконометрического анализа // Азия и Африка сегодня. — 2014. — № 2 (679). — С. 14–20.
13. Карелин В. В Один подход к задаче оценки параметров динамической системы в условиях неопределенности // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2012. — № 4. — С. 31–36.
14. Колесин И. Д. Моделирование взаимодействия этнокультур // Известия Российской академии наук. Теория и системы управления. — 2005. — № 2. — С. 75–80.
15. Колесин И. Д. Принцип максимума в организаторской деятельности // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2008. — № 4. — С. 9–13.
16. Колокольцов В. Н., Малафеев О. А. Динамические конкурентные системы многоагентного взаимодействия и их асимптотическое поведение (часть I) // Вестник гражданских инженеров — 2010 — № 4 — С. 144–153.
17. Колпак Е. П. Введение в механику сплошных сред учебное пособие / Е. П. Колпак; С.-Петерб. гос. ун-т. СПб. 2004.
18. Колпак Е. П., Горбунова Е. А., Балыкина Ю. Е., Гасратова Н. А. Математическая модель одиночной популяции на билокальном ареале // Молодой ученый. — 2014. — № 1 (6). — С. 28–33.
19. Колпак Е. П., Горбунова Е. А., Жукова И. В. Математическая модель популяционной волны // Естественные и математические науки в современном мире. — 2014. — № 16. — С. 25–41.
20. Колпак Е. П., Горбунова Е. А., Столбовая М. В., Балыкина Ю. Е Математическая модель логистической популяции на линейном ареале // Молодой ученый. — 2014. — № 3 (62). — С. 6–14.
21. Колпак Е. П., Жукова И. В., Степанова Д. С., Крицкая А. В. О численных методах решения эволюционных уравнений на примере математической модели «хищник-жертва» // Молодой ученый. — 2014. — № 4 (63). — С. 20–30.
22. Колпак Е. П., Столбовая М. В. Математическая модель кинетики роста растений // Журнал научных публикаций аспирантов и докторантов. — 2013. — № 12 (90). — С. 230–232.
23. Короновский А. А., Стриханов М. Н., Трубецков А. И., Храмов А. Е. Анализ и прогноз тенденций изменения научно-педагогического потенциала профессорско-преподавательского состава высшей школы России // Науковедение. — 2002. — № 2. — С. 82.
24. Короновский А. А., Трубецков Д. И., Храмов А. Е Динамика численности населения как процесс, подчиняющийся уравнению диффузии // Доклады Академии наук. — 2000. — Т. 372. № 3. — С. 397.
25. Коротаев А. В., Зинькина Ю. В Египетская революция 2011 года: социодемографический анализ // Историческая психология и социология истории. — 2011. — Т. 4. — № 2. — С. 5–29.
26. Коротаев А. В., Зинькина Ю. В. Прогнозирование социополитических рисков: ловушка на выходе из мальтузианской ловушки // Информационный бюллетень ассоциации История и компьютер. — 2010. — № 36. — С. 101–102.
27. Коротаев А. В., Зинькина Ю. В. Социально-экономическое развитие и прогноз структурно-демографических рисков стран Восточной Африки (Кения, Танзания, Уганда) Восток // Афро-Азиатские общества: история и современность. — 2013. — № 1. — С. 105–118.
28. Коротаев А. В., Малков А. С., Халтурина Д. А.Компактная математическая макромодель технико-экономического и демографического развития Мир-Системы (1–1973 гг.) // История и современность. — 2007. — № 1. — С. 19–37.
29. Малафеев О. А., Зенович О. С., Севек, В. К. Многоагентное взаимодействие в динамической задаче управления венчурными строительными проектами// Экономическое возрождение России — 2012 — № 1. — С. 124–131.
30. Малафеев О. А., Пахар О. В.. Динамическая нестационарная задача инвестирования проектов в условиях конкуренции// Проблемы механики и управления: Нелинейные динамические системы — 2009 — № 41. — С. 103–108.
31. Малафеев О. А., Соснина В. В. Модель управления процессом кооперативного трехагентного взаимодействия// Проблемы механики и управления: Нелинейные динамические системы — 2007 — № 39 — С. 131–144.
32. Малафеев О. А., Черных К. С. Математическое моделирование развития компании // Экономическое возрождение России — 2004 — № 1. — С. 60.
33. Малафеев О. А., Черных К. С. Математическое моделирование развития компании// Экономическое возрождение России — 2005 — № 2. — С. 23.
34. Миндлин Ю. Б., Колпак Е. П., Балыкина Ю. Е Проблемы использования кластеров в Российской Федерации // Вестник НГУЭУ. — 2014. — № 1. — С. 22–32.
35. Михайлов А. П., Ланкин Д. Ф О конструкциях властных иерархий // Математическое моделирование. — 2009. — Т. 21. — № 8. — С. 108–120.
36. Михайлов А. П., Ланкин Д. Ф. Моделирование оптимальных стратегий ограничения коррупции // Математическое моделирование. — 2006. — Т. 18. — № 12. — С. 115–124.
37. Трубецков Д. И. Феномен математической модели Лотки-Вольтерры и сходных с ней // Известия высших учебных заведений. Прикладная нелинейная динамика. — 2011. — Т. 19. — № 2. — С. 69–88.
38. Халтурина Д., Кобзева С Геополитические перспективы России в условиях социально-демографического кризиса // Россия и мусульманский мир. — 2010. — № 2. — С. 13–20.
