Сетевые модели используются при решении различных технико-экономических задач [1…4]; имеют многочисленные приложения во всех отраслях индустриального и экономического планирования (распределение потоков товаров, газа, нефти, воды, людей и т. д.; задача о перегрузке товаров). Ограничимся рассмотрением двух наиболее важных приложений.
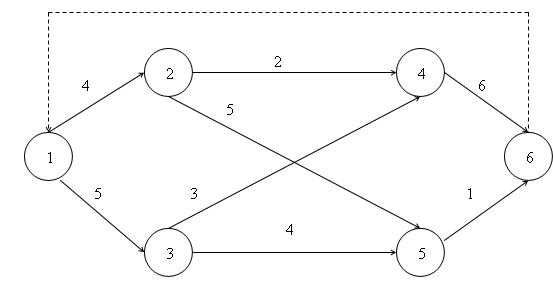
Рис.1
1. Задача о максимальном потоке. Исходные параметры задачи указаны на рис.1. Готовая продукция распределяется с минимальными расходами по складам, а оттуда попадает потребителям (источники, склады и потребители — узлы сети, пути между ними — дуги). На каждой дуге указана ее максимальная пропускная способность. Задача состоит в получении максимально возможного потока от источника (узел 1)к стоку (узел 6). Направления потоков могут быть изменены; расходы на перевозку также не учитываются. Это частный случай сетевой задачи. Неизвестными величинами являются потоки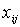 
из узла 
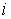в узел 
; 
, 
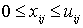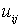- верхние пределы (пропускные способности) дуг. Из условия равновесия следует:
;
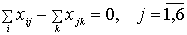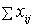- суммарный поток, поступающий в узел по всем ; 
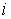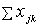- суммарный поток из -го узла по всем 
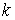. Это справедливо также для источника и стока (вводится фиктивная труба с бесконечно большой пропускной способностью (пунктир на рисунке от стока к источнику)).
Матрица инцидентности (матрица коэффициентов последнего уравнения; имеет специальную структуру):
А=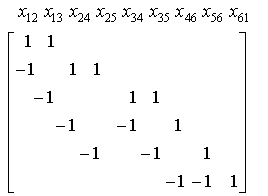
(A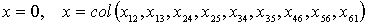
).
Каждому из шести узлов соответствует строка, и каждой из девяти дуг соответствует столбец матрицы; числа +1 и -1 полностью описывают связи между узлами и дугами. Задача определения максимального потока (сделать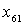 
наибольшим) превращается в обычную задачу линейного программирования (возможно использование симплекс- метода).
Укажем и другой подход (укороченный вариант). Разделим все узлы на две группы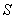 
и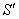 
с источником в группе 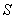и стоком в 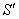(разрез сети). Сумма пропускных способностей по всем дугам, идущим из 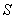в 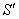, определит пропускную способность разреза (например, если 
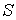содержит первый и третий узлы, то пропускная способность этого разреза равна 
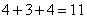; поток, превышающий 11, невозможен, так как не может пройти через разрез). Известно, максимальный поток в сети равняется пропускной способности минимального разреза (теорема о максимальном потоке и минимальном разрезе). Неравенство в одну сторону очевидно: поток не превосходит пропускной способности разреза (для произвольных значений потока и разреза). Никакой поток не в состоянии сделать больше, чем просто насытить все дуги, пересекающие разрез, и их общая пропускная способность является верхней гранью для потока (аналогично «слабой двойственности», простому неравенству 
,
, 
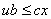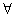
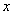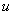). Определение достижимости равенства — более сложная задача, как и в теореме двойственности.
Пусть некоторый поток является максимальным. Рассмотрим все дуги, которые не достигли предела пропускной способности, и пусть 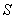содержит источник, а также все узлы, которые можно от него достичь по этим дугам. Остальные узлы образуют группу 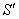. Тогда сток будет находиться в 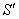; в противном случае поток не будет максимальным. Более того, каждая дуга, соединяющая 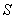с 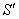, является заполненной. Иначе узел, в который она входит, принадлежал бы 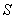, а не 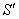. Следовательно, поток действительно наполняет разрез, и равенство достигается. Это дает возможность проверить, что заданный поток является максимальным (нужно лишь найти соответствующий разрез). В рассматриваемом примере максимальный поток равен 6 (максимальный поток и минимальный разрез указываются на рис.2). Указанная теорема дает и алгоритм решения: для любого потока нужно вычислить неиспользованную пропускную способность каждой дуги. Если сток может быть достигнут по какому-то недозаполненному пути, то следует увеличить результат. Постепенно будет достигнут максимальный поток (в случае целочисленных пропускных способностей целочисленным будет и поток — задача целочисленного программирования).
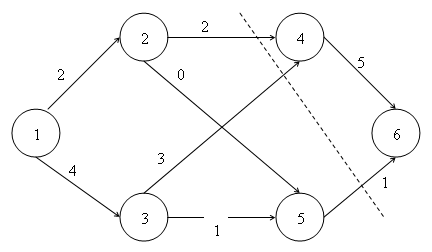
Рис. 2
2. Задача о простом назначении. В выполнении n работ участвуют m человек, каждый из которых может выполнять лишь определенные работы из указанных. Требуется распределить работы, исходя из их специальностей, не допуская при этом выполнение одной и той же работы разными людьми. Укажем необходимые условия, при которых возможно такое назначение. Каждый должен иметь, по крайней мере, одну специальность; каждая пара должна иметь две различные специальности. Каждая группа из трех (или k) человек должна быть в состоянии выполнять, по меньшей мере, три (или k) различных работ. Иначе цель не может быть достигнута. Справедливо утверждение: назначение возможно тогда и только тогда, когда каждая группа в состоянии выполнять достаточное число работ; если группа состоит из k человек, то вместе они должны быть в состоянии выполнять, по меньшей мере, k работ.
На первый взгляд условие выглядит слабым: один квалифицированный человек в состоянии помочь всей группе выполнить k работ. Однако это условие относится к каждой группе, включая и те, в которых этот человек не состоит. Если распределение работ невозможно, то всегда можно найти группу, для которой это условие выполняется. Начнем с конструирования сети, имеющей пропускную способность m между каждым человеком и работами, которые он может выполнять (исполнители подключаются к источнику, а работы — к стоку при помощи дуг с пропускной способностью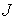 
; рис.3).
Рис.3
Если суммарный поток станет m, то все дуги от источника будут заполнены, и все будут иметь работу. Если максимальный поток окажется меньше m, то существует разрез с пропускной способностью меньше m, например, такой, что в группе S содержатся источник и узлы J1,…,Jk. j1,…jn. Ни один из этих k человек не в состоянии выполнять другие работы. Иначе нашлась бы дуга с пропускной способностью m, пересекающая разрез. Так что пропускная способность разреза равняется m-k (от источника к оставшимся людям) плюс l (от этих работ к стоку), что в сумме даст m-k+l; это величина будет меньше m при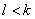 
. Следовательно, определится группа из k человек, которая может выполнять лишь 
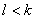работ. Если назначение окажется невозможным (поток оказался меньше m), то какая-то группа людей сдерживает его.
Приведенные сетевые модели эффективно использовались при разработке информационных моделей человека-оператора эргатической системы (как многоканальной системы управления; [5…7]).
Литература:
1. Данилов А. М., Гарькина И. А., Домке Э. Р. Математическое и компьютерное моделирование сложных систем. — Пенза: ПГУАС. — 2011. — 296 с.
2. Данилов А. М., Домке Э. Р., Гарькина И. А. Формализация оценки оператором характеристик объекта управления / Информационные системы и технологии. — 2012. — № 2. — С. 5–10.
3. Будылина Е. А., Гарькина И. А., Данилов А. М. Декомпозиция динамических систем в приложениях / Региональная архитектура и строительство. — 2013. — № 3. — С. 95–100.
4. Будылина Е. А., Гарькина И. А., Данилов А. М., Махонин А. С. Основные принципы проектирования сложных технических систем в приложениях / Молодой ученый. — 2013. — № 5. — С. 42–45.
5. Гарькина И.А, Данилов А. М., Пылайкин С. А. Транспортные эргатические системы: информационные модели и управление / Мир транспорта и технологических машин.– 2013. — № 1(40). — С.115–122.
6. Andreev A. N., Danilov A. M., Klyuev B. V., Lapshin E. V., Blinov A. V., Yurkov N. K. Information models for designing conceptual broad-profile flight simulators / Measurement Techniques. August 2000. — Vol.43. Issue 8. — P.667–672.
7. Гарькина И. А., Данилов А. М., Домке Э. Р. Математическое моделирование управляющих воздействий оператора в эргатической системе / Вестник Московского автомобильно-дорожного государственного технического университета (МАДИ). — 2011. — № 2. — С. 18–23.
