Локальная вычислительная сеть является основной частью корпоративной сети, обеспечивающей функционирование и взаимодействие различных распределенных приложений [1]. Постоянное увеличение количества подключаемых к сети узлов (рабочих и серверных станций, сетевых устройств) приводит к резкому увеличению трафика, передаваемого по магистральным сегментам, и возрастанию нагрузки на системы передачи данных. В подобной ситуации сети, построенные 3-5 лет назад, уже не справляются с возросшей нагрузкой, из-за чего снижается скорость передачи информации и теряется время при решении актуальных бизнес-задач. В результате компании несут непредвиденные финансовые потери.
Установка современных вычислительных систем не способна существенно изменить ситуацию, так как их производительность будет нивелироваться низкой пропускной способностью и сбоями сетевой инфраструктуры. Вследствие чего дорогостоящее оборудование будет использоваться лишь частично, а денежные средства, выделенные на его приобретение, окажутся потраченными впустую.
Для предотвращения подобной ситуации необходимо организовывать дополнительные каналы передачи данных сети Ethernet и использовать их для балансировки нагрузки потоков данных.
Сформулированная задача может быть разбита на следующие этапы: выявление загруженных каналов, анализ потоков трафика, оптимизация структуры сети Ethernet.
1) Выбор наиболее загруженных магистральных каналов сети Ethernet.
Пусть исходная сеть Ethernet состоит из l коммутаторов и n линий связи (магистральных портов коммутаторов). Интенсивность трафика, проходящего через коммутатор, можно представить в виде матрицы потоков F, где по строке будут представлены исходящие потоки, а по столбцу входящие потоки:
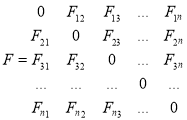,(1)
где Fij – интенсивность потока трафика от i-го порта к j-му порту.
n – количество портов коммутатора.
Чтобы избежать перегрузки коммутатора и его портов необходимо выполнение следующих условий:
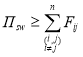,(2)
где Пsw – общая производительность коммутатора.
: 
,(3)
где Пport – общая производительность порта коммутатора.
На сегодняшний день в коммутируемых соединениях большинство линий связи работает в полнодуплексном режиме [2], поэтому для контроля загруженности канала коммутатора необходимо оценивать загрузку в каждом направлении. С каждого коммутатора, в котором реализована поддержка протокола SNMP, можно получить следующие необходимые нам данные по интерфейсам: количество интерфейсов на устройстве, их статус, скорость (биты в секунду), количество входящих и исходящих октетов на интерфейсе [3]. В результате полнодуплексный канал представляем как два симплексных канала [2], осуществляющие передачу трафика в разных направлениях (входящий и исходящий). Отсюда следует следующее условие для устойчивой работы коммутатора:
: 
,(4)
где Пsp – общая производительность симплексной линии связи (порта коммутатора, осуществляющего передачу трафика в одном направлении).
Причем, выполнение условия (4) обеспечивает выполнение условий (2) и (3).
Таким образом, для предотвращения перегрузки коммутатора и его каналов, а также контроля загруженности линий связи необходимо определить пороговое значение загрузки симплексного порта коммутатора и контролировать все потоки превышающие данное значение. Условие превышения порогового значения для j-го порта коммутатора определим следующим образом:
,(5)
где Lb – пороговое значение для j-го порта коммутатора.
Для данных, собранных в некоторые моменты времени, определим множество симплексных магистральных каналов, для которых нарушается условие (5):
(6)
В практическом плане при контроле загрузки линий связи – симплексных портов коммутаторов (СПК), нас интересует множество (6), сформулированное в отношении устойчивых высоких нагрузок. Для этого определим порог высоких нагрузок – Е, который используем для выявления высоких загрузок СПК.
Чтобы реализовать контроль превышения заданного Е разработаем алгоритм сбора и анализа загрузки СПК. Для этого определим следующие множества:
1) T = {T1 … Tp} – множество интервалов, на которых производится выборка максимальных значений загрузки СПК, при превышении порога E;
2) Ti = {Ri1 … Rim} – множество значений загрузки СПК, при превышении порога E;
3) V = {V1 … Vp} – множество маркеров превышения порогового значения загрузки Е на множестве интервалов Т.
Элементы множества V определяются таким образом, что Vi = 1, если загрузка СПК превышает установленное пороговое значение E для данного СПК, и Vi = 0 – в противном случае, то есть:
(7)
В течении всего периода контроля (опроса) рассчитываем сумму максимальных значений загрузки каждого k-го СПК – Sk, превышающих пороговый уровень E на множестве интервалов Т:
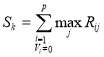(8)
А также количество интервалов – Qk, где было зафиксировано превышение порогового значения E:
(9)
В конце периода контроля (опроса) необходимо определить среднюю пиковую (максимальную) загрузку каждого k-го СПК – Zk:
(10)
В результате для каждого контролируемого СПК мы получаем среднюю пиковую загрузку и общую продолжительность превышения порога высоких нагрузок – Е, которые можно использовать для ранжирования СПК. При ранжировании каждому СПК приписывается значение, устанавливающее его относительную стоимость по отношению к другим СПК. Для этого введем таблицу приоритетов, где по строкам будут располагаться временные значения продолжительности пиковых нагрузок, а по столбцам интервалы значений загрузки СПК. Операция по заполнению таблицы приоритетов осуществляется на основе экспертных оценок [4]. Ниже приведен пример таблицы приоритетов.
Таблица 1 – Приоритеты
|
Zзначений загрузки (%) |
Qпиковых нагрузок (мин) |
|||
|
< 30 |
60 |
… |
> 120 |
|
|
> 90 |
4 |
3 |
2 |
1 |
|
80 – 90 |
5 |
4 |
3 |
2 |
|
… |
6 |
5 |
4 |
3 |
|
< 70 |
7 |
6 |
5 |
4 |
С помощью данной таблицы можно рассчитать стоимость загрузки каждого СПК.
,(11)
гдеCk – стоимость загрузки k-го СПК;
Pk – приоритет назначенный k-му СПК, согласно таблице приоритетов.
В итоге мы получаем ранжированное множество (6), которое используем, чтобы выбрать наиболее загруженные магистральные каналы для оптимизации.
2) Сбор и анализ интенсивности потоков трафика на загруженных симплексных магистральных каналах.
Прежде чем проводить оптимизацию загрузки каждого симплексного магистрального канала (СМК) из множества (6) необходимо решить следующие задачи:
А) Выявить наиболее интенсивные потоки трафика (ИПТ) из всех потоков составляющих общую загрузку СМК.
Б) Оценить необходимую пропускную способность альтернативных симплексных магистральных каналов (АСМК), на которые будут перенаправлены выявленные ИПТ.
В) Оценить насколько снизилась загрузка СМК при переносе ИПТ на АСМК.
Для решения поставленных выше задач определим алгоритм сбора и анализа интенсивности потоков трафика на СМК.
Введем следующие множества:
TF = {TF1 … TFp} – множество интервалов, на которых производится выборка средних значений интенсивности потоков трафика на СМК, в случаях, когда общая загрузка СПК превышает порог E;
TFi = {RFi1 … RFim} – множество значений интенсивности потоков трафика на СМК, в случаях, когда общая загрузка СМК превышает порог E.
Чтобы выявить ИПТ из всех потоков составляющих общую загрузку СМК необходимо произвести сбор значений устойчивых максимальных загрузок для каждого из потоков, разделяющих канал в моменты, когда общая загрузка СМК превышает установленный порог Е, – UFr:
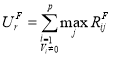(12)
В конце периода контроля (опроса) необходимо определить среднюю устойчивую максимальную загрузку для каждого из потоков разделяющих k-й СМК в моменты, когда общая загрузка превышает установленный порог Е, – WFr:
(13)
Притом значение устойчивых максимальных загрузок может вычисляться и более усредненным: на интервале TFi выбирается некоторое количество наибольших значений RFij , которые усредняются.
Таким образом, мы получаем значение устойчивой максимальной загрузки по потоку, менее подверженное влиянию флуктуаций в периоды времени, соответствующие превышению порога загрузки канала Е.
Максимальному значению UFr будет соответствовать ИПТ, вносящий наиболее существенный вклад в формирование загрузки канала в периоды превышения порога загрузки СМК.
Оценка необходимой пропускной способности АСМК, на который будет перенаправлен выявленный ИПТ производится по формулам (12) и (13), но для любых значений Vi, т.е. сбор и анализ значений RFij осуществляется на протяжении всего периода контроля. Значение WFr , полученное для любых значений Vi будет являться минимальной необходимой пропускной способностью АСМК.
Оценку насколько снизилась загрузка СМК при переносе ИПТ на АСМК необходимо проводить следующим образом:
В течении всего периода контроля (опроса) рассчитываем сумму средних значений загрузки для каждого r-го потока – SFr, в случаях, когда общая загрузка СМК превышает порог E на множестве интервалов ТF:
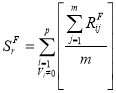,(14)
где m – количество опросов на интервале Ti.
В конце периода контроля (опроса) необходимо определить среднюю загрузку для r-го потока k-го СМК – ZFr:
(15)
Таким образом, при переносе r-го потока с k-го СМК на АСМК, загрузка k-го СМК в среднем уменьшится на величину ZFr .
В результате мы получаем потоки данных в каждом симплексном магистральном канале, ранжированные по степени влияния на общую загрузку канала в моменты времени, соответствующие высокой загрузке канала и оценку снижения загрузки на СМК при переносе ИПТ на АСМК.
3) Алгоритм оптимизации структуры сети Ethernet с точки зрения загруженности магистральных линий связи.
Получив ранжированное множество (6) и ранжированные по степени влияния на загрузку канала ИПТ можно приступить к оптимизации структуры сети Ethernet, начиная с самой загруженной магистральной линии связи (ЗМЛС). Оптимизацию будем проводить путем организации дополнительных линий связи в сети Ethernet, на которые будем направлять наиболее интенсивные потоки трафика с ЗМЛС.
Рассмотрим систему из n каналов, в каждом из которых циркулирует m потоков данных (такое допущение возможно в силу того, что для каждого канала можно определить набор из m потоков, вносящих наибольшую долю в загрузку канала). Здесь рассматриваются каналы коммутаторов как симплексные, осуществляющие передачу данных в исходящем направлении, так как согласно матрице потоков (1), мы имеем информацию из каких потоков (потоков с каких интерфейсов) сформирован исходящий поток. То есть при рассмотрении выявленной ЗМЛС соединяющей коммутатор А с коммутатором Б, сначала рассматриваем исходящий поток от коммутатора А к коммутатору Б, а потом входящий, только представленный как исходящий поток от коммутатора Б к коммутатору А. Таким образом, учитываем полнодуплексный режим выявленной ЗМЛС.
Все ЗМЛС из множества (6) объединим в группы, у которых общая загрузка превышает порог E в одни и те же промежутки времени. Такие группы могут быть построены путем анализа множеств V, определенных для каждого из ЗМЛС.
Каналы и потоки пронумерованы в порядке уменьшения их загрузки (пункты 1 и 2), то есть каналу номер 1 соответствует максимальное значение загрузки.
Пусть Li1 – значение устойчивой высокой загрузки i-го канала;
FijA – значение средней загрузки j-го потока, проходящего через i-й канал;
FijM – значение устойчивой высокой загрузки j-го потока, проходящего через i-й канал;
Lik – рассчитанное значение ожидаемой устойчивой высокой загрузки i-го канала на k-м (k>0) шаге алгоритма оптимизации.
На первом шаге алгоритма изымаем первый поток (наиболее интенсивный) из первого канала (самого загруженного): 
.
Далее организуем виртуальный канал под изъятый поток с минимальной пропускной способностью равной значению устойчивой высокой загрузки 1-го потока, проходящего через 1-й канал:
. Организованный виртуальный канал соединяет узлы сети, между которыми протекает интенсивный (1-й изъятый) поток.
В случае если рассматриваемый канал является частью полнодуплексной линии связи, то также изымаем поток, направленный в противоположном направлении.
Теперь проверяем условие: если L11 < E , то переходим к следующему каналу, иначе изымаем второй наиболее интенсивный поток из данного канала:
. Для изъятого потока организуем новый виртуальный канал: 
и снова проверяем условие: если L12 < E , то переходим к следующему каналу, иначе изымаем следующий наиболее интенсивный поток из данного канала:
и т.д.
Таким образом, на k-м шаге алгоритма изымаем наиболее интенсивный j-й поток, где 
из i-го канала:
(16)
Для изъятого потока организуем новый виртуальный канал с минимальной пропускной способностью равной значению устойчивой высокой загрузки изъятого потока:
(17)
Завершающим этапом данного шага является проверка следующего условия:
(18)
Если условие (18) выполняется, то на следующем шаге алгоритма (k+1) переходим к следующему каналу (i+1), иначе на следующем шаге алгоритма (k+1) изымаем следующий наиболее интенсивный j-й поток из рассматриваемого i-го канала по формуле (16) и т.д.
Особым случаем при разгрузке k-го канала является существование «соседнего» виртуального канала. Тогда, если существует ИПТ, который может быть использован для разгрузки данного канала и проходит через канал передачи данных в текущей временной группе, для которого в ходе работы алгоритма уже выделен виртуальный канал и выполняется условие:
,(19)
где Lвирт – загрузка виртуального канала.
Вместо (16), (17), (18) используем:
(20)
и перестраиваем виртуальный канал следующим образом: изменяем узел-получатель виртуального канала на узел, являющийся получателем для рассматриваемого канала. Что равносильно, в случае использования представления сети в виде матрицы смежности для соответствующего графа [5] переносу значения загрузки для рассматриваемого виртуального канала в элемент матрицы с индексами (x, i), где i – номер канала разгружаемого на текущем шаге алгоритма, х – узел источник для виртуального канала. Таким образом, мы учитываем влияние ИПТ на несколько смежных ЗМЛС в пределах одной временной группы.
В результате на каждом k-м шаге алгоритма получаем вариант оптимизации структуры сети Ethernet путем организации дополнительных каналов связи с устойчивыми высокими загрузками Ln+k и значение ожидаемой устойчивой высокой загрузки для рассматриваемого канала. В конце работы алгоритма имеем список виртуальных каналов, реализовав которые получаем оптимизированную с точки зрения загруженности структуру сети Ethernet, где для каждого i-го канала связи не превышается порог загрузки E: Li < E. При этом список составлен в порядке приоритетов согласно экспертным оценкам, заданным таблицей приоритетов.
Литература:
1. Амато Вито, Основы организации сетей Cisco / Амато Вито. – М.: Издательский дом "Вильямс", 2004. – 464 с.
2. Куин Л. Fast Ethernet / Л. Куин, Р. Рассел. – К.: Издательская группа BHV, 1998. – 448 с.
3. Потуремский И.В. Система анализа и мониторинга загрузки сегментов локальной вычислительной сети / Вестник НИИ СУВПТ - Вып. 26. Красноярск: НИИ СУВПТ, 2008, с. 98-105.
4. Орлов А.И. Экспертные оценки. Учебное пособие. [Электронный ресурс] / А.И. Орлов. – Москва: 2002. Режим доступа: http://orlovs.pp.ru/stat/expert.zip.
5. Харари Ф. Теория графов 2-е изд. / Ф. Харари. – М.: Едиториал УРСС, 2003. – 296 с.
