In the present paper we consider a 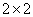 operator matrix acting in the direct sum of zero-particle and one-particle subspaces of Fock space. It is shown that this operator has no more than one positive and no more than two negative simple eigenvalues.
operator matrix acting in the direct sum of zero-particle and one-particle subspaces of Fock space. It is shown that this operator has no more than one positive and no more than two negative simple eigenvalues.
Keywords: Operator matrix, Fock space, eigenvalue, annihilation and creation operators, polynom, essential and discrete spectrum.
Block operator matrices are matrices the entries of which are linear operators between Banach or Hilbert spaces. Such operators often arise in mathematical physics, e.g. in fluid mechanics (see [1]), magnetohydrodynamics (see [2]) and quantum mechanics (see [3]). Spectral properties of the block operator matrices are studied in detail in [4]. One of the special class of block operator matrices are Hamiltonians associated with a system describing 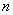 -particles in interaction without conservation of the number of particles. Here off-diagonal entries of such block operator matrices are annihilation and creation operators. The study of systems describing
-particles in interaction without conservation of the number of particles. Here off-diagonal entries of such block operator matrices are annihilation and creation operators. The study of systems describing 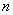 -particles in interaction without conservation of the number of particles is reduced to the study of the spectral properties of self-adjoint operators acting in the zero-particle, one-particle,…,
-particles in interaction without conservation of the number of particles is reduced to the study of the spectral properties of self-adjoint operators acting in the zero-particle, one-particle,…, 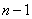 -particle subspaces of a Fock space.
-particle subspaces of a Fock space.
In the present paper we consider a 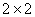 block operator matrix acting in the direct sum of zero-particle and one-particle subspaces of a Fock space. We prove that this operator has no more than one positive and no more than two negative simple eigenvalues.
block operator matrix acting in the direct sum of zero-particle and one-particle subspaces of a Fock space. We prove that this operator has no more than one positive and no more than two negative simple eigenvalues.
Let 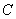 be the field of complex numbers and
be the field of complex numbers and 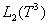 be the Hilbert space of square integrable (complex) functions on
be the Hilbert space of square integrable (complex) functions on 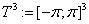 . Denote by
. Denote by 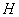 the direct sum of spaces
the direct sum of spaces 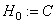 and
and 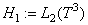 , that is,
, that is, 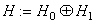 . The spaces
. The spaces 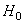 and
and 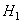 are zero- and one-particle subspaces of a Fock space
are zero- and one-particle subspaces of a Fock space 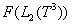 over
over 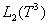 , respectively.
, respectively.
Let us consider the following 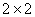 operator matrix
operator matrix 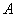 acting in the Hilbert space
acting in the Hilbert space 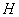 as
as
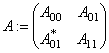 ,
,
where the entries 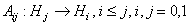 are defined by
are defined by
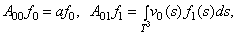
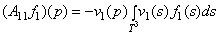 .
.
Here 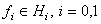 ;
; 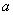 is a fixed read number, the functions
is a fixed read number, the functions 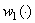 and
and 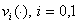 are real-valued continuous functions on
are real-valued continuous functions on 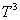 and
and 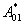 denotes the adjoint operator to
denotes the adjoint operator to 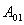 .
.
Under this assumptions the operator 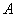 is bounded and self-adjoint in
is bounded and self-adjoint in 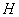 .
.
We remark that the operators 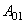 and
and 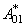 are called annihilation and creation operators, respectively.
are called annihilation and creation operators, respectively.
We denote by 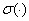 ,
, 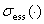 and
and 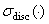 the spectrum, essential spectrum and discrete spectrum of a bounded self-adjoint operator.
the spectrum, essential spectrum and discrete spectrum of a bounded self-adjoint operator.
Lemma 1. The relation holds.
Proof. Since the operator 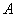 is a bounded self-adjoint operator whose rank does not exceed three, we have . We show that . To this end, we consider the equation
is a bounded self-adjoint operator whose rank does not exceed three, we have . We show that . To this end, we consider the equation 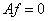 for
for 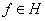 , which is equivalent to the system of equations
, which is equivalent to the system of equations
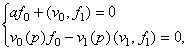 (1)
(1)
where 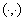 is the scalar product in
is the scalar product in 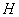 . It is easy to see that the elements of the subspace
. It is easy to see that the elements of the subspace
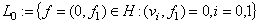
are solutions of system of equations (1). Then the fact 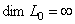 implies that . The lemma is proved.
implies that . The lemma is proved.
By Lemma 1 the operator 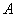 may have only positive and negative discrete eigenvalues. The following theorem describes the number and location of these eigenvalues.
may have only positive and negative discrete eigenvalues. The following theorem describes the number and location of these eigenvalues.
Theorem 1. The operator 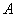 has no more than one positive and no more than two negative simple eigenvalues.
has no more than one positive and no more than two negative simple eigenvalues.
Proof. Let us consider the equation 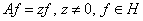 or the system of equations
or the system of equations
 . (2)
. (2)
Since 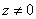 from the second equation of (2) we find
from the second equation of (2) we find
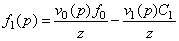 , (3)
, (3)
where
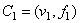 . (4)
. (4)
Substituting the expression (3) for 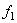 into the first equation of the system of equations (2) and the equality (4) we have that the system of equations (2) has a solution if and only if
into the first equation of the system of equations (2) and the equality (4) we have that the system of equations (2) has a solution if and only if
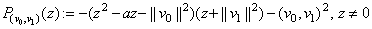 ,
,
where 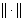 is the norm in
is the norm in 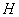 .
.
We note that, if 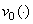 and
and 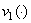 are linear dependent, then
are linear dependent, then 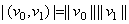 . Therefore,
. Therefore,
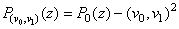
and
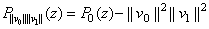 .
.
By the inequality 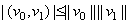 we obtain that
we obtain that
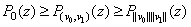 .
.
There are three cases are possible: 1) 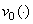 and
and 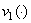 are orthogonal; 2)
are orthogonal; 2) 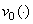 and
and 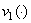 are parallel; 3)
are parallel; 3) 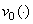 and
and 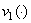 are neither orthogonal and nor parallel.
are neither orthogonal and nor parallel.
Let 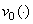 and
and 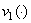 be orthogonal. Then
be orthogonal. Then
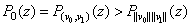 .
.
In this case the numbers
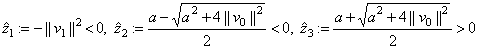
are zeroes of 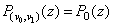 , i.e., the eigenvalues of
, i.e., the eigenvalues of  .
.
We remark that the numbers 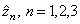 are also zeroes of
are also zeroes of 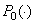 in the case where
in the case where 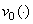 and
and 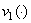 are not orthogonal.
are not orthogonal.
Let 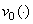 and
and 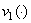 be parallel. Then
be parallel. Then
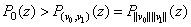 .
.
In this case the polynomial 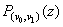 can be written in the form
can be written in the form
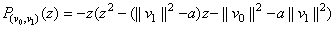 .
.
For convenience we assume that 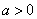 . From here it follows that the numbers
. From here it follows that the numbers
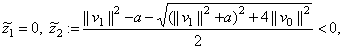
and
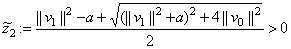
are zeroes of 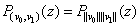 , i.e., the eigenvalues of
, i.e., the eigenvalues of 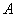 . In the case where
. In the case where 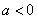 we have
we have 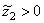 and
and 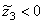 .
.
We remark that the numbers 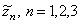 are also zeroes of
are also zeroes of 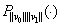 in the case where
in the case where 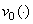 and
and 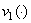 are not parallel.
are not parallel.
Let 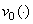 and
and 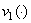 be neither orthogonal and nor parallel. Then
be neither orthogonal and nor parallel. Then
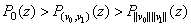 .
.
Set  and
and 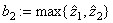 . Without loss of generality (otherwise we would be prove the following facts in the same way) we assume that the inequalities
. Without loss of generality (otherwise we would be prove the following facts in the same way) we assume that the inequalities 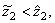
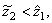
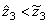 hold. Then it follows that
hold. Then it follows that 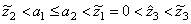 . Since the numbers
. Since the numbers 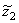 and
and 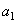 are zeroes of
are zeroes of 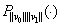 and
and 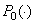 , respectively, we have
, respectively, we have
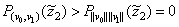
and
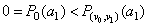 ,
,
i.e. on the boundary of 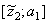 the polynomial
the polynomial 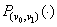 has a different sign. Hence, there exists a point
has a different sign. Hence, there exists a point 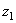 , such that
, such that 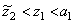 and
and 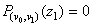 . Analogously one can prove that there exist the numbers
. Analogously one can prove that there exist the numbers 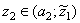 and
and 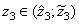 , which are zeroes of the polynomial
, which are zeroes of the polynomial 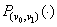 .
.
Since 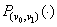 is a polynomial of degree 3 these zeroes are simple.
is a polynomial of degree 3 these zeroes are simple.
One can see that 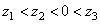 . Theorem 1 is completely proved.
. Theorem 1 is completely proved.
Notice that Theorem 1 plays important role in the study the number of eigenvalues corresponding generalized Friedrichs model.
References:
1. S. Chandrasekhar. Hydrodynamic and hydromagnetic stability. The International Series of Monographs on Physics. Clarendon Press Oxford University Press, New York, 1998. Reprint of the 1992 edition.
2. E. Lifschitz. Magnetohydrodynamic and spectral theory. Vol. 4 of Developments in Electromagnetic Theory and Applications. Kluwer Academic Publishers Group, Dordrecht, 1989.
3. Thaller. The Dirac equation. Texts and Monographs in Physics. Springer, Berlin, 1992.
4. Tretter. Spectral theory of block operator matrices and applications, Impe. Coll. Press, 2008.

