Different types of features in the description of objects does not allow to use as a tool for the study of methods of statistical exploratory data analysis. To solve this problem it is offered to use the methods of data mining oriented on search of the hidden regularities in databases.
One of the directions of the intellectual analysis is classification. The considerable volume of information at the solution of problems of classification represents knowledge for structural placement of class objects and complexity of a configuration in borders of classes.
Data on structural placement of objects of classes in feature space for a given metric. we tried to get a variety of ways.. For example, about complexity of a configuration in borders of classes it was possible to judge by results of correct recognition of objects by means of linear, piecewise and linear decision functions [1]. Another feature was the use of structural stability of the objects in the disjoint classes. The problem of calculating the stability of a variety of structural measures are being considered within the framework of nonparametric methods of recognition.
Stability shows the local properties in the sample of classified objects. Knowledge of these properties is necessary to determine the anomalous object classes, explaining the reasons for choosing the objects of the minimum coverage standards of learning sample, sufficient for its correct recognition.
The variety value of stability of objects of classes in [4] depended on the choice of the metric. As in polytypic feature space there are no proximity measures with properties of a metrics, it was necessary to use different approaches. Thus, the structural characteristics of the placement of each of the ethalon objects locally and optimal coverage 
class training sample in artificial neural networks (ANN) with minimal configuration was calculated through a share incorrectly recognized objects during the exam on a set of a moving 
. The solution of a problem of an estimstion of stability and algorithmic (without the participation of experts) ranking objects of classes on generalized estimates in heterogeneous feature space had not previously considered.
Statement of the problem
We consider the problem of recognition in the standard formulation. It is believed that given a set of objects 
containing representatives l disjoint classes 
. Description of objects is performed using a set of n different types of features 
, 
of which are measured in nominal scale, 
on an interval scale.
It is required to compare the stability of objects in a given data and after the preprocessing.
For each 
construct a sequence 
objects E
ordered with increasing distance 
from the 
metric and allocation of set of boundary pairs
, 
,
formed from the inequalities
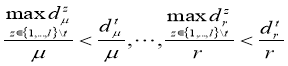
where 
(
) — the number of objects from 
nearest 
, belonging to the class 
, 
. Objects of class 
make a relative majority for any integer 
nearest objects to 
.
The value of functionality F(k) is determined by quantity of the executed inequalities 
by a set of boundary pairs of 
of each object 
, (
).
Stability of object of 
on a metrics of 
is calculated as
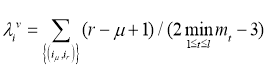
and class
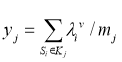
Computational experiment.
To illustrate the process visualization objects was used «Korean» [1] data (which is taken from sociology fields). The set is represented 100 objects with 24 nominal features. Objects are divided into two disjoint classes, K1 (Uzbek people), K2 (Korean people). Results of stability of the objects in a given data are presented in Table1.
Table 1
Stability of the objects in agiven data
|
Number of Object |
Stability |
|
54 |
1.00 |
|
19 |
1.00 |
|
1 |
1.00 |
|
30 |
0.57 |
|
74 |
0.53 |
|
100 |
0.44 |
|
95 |
0.00 |
|
87 |
0.00 |
|
83 |
0.00 |
According to Table1 average stability of the first class and second class are equal to 0.74 and 0.69 respectively. Anomalous objects are located in the bottom of the tablle and is choosen according to the low stability. Anomalous objects are presented in Table 2.
Table 2
List of Anomalous objects
|
Number of object |
|
95 |
|
87 |
|
83 |
|
57 |
|
45 |
|
23 |
|
84 |
|
53 |
|
49 |
|
75 |
|
15 |
|
10 |
We perform preprocessing through the changing of the classes of anomalous objects. Result for stability of the objects after the preprocessing are presented in Table 3.
Table 3
Stability of the objects after the preprocessing
|
Number of Object |
Stability |
|
54 |
1.00 |
|
19 |
1.00 |
|
1 |
0.94 |
|
30 |
0.90 |
|
74 |
0.98 |
|
100 |
0.99 |
|
95 |
0.92 |
|
87 |
0.86 |
|
83 |
0.93 |
Conclusion.
As we can see in above tables, stabilities of features were better after the preprocessing. For instance the stabilities of 95th and 85th objects were 0.00 in Table1 and it changed to 0.92 and 0.93 respectively. Although the stability of first object decreased average stability of the first class and second class were equal to 0.87 and 0.92 respectively. It means anomalous objects are nearer to other class objects than their class.
References:
- Knowledge Discovering from Clinical Data Based on Classification Tasks Solving / N. A. Ignat'ev, F. T. Adilova, G. R. Matlatipov, P. P. Chernyш // MediNFO. — Amsterdam: IOS Press, 2001. — P. 1354–1358.
- Игнатьев Н. А. Выбор минимальной конфигурации нейронных сетей // Вычислительные технологии. – Новосибирск, 2001. – Т. 6, № 1. – С. 23-28.
- Игнатьев Н. А. Интеллектуальный анализ данных на базе непараметрических методов классификации и разделения выборок объектов поверхностями. – Ташкент, 2008. – 108 с.
- Игнатьев Н. А. Обобщенные оценки и локальные метрики объектов в интеллектуальном анализе данных // Монография. – Ташкент: Национальный университет Узбекистана им. МирзоУлугбека, 2014. — 71 с.
- Wold S. Pattern recognition by means of disjoint principal components models // Pattern Recognition, 8, № 3, 1976, 127–139.
