We study the fractionally loaded heat equation with a load as a Riemann-Liouville derivative with respect to the time variable. The study of set boundary value problem is concluded with obtaining the integral equation. Also, we checked the limit cases for the fractional order derivative in the heat equation of BVP. It could be seen that the order of the fractional derivative is crucial in stating the existence and uniqueness of solutions.
Keywords :heat equation, fractional Riemann-Liouville derivative, Volterra integral equation.
1 Introduction
The differential theory and fractional integration have been developing thanks to their application in different fields of science. Noticeably, the fractional derivative study has been done actively in previous decades [1–4]. The interest in its study develops to grow too now [5–7]. Application of fractional derivatives, especially of Riemann-Liouville type, has been used in physics problems which involve impulses. The study of existence of higher order derivatives has been done in [5]. This paper is about a boundary value problem of a heat equation with the fractional load. The load is a Riemann-Liouville fractional derivative of the first order. Using the general solution obtained from [10] and manipulating through the solution the original problem has been reduced to a Volterra integral equation of a second kind with a kernel of degenerated hypergeometric Tricomi function. Later the limiting cases in the [0,1] interval it was proven that solution in the boundary values correspond to the kernel of the function.
2 Background definitions and concepts
It is better to revise some defined notions and concepts. Let us start from the definition of the fractional derivative of Riemann-Liouville type.
Definition 2.1
Let
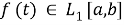
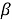
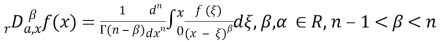
For
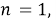
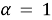
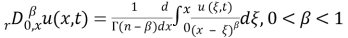
In addition, these following special functions are used during this paper:
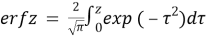
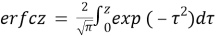
Definition 2.2 Linear independent solutions of the equation
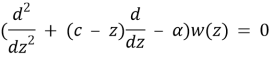
are functions
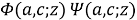
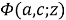
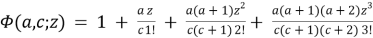
and
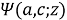
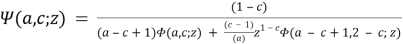
Tricomi degenerate hypergeometric function can be represented as an integral [9]:
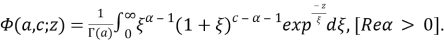
For large
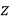
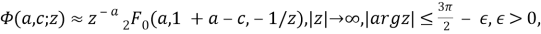
where
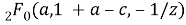
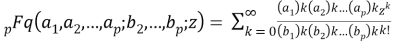
where
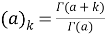
is the Pohammer symbol. Theory of differential equations with fractional derivatives has been a pivot point in the study of fractional calculus. Firstly, we will use the method of integral equations where the boundary values are brought down in two integral equations with transformed Kernel.
We also in this paper use a method to contemplate on our problem by reducing the differential part into integral equation. It was proven that in the domain
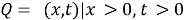
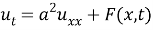
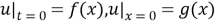
is described by the formula
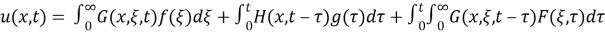
where
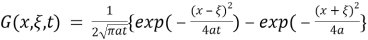
It will be seen further that the first and second terms in the equation (4) are equal to zero in correspondence with boundary values. So, then we will be left only with the third term, where
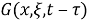
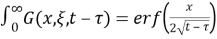
3 Statement of the problem
In the domain
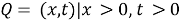
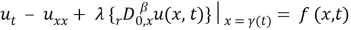
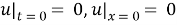
where
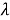
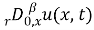
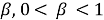
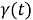
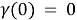
4 Reducing the boundary value problem to an integral equation
Lemma 4.1. The boundary value problem (6)-(7) is equivalently reduced to Volterra integral equation of the second kind with a kernel that contains a special function.
Proof. Let
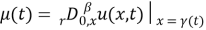
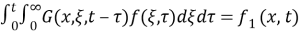
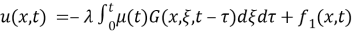
Then we take the fractional derivative of
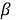
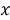
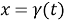
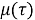
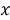
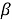
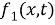
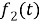
Thus (8) becomes as the following as we insert (5):
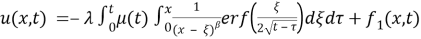
We calculate the derivative and by interchanging the integrals:
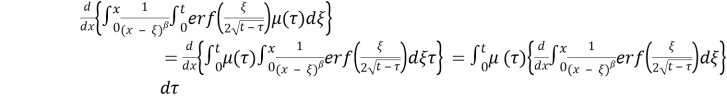
We introduce a new variable
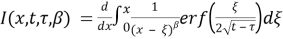
Then we rewrite the (10):
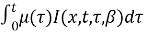
By change of the variable, we can solve
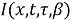
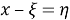
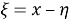
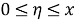
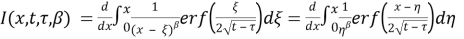
By taking the partial derivative:
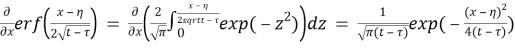
Hence, we will have:
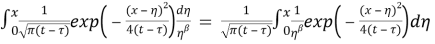
By substituting
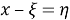
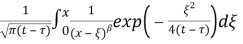
By using Gradstein’s solutions [8],
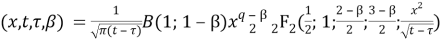
here
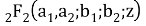
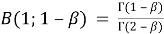
Then
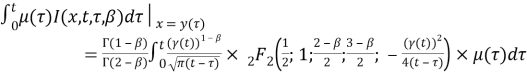
Then (8) becomes:
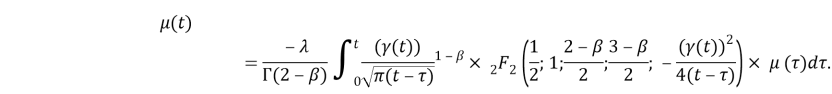
Then in such way BVP (6)-(7) is reduced to the following integral equation:
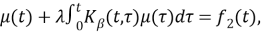
where
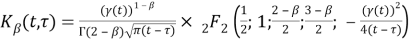
5 Study the boundary points of the changing interval of derivative order
Lemma 4.1.
For boundary value problem (6)-(7) there is a continuity in the order
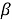
Proof. The boundary points of our problem (7) are considered. Now we check the boundary points of
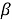
-
When
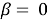
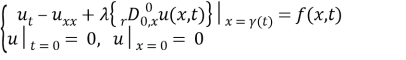
where
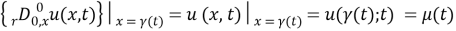
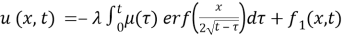
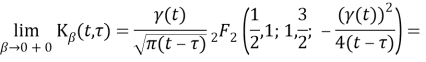
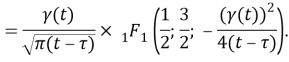
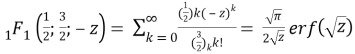
where
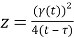
Hence,
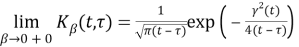
So,
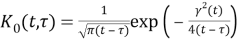
II. Now, for a case

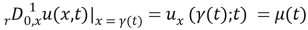
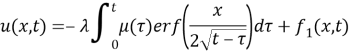
And then by taking the derivative w.r.t.
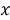
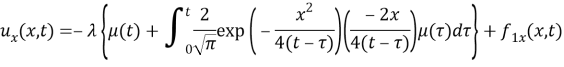
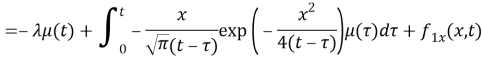
As we defined
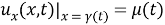
The equation becomes
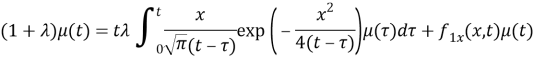
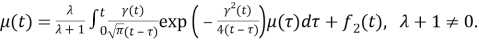
If
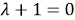
The Kernel of (14) has the form:
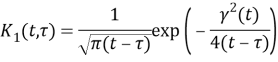
In another hand, by taking the limit from (12), we obtain:
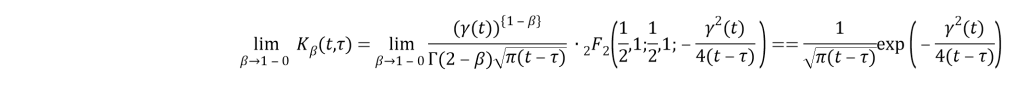
When

6 Conclusion
Covered by theorems` s statement, kernel (12) of the integral equation has a weak singularity. Consequently, to find an unique solution to the equation (11) in the class of continuous functions, it is possible to apply method of successive approximations. Natural classes of functions are well-pose homogenous boundary value problems.
In case when ω ≥ 21 and ω ≥ 1 − 2β when 0 ≤ β ≤ 1 for
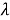
References:
1. Samko, S. G., Kilbas, A. A., & Marichev, O. I. (1993). Fractional Integrals and Derivatives. Theory and Application. Gordon and Breach: New York, 1006 p.
2. Le Mehaute, A., Tenreiro Machado, J. A., Trigeassou, J. C., & Sabatier, J. (2005). Fractional Differentiation and its Applications. Bordeaux Univ: Bordeaux.
3. Podlubny, I. (2002). Geometric and physical interpretation of fractional integration and fractional differentiation. Fract. Calculus Appl. Anal., 5, 367–386. an: 1042.26003.
4. Heymans, N., & Podlubny, I. (2006). Physical interpretation of initial conditions for fractional differential equations with Riemann-Liouville fractional derivatives. Rheologica Acta, 45 (5), 765–772. DOI: 10.1007/S00397–005–0043–5.
5. Feng, M., Zhang, X., & Ge, W. (2011). New existence results for higher-order nonlinear fractional differential equations with integral boundary conditions. Bound. Value Probl. Art., 720702, 20 pp. DOI: 10.1155/2011/720702.
6. Cao Labora, Daniel, Rodriguez-Lopez, Rosana, & Belmekki, Mohammed. (2020). Existence of solutions to nonlocal boundary value problems for fractional differential equations with impulses. Electronic Journal of Differential Equations, 15, 16 pp.
7. Yusuf, A., Qureshi, S., Inc, M., Aliyu, A.I., Baleanu, D., & Shaikh, A.A. (2018). Two-strain epidemic model involving fractional derivative with Mittag-Leffler kernel. Chaos: An Interdisciplinary Journal of Nonlinear Science, Vol. 28, Iss. 12, 28 pp. 123121. DOI: 10.1063/1.5074084.
8. Gradshteyn, I.S., & Ryzhik, I.M. (2007). Table of Integrals, Series, and Products. AP: New York. USA. 7 edition, 1171 p.
9. Prudnikov, A. P., Brychkov, Yu. A., & Marichev, O. I. (1989). Integrals and Series: More Special Functions. Vol. 3. Gordon and Breach: New York-London. 808 p
10. Polyanin, A.D. (2002). Handbook of Linear Partial Differential Equations for Engineers and Scientists. Chapman and Hall/CRC: New York-London. 780 p.

