Алгоритм сокращения стояночного времени судна, находящегося под обработкой в порту

Одной из важнейших проблем в области повышения экономической эффективности водного транспорта является сокращение стояночного времени судов в портах. Сокращение стоянки судов может быть достигнуто за счет проведения целого комплекса организационно-технических мероприятий, направленных как на улучшение обслуживания судов в портах, так и на интенсификацию погрузо-разгрузочных работ.

Рассматривается задача составления расписания в следующей постановке. Прибывшее в порт грузовое судно, с порожними трюмами необходимо загрузить двумя видами грузов: листовой сталью и круглым лесом. Обработку необходимо произвести в такой последовательности, при которой суммарное время нахождения судна у причальной стенки под обработкой было бы минимальным. Погрузка осуществляется портальным краном и колёсным экскаватором с грейфером. Портальный кран выполняет операцию по погрузке листов в трюмы, а экскаватор укладывает лес на палубу над трюмами.

Предположим, что для погрузки листов в i-й трюм необходимо время t_i, а для укладки леса над i-ым трюмом время t_i(i= 1, 2 …, N, где N — число трюмов). Операция по укладке леса на палубу над i-ым трюмом может выполняться только после завершения загрузки i-го трюма. Поэтому в начальный момент (до окончания работы портального крана) экскаватор простаивает. Простои экскаватора будут зависеть от выбранной очередности обработки трюмов, осуществляемой портальным краном.

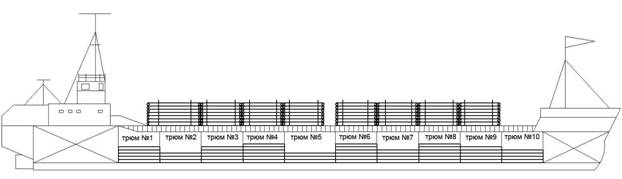
Рис.1. Схема размещения грузов в трюмах и на палубе судна

Предположим, что портальный кран приступает к погрузке очередного трюма непосредственно после завершения работы на предшествующем, т. е. работает без перерывов. Очевидно, условия работы экскаватора не оказывают влияния на портальный кран. В общем случае время грузовых операций может быть представлено в виде множества, состоящего из пар чисел:

t1, t1

t2, t2

……

tN, tN.

Время обработки судна изменяется в зависимости от выбранной перестановки. Если, например, N=3 и пары чисел имеют значения

t1=5, t1=3,

t2=4, t2=6,

t3=7, t3=4,

то время обработки судна åi для различных перестановок будет равно:

å1=f(t1, t2, t3)=20

å2=f(t1, t3, t2)=22

å3=f(t2, t1, t3)=20

å4=f(t2, t3, t1)=19

å5=f(t3, t1, t2)=22

å6=f(t3, t2, t1)=20.

Оптимальным решением является перестановка, соответствующая å4=19.

Если х_i — время простоя экскаватора перед тем, как будет завершена работа портального крана по погрузке i-го трюма, то для минимизации простоев экскаватора следует найти минимум из всех максимальных значений, определенных рекуррентными соотношениями:

,

,

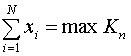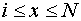где

.

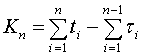С этой целью может быть использован следующий алгоритм перестановки.

1.                       Записать исходные данные t_i, t_i, i=1 …, N в виде двух столбцов с соответствующей начальной нумерацией.

2.                       Определить среди чисел t_i, t_i наименьшее. Если таковым окажется t_i — выполнять эту операцию первой. Если таким числом является t_i — обрабатывать i-ый трюм необходимо последним.

3.                       Исключить из дальнейшего рассмотрения i-ую группу чисел и продолжить работу с оставшимися числами, согласно п. п. 1 и 2 алгоритма.

4.                       При наличии нескольких минимальных чисел — выбрать группу с меньшим номером. Если t_i = t_i, упорядочивать последовательность обработки трюмов по значению t_i.

Ниже приведена программа для реализации алгоритма в среде MatLAB.

% sah2a.m

% Составление оптимального расписания выполнения погрузочных работ.

% Исходные данные представлены матрицей АА (время выполнения грузовых операций

% в относительных единицах). Первый столбец АА — время погрузки в %трюмы листовой стали, второй столбец -время погрузки лесоматериалов). Номер

% строки соответствует номеру трюма (см. рис.1)

AA=[ 0.0153  0.5028;

          0.4451  0.4289;

            0.9318  0.3046;

            0.4660  0.1897;

            0.4186  0.1934;

            0.8462  0.6822;

            0.5252  0.3028;

            0.2026  0.5417;

            0.6721  0.1509;

            0.8381  0.6979];

A=AA

L=size(A); N=L(1)

Za=[]; Zb=[];

for I=1 : L(1)-1;

[z1,I1]=min(A(:,1)); [z2,I2]=min(A(:,2));

S=[ ];

if z2<z1

            ab1=A(I2, :);

            Zb=[Zb;ab1];

s=I2;

elseif z1<=z2

            ab2=A(I1,:);

            Za=[Za;ab2];

            s=I1;

            end

S=[S s];  k=S;

A1=[A(1:k-1,:); A(k+1:N-I+1,:)];

A=A1;

Za;

Zb;

S=[ ];

end

A1;

Zb1=flipud (Zb);

Aopt = [Za;A1;Zb1]

v = 1:N;

plot (v,Aopt(:,1),'*',v,Aopt(:,2),'o'),grid

Решение

A =[ 0.0153    0.5028

        0.4451    0.4289

        0.9318    0.3046

        0.4660    0.1897

        0.4186    0.1934

        0.8462    0.6822

        0.5252    0.3028

        0.2026    0.5417

        0.6721    0.1509

        0.8381    0.6979]

N = 10.Работа программы завершается графическими построениями. Для оптимальной перестановки t_i на графике представляются знаком “ * ”, а время t_i — знаком “o”.

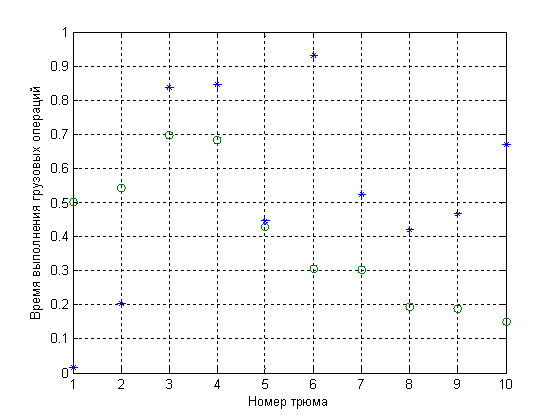
Рис.2 Оптимальное расписание обработки судна

В заключение приведена оптимальная перестановка, выполненная с помощью описанной выше программы и являющаяся, по существу, расписанием, соответствующим минимуму времени обработки судна.

С помощью алгоритма обеспечивается расчет минимума стояночного времени судов под обработкой, что способствует повышению экономической эффективности их использования и улучшению технологии работы перегрузочных средств порта.