Рассматривается приложение методов корреляционного и спектрального анализа к обработке данных при проектировании и эксплуатации сложных систем (строительные конструкции, тренажные и обучающие комплексы для подготовки операторов эргатических систем в различных отраслях промышленности и др. [1…3]); приводится алгоритм, прошедший апробацию при проектировании мобильных систем различного назначения. Обычно используется описание сигналов функциями частоты (в виде суммы более простых сигналов). Переход в частотную область осуществляется по преобразованию Фурье:
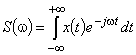 ,
,
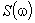 — спектральная функция или спектральная плотность (комплексная функция, имеет размерность сигнала, умноженную на время;
— спектральная функция или спектральная плотность (комплексная функция, имеет размерность сигнала, умноженную на время; 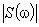 - спектр амплитуд,
- спектр амплитуд, 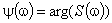 - спектр фаз). Функцию
- спектр фаз). Функцию 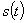 можно рассматривать как сумму бесконечного ряда гармонических составляющих с амплитудами
можно рассматривать как сумму бесконечного ряда гармонических составляющих с амплитудами 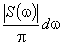 , непрерывно заполняющими интервал частот от 0 до
, непрерывно заполняющими интервал частот от 0 до 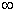 , и начальными фазами
, и начальными фазами 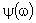 ; представление
; представление 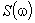 функции
функции 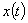 в частотной области позволяет легко установить ее физический смысл.
в частотной области позволяет легко установить ее физический смысл.
При проектировании и эксплуатации сложных конструкций часто используются анализаторы спектров, отличающиеся, в основном, лишь по диапазону частот (низко- и широкополосные, оптического диапазона), по принципу действия (многоканальные и сканирующие), по способу обработки (аналоговые и цифровые), по характеру анализа (скалярные и векторные). Они позволяют определить амплитуду и частоту спектральных компонент, входящих в состав анализируемого процесса. Важнейшей характеристикой анализатора спектра является разрешающая способность (наименьший интервал 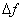 по частоте между двумя спектральными линиями, которые ещё разделяются анализатором спектра). Истинный спектр можно получить лишь тогда, когда анализируемое колебание
по частоте между двумя спектральными линиями, которые ещё разделяются анализатором спектра). Истинный спектр можно получить лишь тогда, когда анализируемое колебание 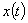 периодично, либо существует только в пределах интервала
периодично, либо существует только в пределах интервала 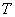 . Анализатор позволяет получить не истинный спектр
. Анализатор позволяет получить не истинный спектр 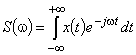 , а лишь его оценку (текущий спектр)
, а лишь его оценку (текущий спектр) 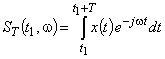 (зависит от
(зависит от 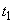 и
и 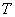 ). К сожалению, точность определения спектра связана с необходимостью знания самого точного спектра.
). К сожалению, точность определения спектра связана с необходимостью знания самого точного спектра.
Во многих случаях с приемлемой точностью возможна аппроксимация автокорреляционных функций экспоненциальными или экспоненциально-косинусными выражениями:
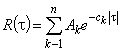 , (1)
, (1)
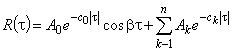 . (2)
. (2)
В этом случае спектральные плотности выражаются с помощью дробно-рациональной функции (соотношение двух полиномов, содержащих четные степени частоты 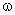 ). Если
). Если 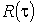 имеет вид (1), то спектральная плотность определяется формулой
имеет вид (1), то спектральная плотность определяется формулой
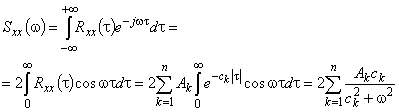 . (3)
. (3)
При аппроксимации вида (2):
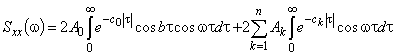 .
.
С учетом (3) второе слагаемое в выражении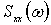 представляется в виде
представляется в виде 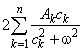 .
.
Что касается первого слагаемого, то справедливы следующие преобразования:
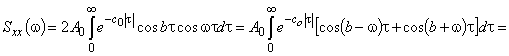
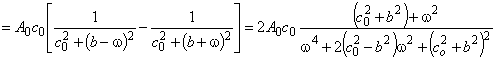 .
.
Таким образом, при аппроксимации автокорреляционной функции выражением вида (2) будем иметь
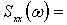
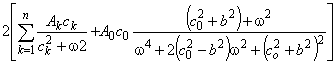 . (4)
. (4)
При аппроксимации автокорреляционной функции выражением (1) сначала выбирается такое положительное число 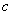 , чтобы функция
, чтобы функция 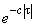 стремилась к нулю приблизительно с такой же скоростью, как и
стремилась к нулю приблизительно с такой же скоростью, как и 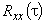 . Тогда, полагая в (1)
. Тогда, полагая в (1) 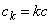 , получим
, получим
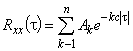 . (5)
. (5)
Для определения коэффициентов 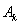 автокорреляционная функция представляется в виде
автокорреляционная функция представляется в виде
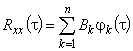 ; (6)
; (6)
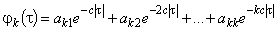 . (7)
. (7)
Коэффициенты 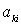 (
(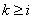 ) определятся из условий ортогональности -
) определятся из условий ортогональности -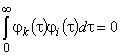 ,
, 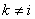 и нормированности —
и нормированности — 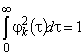 . Коэффициенты
. Коэффициенты 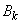 в выражении (6) определятся из условия минимума среднего квадрата ошибки аппроксимации
в выражении (6) определятся из условия минимума среднего квадрата ошибки аппроксимации
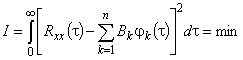 . (8)
. (8)
Приравнивая частные производные функционала (8) по коэффициентам 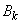 нулю, получим:
нулю, получим:
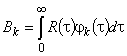
(учли ортогональность и нормированность системы функций 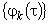 ).
).
Займемся аппроксимацией автокорреляционной функции выражением (2). Представим его в виде
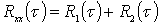 , (9)
, (9)
где
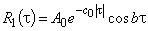 , (10)
, (10)
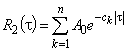 . (11)
. (11)
В первом приближении принимается
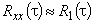
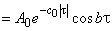 . (12)
. (12)
Коэффициенты 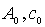 могут быть подобраны простыми методами, так как аппроксимация вида (12) является лишь первым приближением, которое затем уточняется. При подборе значений коэффициентов в выражении (12) используются соотношения:
могут быть подобраны простыми методами, так как аппроксимация вида (12) является лишь первым приближением, которое затем уточняется. При подборе значений коэффициентов в выражении (12) используются соотношения:
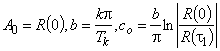 ,
,
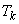 — точка, в которой автокорреляционная функция
— точка, в которой автокорреляционная функция 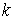 -й раз пересекает ась абсцисс (
-й раз пересекает ась абсцисс (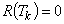 ),
), 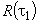 - значение первого отрицательного максимума автокорреляционной функции. Далее, введя
- значение первого отрицательного максимума автокорреляционной функции. Далее, введя
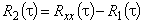 =
=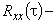
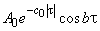 , (12)
, (12)
описанным выше методом получим ее аппроксимацию выражением вида (11).
Получили нижеуказанный алгоритм аппроксимации автокорреляционной функции стационарного случайного процесса экспоненциально-косинусным выражением (2).
1. Вычислить 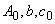 по формулам (4).
по формулам (4).
2. Вычислить дискретные значения 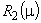 с шагом по времени
с шагом по времени 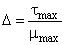 по формуле (6) при
по формуле (6) при 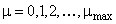 .
.
3. Выбрать параметр 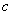 по поведению
по поведению 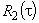 (по графику).
(по графику).
4. Выбрать число членов 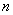 вида
вида 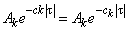 в выражении
в выражении 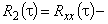
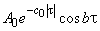 =
=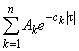 ,
,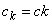 .
.
5. Вычислить 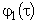 ,
,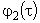 ,…,
,…,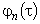 по формуле (7).
по формуле (7).
6. Вычислить 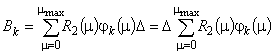 .
.
7. Вычислить 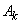 по формулам:
по формулам:
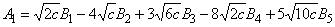 ,
,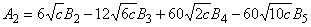 ,
,
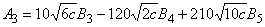 ,
,
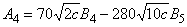 ,
,
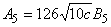 .
.
8. Вычислить дискретные значения 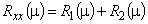 .
.
9. Вычислить дискретные значения спектральной плотности 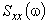 в диапазоне
в диапазоне 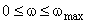 по формуле (4).
по формуле (4).
10. Если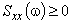 , аппроксимацию завершить. Если существует такое
, аппроксимацию завершить. Если существует такое 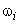 , что
, что 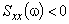 , то увеличить число членов
, то увеличить число членов 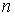 и повторить вычисления по пп.5–9.
и повторить вычисления по пп.5–9.
Приведенная методика прошла практическую апробацию при оценке работоспособности оборудования мобильных систем при ударе и сопровождающей вибрации [4,5], а также при разработке тренажных и обучающих комплексов для различных отраслей промышленности [6].
Литература:
1. Данилов А. М., Гарькина И. А., Домке Э. Р. Математическое и компьютерное моделирование сложных систем. — Пенза: ПГУАС. — 2011. — 296 с.
2. Будылина Е. А., Гарькина И. А., Данилов А. М. Моделирование с позиций управления в технических системах / Региональная архитектура и строительство. –2013. — № 2 (16). — С. 138–142.
3. Andreev A. N., Danilov A. M., Klyuev B. V., Lapshin E. V., Blinov A. V., Yurkov N. K. Information models for designing conceptual broad-profile flight simulators / Measurement Techniques. August 2000. — Vol.43. Issue 8. — P.667–672.
4. Данилов А. М., Гарькина И. А., Гарькин И. Н. Защита от удара и сопровождающей вибрации: экспоненциально-тригонометрическая аппроксимация функций / Региональная архитектура и строительство. — 2012. –№ 3(14). — С.85–89.
5. Гарькина И. А., Гарькин И. Н. Идентификация и аппроксимация колебаний конструктивных элементов / Молодой ученый. –2013. -№ 3(50). — С.44–48.
6. Еремкин А. И., Прошин А. П., Данилов А. М., Гарькина И. А. Промышленные и аэрокосмические приложения системных методологий, идентификации систем и теории управления / Наука и технологии. Избранные труды. — М.: РАН. — 2005. — С.556–567.

