Рассмотрим актуальные для разработки тренажных и обучающих комплексов вопросы определения структуры оценки управляющих воздействий оператора в сложной эргатической системе [1]. С учетом простоты и получения приемлемой точности описания управляющих воздействий оператора представим обобщенный вектор управления [2…5], состоящим из компонент:
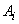 — амплитуда импульсов управления;
— амплитуда импульсов управления;
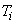 — длительность импульсов;
— длительность импульсов;
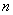 — число импульсов при заданной длительности реализаций
— число импульсов при заданной длительности реализаций 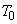 .
.
Для иллюстрации приведем вероятности амплитуд и длительностей импульсов управляющих воздействий для транспортного самолета, полученные в результате статистической обработки как случайных функций приводятся на рис.1.
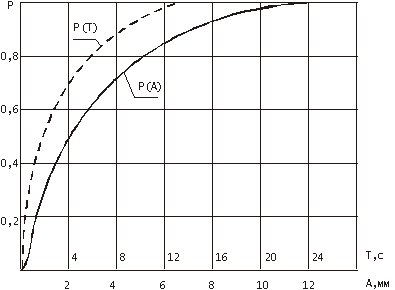
Рис. 1. Вероятности амплитуды и длительностей импульсных управляющих движений оператора
Предполагается справедливость известной гипотезы Милсама и Миллера об импульсном характере управления человека-оператора. При фиксированной длительности 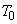 реализации, чем больше
реализации, чем больше 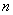 , тем, очевидно, выше активность и соответственно психофизиологическая напряженность оператора [6]. Ясно, что активность человека-оператора не может быть нулевой (оператор в процессе управления не только действует в импульсном режиме, но и опрашивает объект в процессе управления); она не может быть и бесконечной. Поэтому нормированное значение
, тем, очевидно, выше активность и соответственно психофизиологическая напряженность оператора [6]. Ясно, что активность человека-оператора не может быть нулевой (оператор в процессе управления не только действует в импульсном режиме, но и опрашивает объект в процессе управления); она не может быть и бесконечной. Поэтому нормированное значение 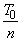 (нормировку можно производить делением на среднее квадратичное отклонение) должно принадлежать некоторому оптимальному интервалу. Если полагать, что весовые константы аддитивного глобального критерия качества все положительны, то из сказанного вытекает, что частными критериями качества целесообразно принять как нормированные значения
(нормировку можно производить делением на среднее квадратичное отклонение) должно принадлежать некоторому оптимальному интервалу. Если полагать, что весовые константы аддитивного глобального критерия качества все положительны, то из сказанного вытекает, что частными критериями качества целесообразно принять как нормированные значения 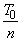 , так и
, так и 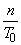 (будут ограничены как сверху, так и снизу; их оптимальные значения зависят от заданной длительности
(будут ограничены как сверху, так и снизу; их оптимальные значения зависят от заданной длительности 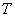 ).
).
Энергетические затраты (определяются величиной;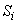 — площадь
— площадь 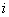 -го импульса) на стабилизацию программного управления должны быть минимальными. Строго говоря, они должны быть оптимальными: при очень малых затратах система будет «вялой», а слишком большие затраты также недопустимы. Если учесть, что
-го импульса) на стабилизацию программного управления должны быть минимальными. Строго говоря, они должны быть оптимальными: при очень малых затратах система будет «вялой», а слишком большие затраты также недопустимы. Если учесть, что
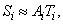
то из этого аналогично предыдущему следует необходимость включения в число частных критериев значений 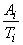 (нормированных и при положительных безразмерных весовых константах!). В известном смысле
(нормированных и при положительных безразмерных весовых константах!). В известном смысле 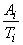 характеризует перегрузки в системе. Поэтому в первом приближении можно ограничиться включением в число частных критериев нормированную величину
характеризует перегрузки в системе. Поэтому в первом приближении можно ограничиться включением в число частных критериев нормированную величину 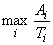 .
.
Таким образом, предлагаемый функционал качества системы будет иметь вид:
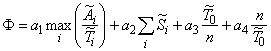 ; (
; (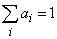 ; ~ — знак нормировки).
; ~ — знак нормировки).
Выбор весовых констант легко осуществляется по степени корреляционных связей между 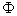 и частными критериями качества (в первом приближении весовые константы можно принять одинаковыми). Функционал не претендует на полноту; его можно уточнить, введя дополнительные частные критерии.
и частными критериями качества (в первом приближении весовые константы можно принять одинаковыми). Функционал не претендует на полноту; его можно уточнить, введя дополнительные частные критерии.
Из приведенного естественным образом вытекает необходимость в критериях, более полно характеризующих управляющие действия оператора. В частности, позволяющие определить:
- качество выполнения задания (вне зависимости от состояния системы после выполнения задания);
- затраты энергоресурсов системы на выполнение задания;
- четкость действий оператора (минимум лишних воздействий на систему при выполнении задания).
Формализация оценки первого фактора в общем случае затруднительна. Это можно сделать лишь очень грубо по двухбалльной системе: задание выполнено; задание не выполнено. Возможен учет и некоторых специфических особенностей для получения более дифференцируемой оценки. Поэтому качество управления можно оценивать лишь при выполнении задания (в этом случае вычисляется величина критерия качества для соответствующего управления). Для целей обучения важно именно выполнение задания при рациональном использовании систем (превалирующую роль играют затраты энергоресурсов системы на выполнение задания; важна и выработка у оператора четкого навыка работы с системой). Так что, при разработке критерия качества управления (при выполнении задания) основное внимание должно уделяться второму и третьему факторам. Количественная оценка затрат энергоресурсов системы при этом может оцениваться по функционалу
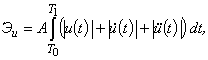
(предполагается возможность вычисления управляющих воздействий 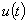 в любой момент времени
в любой момент времени 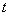 на интервале
на интервале 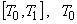 — время начала,
— время начала, 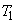 — время окончания выполнения задания,
— время окончания выполнения задания,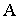 - некоторый нормирующий множитель). Величина
- некоторый нормирующий множитель). Величина 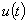 характеризует энергетические затраты, a
характеризует энергетические затраты, a 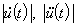 — возникающие в системе динамические нагрузки при воздействиях оператора.
— возникающие в системе динамические нагрузки при воздействиях оператора.
Нечеткость действий оператора определяется (как лишние воздействия на систему) вполне можно оценить функционалом
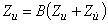
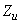 — длина кривой
— длина кривой 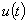 на интервале
на интервале 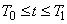 ,
, 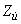 — длина кривой
— длина кривой 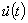 ,
,
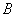 — нормирующий множитель. Функционал
— нормирующий множитель. Функционал 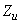 характеризует и затраты ресурсов системы с учетом длительности выполнения задания:
характеризует и затраты ресурсов системы с учетом длительности выполнения задания:
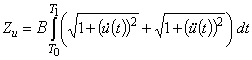
или
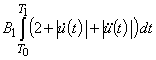
(следует из 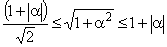 ).
).
Из приведенного выше обобщенный критерий качества управления определится в виде:
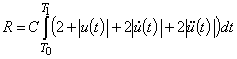
или
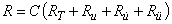 ;
;
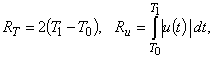
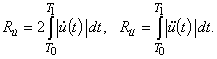
Выбор нормирующего множителя C осуществлялся из условия, чтобы для хорошо обученных операторов значение 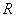 находилось в интервале от 0 до 4 (
находилось в интервале от 0 до 4 (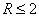 — для операторов 1-го класса,
— для операторов 1-го класса, 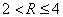 - для операторов 2-го класса). При дискретном задании управления
- для операторов 2-го класса). При дискретном задании управления 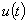 с шагом
с шагом 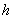 (на практике
(на практике 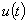 может быть задано графически; в этом случае, снимая значения
может быть задано графически; в этом случае, снимая значения 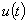 , следует учесть масштаб и, возможно, изменить нормирующий множитель C) получим:
, следует учесть масштаб и, возможно, изменить нормирующий множитель C) получим:
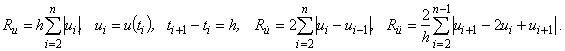
В функционале 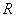 компонента
компонента 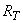 характеризует длительность выполнения задания;
характеризует длительность выполнения задания; 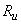 — затрату энергии системы на выполнение задания;
— затрату энергии системы на выполнение задания; 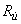 — колебания в системе;
— колебания в системе; 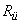 — динамические перегрузки.
— динамические перегрузки.
Зависимости областей равных оценок от технических характеристик объекта управления, математическое моделирование управляющих движений летчика при оценке пилотажных свойств по другим векторным критериям уже подробно рассматривались в [7…9].
Литература:
1. Данилов А. М., Гарькина И. А. Сложные системы: идентификация, синтез, управление: монография. — Пенза: ПГУАС, 2011. — 308 с.
2. A. N. Andreev, A. M. Danilov, B. V. Klyuev, E. V. Lapshin, A. V. Blinov, N. K. Yurkov. Information models for designing conceptual broad-profile flight simulators / Measurement Techniques. August 2000. — Vol.43. Issue 8. — P.667–672.
3. Гарькина И. А., Данилов А. М., Пылайкин С. А. Транспортные эргатические системы: информационные модели и управление / Мир транспорта и технологических машин. — 2013. — № 1 (40). — С. 115–122.
4. Родионов Ю. В., Ветохин А. С. Динамический автотренажер / Мир транспорта и технологических машин. — 2011. — № 4. –С.90–93.
5. Данилов А. М.,Гарькина И. А., Домке Э. Р. Математическое и компьютерное моделирование сложных систем. — Пенза: ПГУАС, 2011. — 296 с.
6. Будылина Е. А., Гарькина И. А., Данилов А. М. Моделирование с позиций управления в технических системах / Региональная архитектура и строительство. –2013. — № 2 (16). — С. 138–142.
7. Гарькина И. А., Данилов А. М. Управление в сложных технических системах: методологические принципы управления / Региональная архитектура и строительство. –2012. — № 1 (12). — С.39–43.
8. Будылина Е. А.,Гарькина И. А., Данилов А. М. Приближенные методы декомпозиции при настройке имитаторов динамических систем / Региональная архитектура и строительство. — 2013. — № 3(17). — C. 150–156.
9. Будылина Е. А.,Гарькина И. А., Данилов А. М., Пылайкин С. А. Управление безопасностью сложных систем / Молодой ученый. — 2013. –№ 11(58). — С.78–81.

